Corriente y campo magnético de dos hilos
De Laplace
Contenido |
1 Enunciado
Se tienen dos hilos de cobre de gran longitud 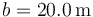 . Uno de ellos tiene un diámetro
. Uno de ellos tiene un diámetro 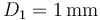 y el otro
y el otro 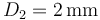 . Se sitúan paralelamente a una distancia
. Se sitúan paralelamente a una distancia 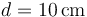 y se conectan sus extremos de forma que constituyen una asociación en paralelo. Entre los extremos de la asociación se aplica una diferencia de potencial
y se conectan sus extremos de forma que constituyen una asociación en paralelo. Entre los extremos de la asociación se aplica una diferencia de potencial 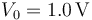 .
.
- Calcule la intensidad de corriente que circula por cada uno de los hilos.
- ¿Cuál es la potencia total disipada en el sistema?
- Halle el vector campo magnético producido por los hilos en el punto O, centro del sistema.
- Empleando los ejes de la figura, ¿en qué punto del eje OX se anula el campo magnético?
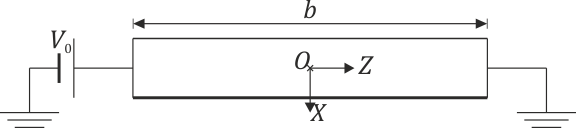
Dato: Conductividad del cobre, 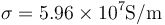 ; permeabilidad del vacío
; permeabilidad del vacío 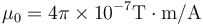 ; campo magnético creado por un hilo infinito, expresado en cilíndricas,
; campo magnético creado por un hilo infinito, expresado en cilíndricas,
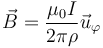
2 Intensidades de corriente
Cada uno de los hilos está conectado a la misma diferencia de potencial, por lo que la corriente que circula por cada uno la da la ley de Ohm

siendo la resistencia de cada hilo
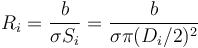
Para el hilo de 1mm de diámetro
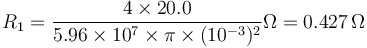
Para el hilo de 2mm, la sección será el cuádruple y la resistencia la cuarta parte
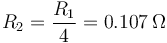
La intensidad de corriente que circula por el primer hilo vale

y para el hilo 2, que tiene un cuarto de esta resistencia resulta el cuadruple de intensidad

3 Potencia disipada
La potencia disipada en cada hilo es de la forma

y la total es la suma de las dos
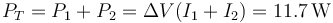
4 Campo magnético en el centro
El punto donde queremos hallar el campo está muy próximo a los hilos, en comparación con la longitud de estos. Por ello, podemos usar la fórmula para un hilo infinitamente largo, que nos dará una buena aproximación al campo real.
La fórmula para el campo de un solo hilo es
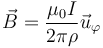
donde ρ es la distancia al hilo (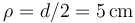 para los dos hilos) y
para los dos hilos) y 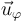 es el unitario en la dirección acimutal, que da vueltas en torno al hilo según la regla de la mano derecha.
es el unitario en la dirección acimutal, que da vueltas en torno al hilo según la regla de la mano derecha.
Para el hilo superior este vector equivale a 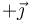 en el punto O, ya que ahí la dirección acimutal va hacia adentro, que es el sentido del eje Y. Para el hilo inferior el campo sale hacia afuera, es decir va en el sentido de
en el punto O, ya que ahí la dirección acimutal va hacia adentro, que es el sentido del eje Y. Para el hilo inferior el campo sale hacia afuera, es decir va en el sentido de 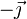
Por tanto tenemos
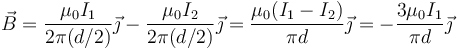
con el valor numérico
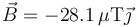
En el punto O el campo viene hacia afuera del plano que, como hemos dicho, es el sentido de 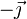 .
.
5 Campo magnético nulo
Tal como se ve en el apartado anterior, en la zona central los campos magnéticos de los dos hilos van en sentidos opuestos. Si nos acercamos al hilo 1 (el de menor intensidad) su campo magnético aumenta, y el del 2 disminuye. A la distancia adecuada uno anula al otro.
El campo en cualquier punto del plano de los hilos, entre ellos, vale

Puesto que I2 = 4I1 para que el campo se anula debe ser
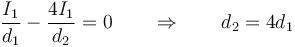
y como
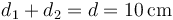
queda

En términos de los ejes de la figura