Campo magnético creado por corrientes (GIE)

De Laplace

Contenido

1 Introducción
2 Campo producido por una carga en movimiento
3 Campo creado por una distribución de corriente
- 3.1 Ley de Biot y Savart
- 3.2 Fuerza entre corrientes
4 Campos de corrientes lineales

1 Introducción

Al estudiar la ley de Lorentz se describe la acción que un campo magnético produce sobre una carga en movimiento o un conjunto de ellas. La siguiente cuestión es quién produce dicho campo magnético.

De acuerdo con la simetría establecida por Ampère, del mismo modo que las cargas en movimiento experimentan el campo magnético, también son su causa.

La corrientes eléctricas, no obstante, no son la única causa de campo magnético; los dipolos magnéticos inherentes a cada partícula, también generan campos magnéticos.

2 Campo producido por una carga en movimiento

2.1 Expresión del campo

Para una carga puntual que se encuentra instantáneamente en el punto 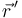$\vec{r}^{\,\prime}$ moviéndose con velocidad instantánea 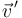$\vec{v}^{\,\prime}$ , mucho menor que la de la luz, el campo magnético que produce en todos los puntos del espacio vale

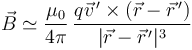
$\vec{B}\simeq \frac{\mu_0}{4\pi}\,\frac{q\vec{v}^{\,\prime}\times(\vec{r}-\vec{r}^{\,\prime})}{|\vec{r}-\vec{r}^{\,\prime}|^3}$

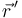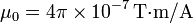siendo $\vec{r}^{\,\prime}$ la posición instantánea de la carga. $μ 0$ es una constante denominada permeabilidad del vacío, cuyo valor en el SI es $\mu_0=4\pi\times 10^{-7}\,\mathrm{T}{\cdot}\mathrm{m}/\mathrm{A}$ .

Si expresamos este campo en coordenadas cilíndricas, tomando el origen en la propia carga y el eje Z en la dirección de la velocidad nos queda la expresión

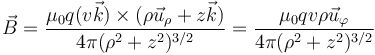
$\vec{B}=\frac{\mu_0 q(v\vec{k})\times(\rho\vec{u}_\rho+z\vec{k})}{4\pi(\rho^2+z^2)^{3/2}}=\frac{\mu_0qv\rho\vec{u}_\varphi}{4\pi(\rho^2+z^2)^{3/2}}$

Las líneas del campo magnético de una carga en movimiento son circunferencias en torno al movimiento de la carga, ya que el campo va en la dirección acimutal. En los puntos del eje (salvo en la propia carga) este campo es nulo (ya que $ρ = 0$ ).

2.2 El magnetismo y la 3ª ley de Newton

Combinando la ecuación anterior con la ley de Lorentz resulta para la fuerza magnética que la carga 1 (en movimiento) produce sobre la 2 (también en movimiento) la expresión

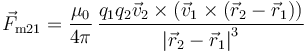
$\vec{F}_{\mathrm{m}21} = \frac{\mu _0}{4\pi}\,\frac{q_1q_2\vec{v}_2 \times \left(\vec{v}_1 \times \left(\vec{r}_2 - \vec{r}_1 \right) \right)}{\left|\vec{r}_2 - \vec{r}_1 \right|^3}$

Esta fuerza es extraña porque no verifica el principio de acción y reacción

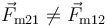
$\vec{F}_{\mathrm{m}21} \neq \vec{F}_{\mathrm{m}12}$

Un caso sencillo en el que esto ocurre es el de dos cargas moviéndose en direcciones perpendiculares.

La 3ª ley de Newton es necesaria para que se conserve la cantidad de movimiento, 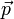$\vec{p}$ . Si las fuerzas no se anulan exactamente

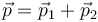
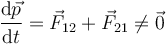
$\vec{p}=\vec{p}_1+\vec{p}_2\,$ $\Rightarrow$ $\Rightarrow$ $\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}_{12}+\vec{F}_{21}\neq\vec{0}$

La conservación de la cantidad de movimiento (como la de la energía, que también depende de esta ley) es uno de los puntales de la Física. ¿Cómo se resuelve este conflicto? Considerando una cantidad de movimiento total, que además de incluir las dos partículas, incorpora una contribución del campo electromagnético 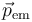$\vec{p}_\mathrm{em}$ , de forma que

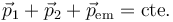
$\vec{p}_1+\vec{p}_2+\vec{p}_\mathrm{em}=\mathrm{cte.}$

De esta forma, el campo se lleva toda la cantidad de movimiento que pierde el sistema mecánico (o aporta la que gana).

Esto implica que el campo electromagnético, además de almacenar una energía, almacena una cantidad de movimiento (y un momento angular, ya puestos), que son propiedades usualmente asignadas a las partículas. Por ello, en una descripción completa, el campo electromagnético tiene tanta realidad como las propias partículas. En mecánica cuántica, estas propiedades se le asignan a una partícula que representa al campo electromagnético: el fotón.

En el caso de que se trate del campo magnético de corrientes estacionarias sí se cumple la 3ª ley de Newton, sin necesidad de términos adicionales

2.3 Fuerza entre dos cargas en movimiento paralelo

Supongamos dos cargas $q 1$ y $q 2$ que se mueven paralelamente con la misma velocidad 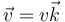$\vec{v} = v\vec{k}$ sobre rectas separadas una distancia 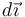$d\vec{\imath}$ . El campo de la 1ª en la posición de la 2ª es

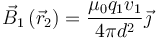
$\vec{B}_1\left(\vec{r}_2\right) = \frac{\mu _0q_1v_1}{4\pi d^2}\vec{\jmath}$

La fuerza magnética sobre $q 2$ es

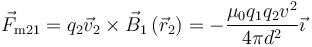
$\vec{F}_{\mathrm{m}21} = q_2\vec{v}_2 \times \vec{B}_1\left(\vec{r}_2\right) = - \frac{\mu _0q_1q_2v^2}{4\pi d^2}\vec{\imath}$

La fuerza magnética es atractiva si las cargas son del mismo signo.

Podemos comparar la magnitud de esta fuerza con la fuerza eléctrica entre ambas cargas. Si la velocidad de las cargas es pequeña, podemos aproximar la fuerza mediante la ley de Coulomb:

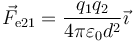
$\vec{F}_{\mathrm{e}21} = \frac{q_1q_2}{4\pi\varepsilon_0d^2}\vec{\imath}$

La proporción entre ambas fuerzas es

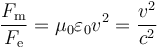
$\frac{F_\mathrm{m}}{F_\mathrm{e}}=\mu_0\varepsilon_0 v^2=\frac{v^2}{c^2}$

donde 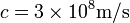$c = 3\times 10^{8}\mathrm{m}/\mathrm{s}$ es la velocidad de la luz. Por ello, normalmente

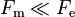
$F_\mathrm{m}\ll F_\mathrm{e}$

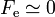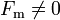Las fuerzas magnéticas sólo son apreciables porque la materia es neutra. En la interacción entre dos hilos conductores de corriente, las fuerzas eléctricas entre iones y electrones se cancelan (y $F_\mathrm{e}\simeq 0$ ). Para la fuerza magnética sólo cuentan los electrones móviles, y $F_\mathrm{m}\neq 0$ .

Una observación más sobre esta fuerza magnética y su relación con la eléctrica. Al hablar del campo magnético producido por una carga puntual se introduce su velocidad, y en la fuerza de Lorentz aparece otra velocidad. la pregunta inmediata es ¿velocidad respecto a qué? No es la velocidad relativa de una carga respecto a la otra (ya que en este ejemplo, las dos cargas se mueven del mismo modo), sino la velocidad respecto a un sistema de referencia fijo. Ahora bien, una de las enseñanzas de la teoría de la relatividad es que no existen los sistemas de referencia absolutos. Si cambiamos de sistema de referencia absoluto resulta que la fuerza magnética valdrá más o menos o incluso anularse. Este comportamiento claramente no relativista de la fuerza magnética no puede ser correcto.

La expresión correcta de la fuerza electromagnética requiere meterse en las honduras de la relatividad especial, por lo que sólo indicaremos dos detalles:

Lo que tiene significado es la fuerza total, suma de la fuerza magnética y de la eléctrica

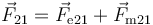
$\vec{F}_{21}=\vec{F}_{\mathrm{e}21}+\vec{F}_{\mathrm{m}21}$

La fuerza eléctrica también depende de la velocidad de las cargas (la ley de Coulomb es solo una aproximación), de forma que al cambiar de sistema de referencia no solo cambia la fuerza magnética, sino también la eléctrica (en una cantidad similar), de manera que la resultante sí se transforma como debe hacerlo una fuerza relativista.

3 Campo creado por una distribución de corriente

3.1 Ley de Biot y Savart

Sumando las contribuciones de los campos creados por cada una de las cargas individuales, resulta la expresión para el campo creado por una distribución de cargas puntuales

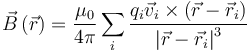
$\vec{B}\left(\vec{r}\right) = \frac{\mu _0}{4\pi}\sum_i \frac{q_i\vec{v}_i \times \left(\vec{r} - \vec{r}_i\right)}{\left| \vec{r} - \vec{r}_i\right|^3}$

A partir de aquí se obtiene el campo debido a una corriente lineal, sumando las contribuciones de las cargas que la forman

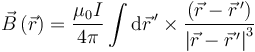
$\vec{B}\left(\vec{r}\right) = \frac{\mu _0I}{4\pi}\int\mathrm{d}\vec{r}^{\,\prime}\times\frac{\left(\vec{r} - \vec{r}^{\,\prime}\right)}{\left|\vec{r} - \vec{r}^{\,\prime}\right|^3}$

Esta expresión se denomina Ley de Biot y Savart

3.2 Fuerza entre corrientes

Dadas dos distribuciones lineales, la fuerza entre ellas será:

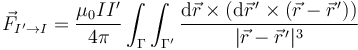
$\vec{F}_{I'\to I}=\frac{\mu_0II'}{4\pi}\int_{\Gamma}\int_{\Gamma'}\frac{\mathrm{d}\vec{r}\times(\mathrm{d}\vec{r}^{\,\prime}\times(\vec{r}-\vec{r}^{\,\prime}))}{|\vec{r}-\vec{r}^{\,\prime}|^3}$

Esta fórmula también se conoce como Ley de Biot y Savart. Predice que corrientes paralelas (↑↑) se atraen, mientras que las antiparalelas (↑↓) se repelen.

4 Campos de corrientes lineales

4.1 Campo de una espira circular

Supongamos una espira circular por la cual circula una corriente $I$ . Se trata de hallar el campo magnético en los puntos del eje de la espira (para el resto del espacio no existe expresión analítica sencilla)

Aplicando la ley de Biot y Savart

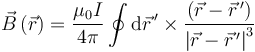
$\vec{B}\left(\vec{r}\right) = \frac{\mu _0I}{4\pi}\oint\mathrm{d}\vec{r}^{\,\prime}\times\frac{\left(\vec{r} - \vec{r}^{\,\prime}\right)}{\left|\vec{r} - \vec{r}^{\,\prime}\right|^3}$

Tomamos como eje z el de la espira, las integrales para $B x$ y $B y$ se anulan, lo que se puede explicar como que el campo horizontal de un segmento de espira se anula con el del diametralmente opuesto.

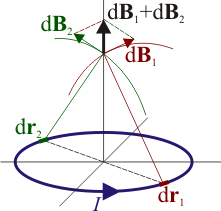
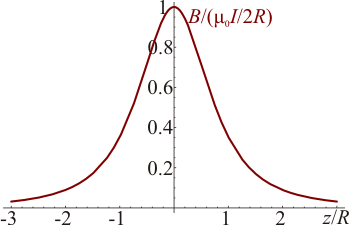
La componente z del campo producido por un diferencial de corriente se obtiene proyectando

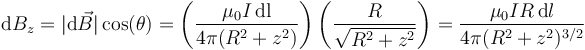
$\mathrm{d}B_z = |\mathrm{d}\vec{B}|\cos(\theta) = \left(\frac{\mu_0I\,\mathrm{dl}}{4\pi (R^2+z^2)}\right)\left(\frac{R}{\sqrt{R^2+z^2}}\right)=\frac{\mu_0IR\,\mathrm{d}l}{4\pi(R^2+z^2)^{3/2}}$

Al sumar para toda la espira simplemente debemos integrar $d l$ , que da $2π R$ y nos da el campo total en los puntos de la espira:

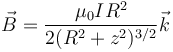
$\vec{B}=\frac{\mu_0IR^2}{2(R^2+z^2)^{3/2}}\vec{k}$

Este campo va en la dirección del eje y su gráfica es una campana con un máximo en el centro.

El valor máximo del campo es $B max = μ 0 I / 2 R$ , que para una espira de 10 cm por la cual circule una corriente de 1 A da un campo 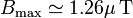$B_\mathrm{max} \simeq 1.26\mu\,\mathrm{T}$ .

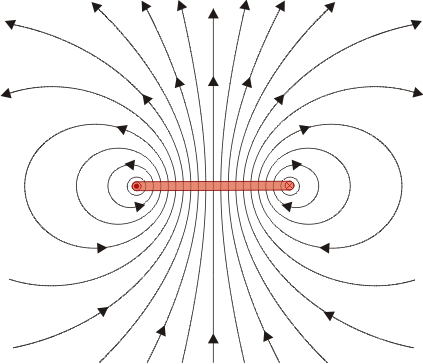
En el resto del espacio el campo se puede calcular de forma numérica, resultando líneas cerradas alrededor de la espira. Las líneas están en planos 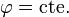$\varphi=\mathrm{cte.}$ . La distribución de líneas posee simetría acimutal.

Las líneas de campo salen por la cara superior (definida según la regla de la mano derecha) y entran por la cara inferior.

4.2 Campo de un solenoide finito

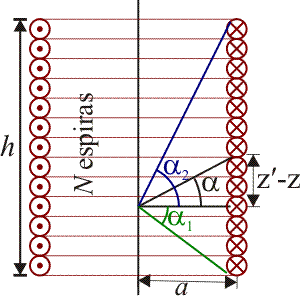
Un solenoide, o bobina, consiste en un hilo arrollado de forma helicoidal sobre un cilindro de radio $a$ y longitud $h$ . Una bobina es un solo hilo por el cual circula una corriente $I$ , pero si el paso de rosca es pequeño, puede aproximarse por un conjunto de N espiras circulares apiladas.

En los puntos del eje del solenoide, el campo magnético será la suma de los de las espiras que lo forman, teniendo en cuenta que cada una se encuentra a diferente altura $z i$

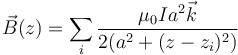
$\vec{B}(z) = \sum_i \frac{\mu_0Ia^2\vec{k}}{2(a^2+(z-z_i)^2)}$

Este sumatorio es poco práctico, porque usualmente contiene varios centenares de términos (no obstante, es fácil de implementar por ordenador).

Para hallar el valor aproximado de la suma, la sustituimos por una integral. Definimos la densidad de espiras como el número de vueltas por unidad de longitud

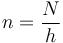
$n = \frac{N}{h}$

Si consideramos una bobina densa, en la que apenas hay espacio entre vuelta y vuelta, en una pequeña distancia $d z'$ alrededor del punto $z'$ se encuentra el número de vueltas

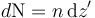
$d\mathrm{N} = n\,\mathrm{d}z'$

Todas estas vueltas se pueden considerar a la misma altura, lo que nos deja con la integral

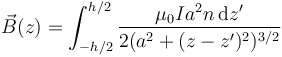
$\vec{B}(z) = \int_{-h/2}^{h/2}\frac{\mu_0Ia^2n\,\mathrm{d}z'}{2(a^2+(z-z')^2)^{3/2}}$

Esta integral se resuelve con el cambio de variable

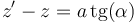
$z' - z = a\,\mathrm{tg}(\alpha)$

y queda el campo

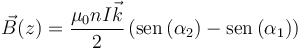
$\vec{B}(z)=\frac{\mu_0nI\vec{k}}{2}\left(\mathrm{sen}\,(\alpha_2)-\mathrm{sen}\,(\alpha_1)\right)$

siendo $α 1$ y $α 2$ los ángulos con los que se ven los extremos inicial y final de la bobina, respectivamente.

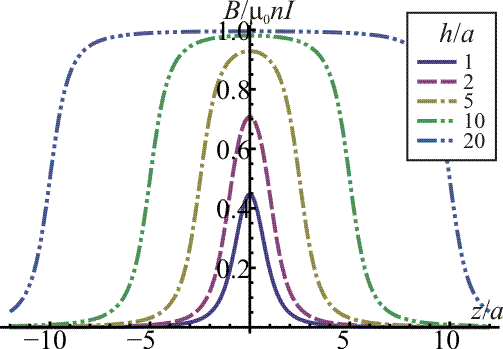
Este campo, como función de z posee forma de campana, cada vez más plana a medida que aumenta la longitud del cilindro. En el límite 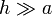$h\gg a$ resulta un campo constante:

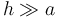
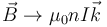
$h\gg a\,$ $\Rightarrow$ $\alpha_1\to-\frac{\pi}{2}\qquad \alpha_2\to+\frac{\pi}{2}$ $\Rightarrow$ $\vec{B}\to\mu_0nI\vec{k}$

Este campo posee la propiedad de que no depende del radio de la bobina, con tal que 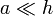$a\ll h$ . Puede demostrarse asimismo que, para bobinas infinitamente largas, este campo tiene el mismo valor en todos los puntos del interior, no solo los del eje.

4.3 Campo de una corriente rectilínea

4.3.1 Caso de un segmento

Un segmento rectilíneo de longitud $h$ por el cual circula una intensidad de corriente $I$ equivale a un conjunto de cargas moviéndose con la velocidad de arrastre promedio. El campo magnético resultante es la suma del campo de cada una, pero teniendo en cuenta que cada una se halla en una posición diferente.

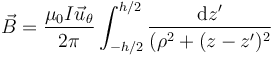
$\vec{B}=\frac{\mu_0I\vec{u}_\theta}{2\pi}\int_{-h/2}^{h/2}\frac{\mathrm{d}z'}{(\rho^2+(z-z')^2}$

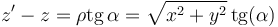
Esta integral se resuelve mediante el cambio de variable $z'-z = \rho\mathrm{tg}\,\alpha=\sqrt{x^2+y^2}\,\mathrm{tg}(\alpha)$

$α$ es el ángulo con el que se ve un punto cualquiera del segmento desde el punto donde queremos hallar el campo. Sean $α 1$ y $α 2$ los ángulos con que se ven los extremos del segmento.

La solución es

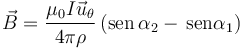
$\vec{B} = \frac{\mu _0I\vec{u}_\theta}{4\pi \rho}\left(\mathrm{sen}\,{\alpha _2} - \,\mathrm{sen}{\alpha _1}\right)$

De la expresión en cilíndricas se ve que las líneas de campo magnético dan vueltas en torno al eje del segmento, según la regla de la mano derecha.

A la hora de calcular el campo producido por ejemplo por una espira poligonal, no podemos fijar simultáneamente el eje Z sobre todos los lados a la vez, por lo que debemos reinterpretar la expresión para el campo de una forma más general.

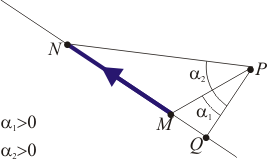
Nuestro punto de partida es el campo magnético medido en un punto $P$ , debido a un segmento rectilíneo de extremos $M$ y $N$ , dado por

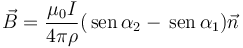
$\vec{B}=\frac{\mu_0 I}{4\pi\rho}(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1)\vec{n}$

donde

ρ

debe entenderse como la distancia desde el punto donde se quiere medir el campo a la recta soporte del segmento, esto es, la distancia PQ medida sobre la perpendicular, siendo Q el punto de la recta más cercano a P. Q no tiene por qué pertenecer al segmento.

α 1

y

α 2

son los ángulos que esta perpendicular PQ forma con las líneas PM y PN. Estos ángulos tienen signo, positivo si PM queda por delante de PQ (según el sentido de la corriente) y negativo si queda por detrás. Lo mismo para el ángulo

α 1

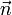. Por último, $\vec{n}$ representa un vector normal al plano definido por P, M y N, con sentido el dado por la regla de la mano derecha respecto a la corriente que circula por el segmento (irá hacia afuera de la pantalla si P se encuentra a la izquierda del segmento y hacia adentro si está a la derecha).

4.3.2 Caso de un hilo infinito

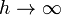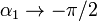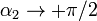De la expresión para un segmento se deduce el campo para un hilo infinitamente largo. Si $h\to\infty$ , los ángulos extremos tienen los límites $\alpha_1\to-\pi/2$ , $\alpha_2\to+\pi/2$ y el campo

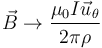
$\vec{B} \to \frac{\mu _0I\vec{u}_\theta}{2\pi \rho}$

Este campo decae con la distancia al hilo como $1 / ρ$ (a doble distancia mitad de campo). En cartesianas, este campo se escribe

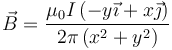
$\vec{B}=\frac{\mu _0I\left(-y\vec{\imath} + x\vec{\jmath}\right)}{2\pi \left(x^2 + y^2\right)}$

Si tenemos dos o más hilos paralelos se suman sus expresiones en cartesianas (no en cilíndricas)

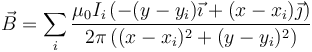
$\vec{B} =\sum_i \frac{\mu _0I_i\left(-(y-y_i)\vec{\imath} + (x-x_i)\vec{\jmath}\right)}{2\pi \left((x-x_i)^2 + (y-y_i)^2\right)}$

con $x i, y i$ , las posiciones de cada hilo en el plano XY.

4.3.3 Fuerza entre dos hilos. El Amperio

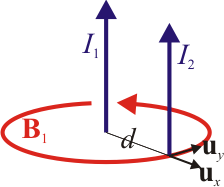
Supongamos dos hilos paralelos separados una distancia $d$ , por los cuales circulan corrientes $I 1$ e $I 2$ . La fuerza que el hilo 1 ejerce sobre el 2 es

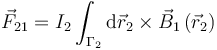
$\vec{F}_{21} = I_2\int_{\Gamma _2} \mathrm{d}\vec{r}_2 \times \vec{B}_1\left(\vec{r}_2\right)$

$\vec{B}_1(\vec{r}_2)$ vale, en todos los puntos de $Γ 2$

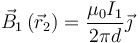
$\vec{B}_1\left(\vec{r}_2\right) = \frac{\mu_0I_1}{2\pi d}\vec{\jmath}$

La fuerza sobre un tramo de longitud $L$ es

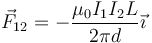
$\vec{F}_{12}= -\frac{\mu_0I_1I_2L}{2\pi d}\vec{\imath}$

Este resultado se emplea para definir el amperio:

Es la corriente que al circular por dos hilos rectilíneos paralelos, de longitud infinita y sección circular despreciable separados 1 m en el vacío, produce una fuerza por unidad de longitud igual a 2×10^-7N/m

4.4 La doble regla de la mano derecha

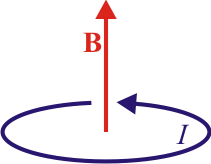
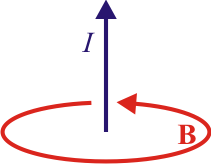
De los ejemplos anteriores y del campo de una carga puntual puede verse que el campo magnético creado por una corriente lineal cumple la regla de la mano derecha por partida doble:

El campo respecto a la corriente
La corriente respecto al campo

Campo magnético creado por corrientes (GIE)

De Laplace

Contenido

1 Introducción

2 Campo producido por una carga en movimiento

2.1 Expresión del campo

2.2 El magnetismo y la 3ª ley de Newton

2.3 Fuerza entre dos cargas en movimiento paralelo

3 Campo creado por una distribución de corriente

3.1 Ley de Biot y Savart

3.2 Fuerza entre corrientes

4 Campos de corrientes lineales

4.1 Campo de una espira circular

4.2 Campo de un solenoide finito

4.3 Campo de una corriente rectilínea

4.3.1 Caso de un segmento

4.3.2 Caso de un hilo infinito

4.3.3 Fuerza entre dos hilos. El Amperio

4.4 La doble regla de la mano derecha

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES