Problemas de mecánica analítica (CMR)
De Laplace
(→Péndulo compuesto) |
(→Dos rodillos unidos por un resorte) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | ==[[Estudio analítico de máquina de Atwood]]== | ||
| + | Una máquina de Atwood está formada por dos masas <math>m_1</math> y <math>m_2</math> unidas por un hilo ideal, inextensible y sin masa, que pasa por una polea ideal, sin rozamiento y sin masa. | ||
| + | # Empleando el principio de D’Alembert halle la aceleración de cada una de las masas. | ||
| + | # Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea. | ||
| + | # Suponga ahora que la polea es un disco de radio <math>R</math> con momento de inercia <math>I</math>. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda? | ||
| + | |||
| + | ==[[Estudio analítico del plano inclinado]]== | ||
| + | Una partícula de masa <math>m</math> desliza sin rozamiento por un plano inclinado, de base <math>b</math> y altura <math>h</math>, sometida a la fuerza de la gravedad y las fuerzas de reacción. Empleando como coordenadas las cartesianas de la partícula con el eje OX horizontal y el OY vertical: | ||
| + | # Escriba la ecuación del vínculo entre las coordenadas. | ||
| + | # A partir del principio de D’Alembert, obtenga las componentes de la aceleración de la masa. | ||
| + | # Con ayuda de los multiplicadores de Lagrange, halle las componentes de la fuerza de reacción del plano sobre la masa. | ||
| + | |||
| + | ==[[Estudio analítico del péndulo simple]]== | ||
| + | Empleando el principio de D’Alembert, obtenga las ecuaciones de movimiento para las coordenadas cartesianas de un péndulo simple que oscila verticalmente. | ||
| + | |||
==[[Estudio analítico de dos masas unidas por un muelle]]== | ==[[Estudio analítico de dos masas unidas por un muelle]]== | ||
Como en el problema “[[Dos masas unidas por un muelle]]” tenemos dos masas <math>m_1</math> y <math>m_2</math> se mueven a lo largo del eje OX unidas por un resorte de constante <math>k</math> y longitud natura <math>\ell_0</math>. Inicialmente las dos masas se encuentran en reposo en <math>x_{10}=0</math> y <math>x_{20}=\ell_0</math>. Entonces se le comunica a la masa <math>m_1</math> una velocidad <math>v_0</math> en el sentido positivo del eje. | Como en el problema “[[Dos masas unidas por un muelle]]” tenemos dos masas <math>m_1</math> y <math>m_2</math> se mueven a lo largo del eje OX unidas por un resorte de constante <math>k</math> y longitud natura <math>\ell_0</math>. Inicialmente las dos masas se encuentran en reposo en <math>x_{10}=0</math> y <math>x_{20}=\ell_0</math>. Entonces se le comunica a la masa <math>m_1</math> una velocidad <math>v_0</math> en el sentido positivo del eje. | ||
| Línea 7: | Línea 22: | ||
<ol start="3"> | <ol start="3"> | ||
<li>¿Cómo queda la lagrangiana en función de estas coordenadas?</li> | <li>¿Cómo queda la lagrangiana en función de estas coordenadas?</li> | ||
| - | <li>Obtenga las ecuaciones de movimiento para x_G y x.</li> | + | <li>Obtenga las ecuaciones de movimiento para <math>x_G</math> y <math>x</math>.</li> |
<li>Determine dos constantes de movimiento para este sistema.</li> | <li>Determine dos constantes de movimiento para este sistema.</li> | ||
</ol> | </ol> | ||
| + | |||
| + | ==[[Estudio analítico de una barra apoyada]]== | ||
| + | Como en el problema “[[Barra deslizante con masas en los extremos]]”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies | ||
| + | |||
| + | <center>[[Archivo:Barra-dos-masas.png|250px]]</center> | ||
| + | # Determine la lagrangiana del sistema. | ||
| + | # Halle la ecuación de movimiento para el ángulo θ. | ||
| + | # Determine una constante de movimiento no trivial. | ||
| + | # Añadiendo una coordenada x que representaría la separación de la barra respecto de la pared vertical, calcule la fuerza de reacción ejercida por la pared. | ||
| + | # Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor. | ||
| + | # Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared. | ||
==[[Péndulo compuesto. Análisis por mecánica analítica (CMR)|Péndulo compuesto]]== | ==[[Péndulo compuesto. Análisis por mecánica analítica (CMR)|Péndulo compuesto]]== | ||
| Línea 42: | Línea 68: | ||
<li>¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?</li> | <li>¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?</li> | ||
</ol> | </ol> | ||
| + | |||
| + | ==[[Dos rodillos unidos por un resorte (CMR)|Dos rodillos unidos por un resorte]]== | ||
| + | Se tiene un sistema de dos rodillos (“2” y “3”) de la misma masa m y el mismo radio R, situados sobre una superficie horizontal (sólido 1), sobre la que pueden rodar sin deslizar. Los dos rodillos no son idénticos. El “2” es un cilindro macizo homogéneo (<math>\gamma=1/2</math>), mientras que el “3” tiene su masa concentrada en la superficie cilíndrica (<math>\gamma=1</math>). Los dos rodillos están conectados por un resorte de constante k y longitud natural <math>\ell_0</math>. Todo el sistema está sometido a la acción del peso. | ||
| + | <center>[[Archivo:dos-rodillos-muelle.png|800px]]</center> | ||
| + | Estando en reposo en una posición de equilibrio, se sujeta el cilindro 2 y se desplaza el 3 una cierta distancia A, manteniéndolos en reposo. Entonces se sueltan los dos. | ||
| + | # Halle la lagrangiana de este sistema, empleando como coordenadas generalizadas las posiciones <math>x_2</math> y <math>x_3</math> de las centros de los rodillos, medidas respecto a un sistema fijo. | ||
| + | # Halle las ecuaciones de movimiento para las posiciones de los centros de los rodillos, esto es, halle <math>\ddot{x}_2</math> y <math>\ddot{x}_3</math> en función de las posiciones <math>x_2</math> y x_3. | ||
| + | Si en lugar de <math>x_2</math> y <math>x_3</math> se emplean como coordenadas <math>x_2</math> y <math>x</math>, definida x como la longitud del resorte menos su longitud en el equilibrio | ||
| + | <ol start="3"> | ||
| + | <li>¿Cómo queda la lagrangiana en función de <math>x_2</math> y <math>x</math>?</li> | ||
| + | <li>¿Y las ecuaciones de movimiento para estas coordenadas?</li> | ||
| + | <li>¿Cuál es la frecuencia de oscilación del resorte?</li> | ||
| + | <li>¿Y la posición de cada masa como función del tiempo?</li> | ||
| + | <li>¿Qué constantes de movimiento existen en este problema?</li> | ||
| + | </ol> | ||
| + | |||
| + | ==[[Estudio analítico de una partícula dentro de un tubo]]== | ||
| + | Una partícula de masa <math>m</math> se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular Ω constante alrededor del eje OZ | ||
| + | # Determine la lagrangiana de este sistema. | ||
| + | # Halle la ecuación de movimiento para la coordenada radial ρ. | ||
| + | # ¿Se conserva la energía en este sistema? Si no es así, ¿hay alguna otra magnitud similar que sí se conserve? | ||
| + | # Con ayuda de los multiplicadores de Lagrange, calcule la fuerza de reacción generalizada que el tubo ejerce sobre la partícula. | ||
| + | |||
| + | ==[[Percusión sobre una barra. Estudio analítico]]== | ||
| + | Suponga una barra homogénea, de masa <math>m</math> y longitud <math>b</math>, situada horizontalmente sobre un plano sin rozamiento. | ||
| + | |||
| + | Estando la barra en reposo, se efectúa sobre ella una percusión <math>\vec{P}_0</math> perpendicular a la dirección de la barra y a una distancia c de su centro. | ||
| + | |||
| + | Empleando las técnicas de la mecánica analítica, determine la velocidad del centro de la barra y la velocidad angular de ésta, así como las posibles fuerzas y momentos impulsivos de reacción, en los casos siguientes: | ||
| + | |||
| + | # La barra puede moverse libremente por el plano. | ||
| + | # La barra se halla articulada por un extremo A a una pared inmóvil. | ||
| + | # La barra se halla empotrada por su extremo A a una pared inmóvil. | ||
| + | |||
| + | ==[[Percusión sobre un sistema articulado]]== | ||
| + | Considerando el sistema de dos barras articuladas del problema “[[Dos barras articuladas (CMR)|dos barras articuladas]]” suponga que el sistema se halla completamente extendido y en reposo. Entonces, se efectúa una percusión <math>\vec{P}_0</math> perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras. | ||
| + | |||
| + | Determine la velocidad angular de cada barra, así como la velocidad de los puntos A y B (extremo libre de la segunda barra) en los casos: | ||
| + | |||
| + | # Se golpea la barra OA en un punto D a una distancia c de la articulación A. | ||
| + | # Se golpea la barra AB en un punto D a una distancia c de la articulación A. | ||
[[Categoría:Problemas de mecánica analítica (CMR)|0]] | [[Categoría:Problemas de mecánica analítica (CMR)|0]] | ||
última version al 21:18 12 abr 2020
1 Estudio analítico de máquina de Atwood
Una máquina de Atwood está formada por dos masas m1 y m2 unidas por un hilo ideal, inextensible y sin masa, que pasa por una polea ideal, sin rozamiento y sin masa.
- Empleando el principio de D’Alembert halle la aceleración de cada una de las masas.
- Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea.
- Suponga ahora que la polea es un disco de radio R con momento de inercia I. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda?
2 Estudio analítico del plano inclinado
Una partícula de masa m desliza sin rozamiento por un plano inclinado, de base b y altura h, sometida a la fuerza de la gravedad y las fuerzas de reacción. Empleando como coordenadas las cartesianas de la partícula con el eje OX horizontal y el OY vertical:
- Escriba la ecuación del vínculo entre las coordenadas.
- A partir del principio de D’Alembert, obtenga las componentes de la aceleración de la masa.
- Con ayuda de los multiplicadores de Lagrange, halle las componentes de la fuerza de reacción del plano sobre la masa.
3 Estudio analítico del péndulo simple
Empleando el principio de D’Alembert, obtenga las ecuaciones de movimiento para las coordenadas cartesianas de un péndulo simple que oscila verticalmente.
4 Estudio analítico de dos masas unidas por un muelle
Como en el problema “Dos masas unidas por un muelle” tenemos dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 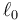 . Inicialmente las dos masas se encuentran en reposo en x10 = 0 y
. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 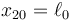 . Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
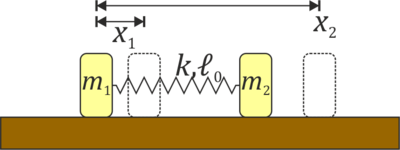
- Determine la lagrangiana del sistema en función de las posiciones de las dos partículas.
- Obtenga las ecuaciones de movimiento para x1 y x2
Realice el cambio de variables a las coordenadas generalizadas xG = (m1x1 + m2x2) / (m1 + m2),  .
.
- ¿Cómo queda la lagrangiana en función de estas coordenadas?
- Obtenga las ecuaciones de movimiento para xG y x.
- Determine dos constantes de movimiento para este sistema.
5 Estudio analítico de una barra apoyada
Como en el problema “Barra deslizante con masas en los extremos”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies
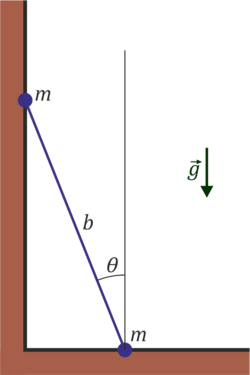
- Determine la lagrangiana del sistema.
- Halle la ecuación de movimiento para el ángulo θ.
- Determine una constante de movimiento no trivial.
- Añadiendo una coordenada x que representaría la separación de la barra respecto de la pared vertical, calcule la fuerza de reacción ejercida por la pared.
- Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor.
- Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared.
6 Péndulo compuesto
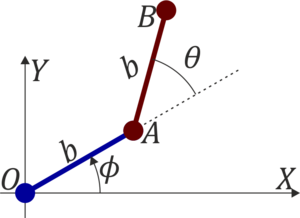
Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
Para este sistema
- Calcule la lagrangiana del sistema.
- Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
- Obtenga dos constantes de movimiento no triviales.
- Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
- Calcule el valor que debe tener la velocidad angular
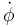 si se desea que la barra mantenga una inclinación constante respecto a la vertical.
si se desea que la barra mantenga una inclinación constante respecto a la vertical.
7 Dos barras articuladas
Un sistema está formado por dos varillas homogéneas, ambas de masa m y longitud b, situadas sobre un plano horizontal (“sólido 1”). La varilla “2” está articulada por su extremo O a un punto fijo del plano, mientras que por su extremo A está articulada a la varilla “3”.
- Escriba la lagrangiana del sistema, empleando como coordenadas generalizadas los ángulos que ambas varillas forman con el eje OX.
- Obtenga las ecuaciones de movimiento para estos dos ángulos.
- ¿Es cíclica alguna de estas coordenadas?
Si en lugar de esas coordenadas se usan el ángulo ϕ que la varilla OA forma con OX y el ángulo θ que AB forma con la prolongación de OA
- ¿Cómo queda la lagrangiana?
- ¿Y las ecuaciones de movimiento para estos ángulos?
- ¿Es cíclica alguna de estas coordenadas?
- Determine dos constantes de movimiento para este sistema.
- Con ayuda de estas constantes, reduzca el problema a una única ecuación de movimiento para el ángulo θ.
Suponga ahora que la varilla 2 es forzada a girar con velocidad angular constante Ω en torno a O.
- Escriba la lagrangiana para este sistema en función del ángulo θ.
- Obtenga la ecuación de movimiento para θ. ¿Es la misma que en el apartado (8)?
- ¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?
8 Dos rodillos unidos por un resorte
Se tiene un sistema de dos rodillos (“2” y “3”) de la misma masa m y el mismo radio R, situados sobre una superficie horizontal (sólido 1), sobre la que pueden rodar sin deslizar. Los dos rodillos no son idénticos. El “2” es un cilindro macizo homogéneo (γ = 1 / 2), mientras que el “3” tiene su masa concentrada en la superficie cilíndrica (γ = 1). Los dos rodillos están conectados por un resorte de constante k y longitud natural 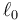 . Todo el sistema está sometido a la acción del peso.
. Todo el sistema está sometido a la acción del peso.
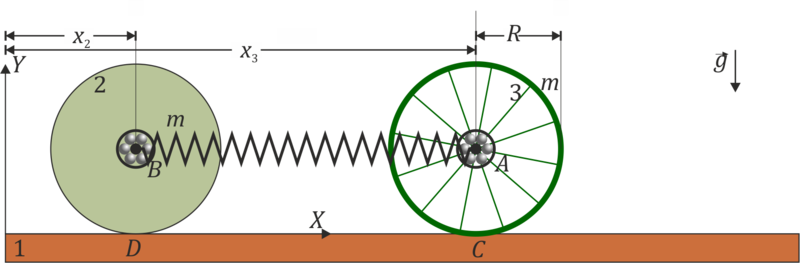
Estando en reposo en una posición de equilibrio, se sujeta el cilindro 2 y se desplaza el 3 una cierta distancia A, manteniéndolos en reposo. Entonces se sueltan los dos.
- Halle la lagrangiana de este sistema, empleando como coordenadas generalizadas las posiciones x2 y x3 de las centros de los rodillos, medidas respecto a un sistema fijo.
- Halle las ecuaciones de movimiento para las posiciones de los centros de los rodillos, esto es, halle
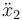 y
y 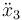 en función de las posiciones x2 y x_3.
en función de las posiciones x2 y x_3.
Si en lugar de x2 y x3 se emplean como coordenadas x2 y x, definida x como la longitud del resorte menos su longitud en el equilibrio
- ¿Cómo queda la lagrangiana en función de x2 y x?
- ¿Y las ecuaciones de movimiento para estas coordenadas?
- ¿Cuál es la frecuencia de oscilación del resorte?
- ¿Y la posición de cada masa como función del tiempo?
- ¿Qué constantes de movimiento existen en este problema?
9 Estudio analítico de una partícula dentro de un tubo
Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular Ω constante alrededor del eje OZ
- Determine la lagrangiana de este sistema.
- Halle la ecuación de movimiento para la coordenada radial ρ.
- ¿Se conserva la energía en este sistema? Si no es así, ¿hay alguna otra magnitud similar que sí se conserve?
- Con ayuda de los multiplicadores de Lagrange, calcule la fuerza de reacción generalizada que el tubo ejerce sobre la partícula.
10 Percusión sobre una barra. Estudio analítico
Suponga una barra homogénea, de masa m y longitud b, situada horizontalmente sobre un plano sin rozamiento.
Estando la barra en reposo, se efectúa sobre ella una percusión 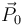 perpendicular a la dirección de la barra y a una distancia c de su centro.
perpendicular a la dirección de la barra y a una distancia c de su centro.
Empleando las técnicas de la mecánica analítica, determine la velocidad del centro de la barra y la velocidad angular de ésta, así como las posibles fuerzas y momentos impulsivos de reacción, en los casos siguientes:
- La barra puede moverse libremente por el plano.
- La barra se halla articulada por un extremo A a una pared inmóvil.
- La barra se halla empotrada por su extremo A a una pared inmóvil.
11 Percusión sobre un sistema articulado
Considerando el sistema de dos barras articuladas del problema “dos barras articuladas” suponga que el sistema se halla completamente extendido y en reposo. Entonces, se efectúa una percusión 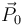 perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.
perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.
Determine la velocidad angular de cada barra, así como la velocidad de los puntos A y B (extremo libre de la segunda barra) en los casos:
- Se golpea la barra OA en un punto D a una distancia c de la articulación A.
- Se golpea la barra AB en un punto D a una distancia c de la articulación A.