Potencial de dos cargas puntuales (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== ==Solución== El potencial eléctrico en el punto P debido a una carga puntual es la cantidad escalar <center><math>V = \frac{1}{4\pi\varepsilon_0}\,\frac{q}{d}</…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | {{nivel|2}} Halle el potencial eléctrico en los puntos indicados en el problema “[[Campo de dos cargas puntuales (GIOI)|Campo de dos cargas puntuales]]”, para los pares de cargas descritos en el mismo problema. | ||
| + | |||
==Solución== | ==Solución== | ||
El potencial eléctrico en el punto P debido a una carga puntual es la cantidad escalar | El potencial eléctrico en el punto P debido a una carga puntual es la cantidad escalar | ||
última version al 21:14 14 feb 2020
1 Enunciado
![]() Halle el potencial eléctrico en los puntos indicados en el problema “Campo de dos cargas puntuales”, para los pares de cargas descritos en el mismo problema.
Halle el potencial eléctrico en los puntos indicados en el problema “Campo de dos cargas puntuales”, para los pares de cargas descritos en el mismo problema.
2 Solución
El potencial eléctrico en el punto P debido a una carga puntual es la cantidad escalar

Si tenemos más de una carga puntual, se aplica el principio de superposición
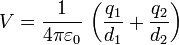
Utilizando los valores de las distancias calculadas en el primer apartado nos queda la siguiente tabla:
| q1(nC) | q2(nC) | VA(V) | VB(V) | VC(V) | VD(V) |
|---|---|---|---|---|---|
| +1 | +1 | 150 | 120 | 120 | 50.6 |
| +1 | −1 | 0 | 0 | 0 | −5.6 |
| +1 | +9 | 750 | 600 | 600 | 275.6 |
| +1 | −9 | −600 | −480 | −480 | −230.6 |
A la vista de esta tabla podemos sacar algunas conclusiones:
- Al ser el potencial escalar, los puntos B y C son equivalentes, ya que ambos se encuentran a las mismas distancias de las dos cargas.
- En el caso del dipolo (dos cargas opuestas de la misma magnitud) los puntos del plano central x = 0 (como A, B y C) se encuentran a la misma distancia de las dos cargas, por lo que los potenciales respectivos se cancelan y el resultado es un potencial nulo.





