Campo de dos cargas puntuales (GIOI)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

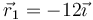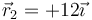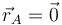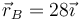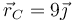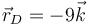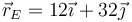
Se tienen dos cargas $q 1$ y $q 2$ situadas respectivamente en los puntos $\vec{r}_1=-12\vec{\imath}$ (cm) y $\vec{r}_2=+12\vec{\imath}$ (cm). Halle el campo eléctrico en los puntos $\vec{r}_A=\vec{0}$ , $\vec{r}_B=28\vec{\imath}$ , $\vec{r}_C=9\vec{\jmath}$ , $\vec{r}_D=-9\vec{k}$ , $\vec{r}_E=12\vec{\imath}+32\vec{\jmath}$

(todas las distancias en cm) para los cuatro casos siguientes

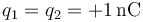
$q_1=q_2=+1\,\mathrm{nC}$
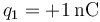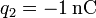
$q_1=+1\,\mathrm{nC}$ , $q_2=-1\,\mathrm{nC}$
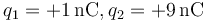
$q_1=+1\,\mathrm{nC},q_2=+9\,\mathrm{nC}$
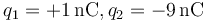
$q_1=+1\,\mathrm{nC},q_2=-9\,\mathrm{nC}$

2 Solución

2.1 Introducción

El campo eléctrico creado por una carga puntual es de la forma

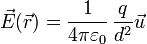
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q}{d^2}\vec{u}$

siendo $q$ la magnitud de la carga, $d$ la distancia desde el punto de observación a la posición donde se halla la carga y $\vec{u}$ el vector unitario radial en la dirección desde la posición de la carga al punto de observación y con sentido hacia afuera.

Si la carga puntual se encuentra en el punto 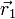$\vec{r}_1$ y el punto de observación se halla en $\vec{r}$ , se cumple que

$d = \left|\vec{r}-\vec{r}_1\right|\qquad\qquad \vec{u}=\frac{\vec{r}-\vec{r}_1}{\left|\vec{r}-\vec{r}_1\right|}$

lo que da la expresión para el campo

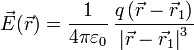
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q\left(\vec{r}-\vec{r}_1\right)}{\left|\vec{r}-\vec{r}_1\right|^3}$

Si tenemos dos cargas puntuales, el campo en cada punto será la suma de los campos individuales en dicho punto

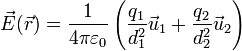
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{d_1^2}\vec{u}_1+\frac{q_2}{d_2^2}\vec{u}_2\right)$

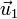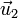siendo $d 1$ y $d 2$ las distancias desde el punto de observación a cada una de las cargas y $\vec{u}_1$ y $\vec{u}_2$ los correspondientes vectores radiales. En términos de las posiciones respectivas

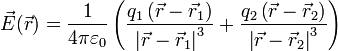
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1\left(\vec{r}-\vec{r}_1\right)}{\left|\vec{r}-\vec{r}_1\right|^3}+\frac{q_2\left(\vec{r}-\vec{r}_2\right)}{\left|\vec{r}-\vec{r}_2\right|^3}\right)$

En caso de que sea fácil medir las distancias e identificar los vectores unitarios, es preferible emplear la primera de las dos fórmulas, por su simplicidad. En caso de duda, siempre se puede recurrir a la segunda.

2.2 Punto A

En el punto intermedio entre las dos cargas, las dos distancias son iguales

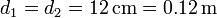
$d_1 = d_2=12\,\mathrm{cm}=0.12\,\mathrm{m}$

mientras que los vectores radiales son

$\vec{u}_1=\vec{\imath}\qquad\qquad \vec{u}_2=-\vec{\imath}$

lo que nos da los valores siguientes para el campo eléctrico

Cargas iguales: Si las dos cargas tienen la misma magnitud y el mismo signo, sus campos se cancelan y el resultado es nulo

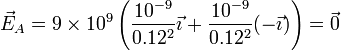
$\vec{E}_A=9\times 10^9\left(\frac{10^{-9}}{0.12^2}\vec{\imath}+\frac{10^{-9}}{0.12^2}(-\vec{\imath})\right)=\vec{0}$

Cargas opuestas: Para dos cargas de la misma magnitud y signo opuesto, el campo en el centro es el doble del que produciría cada una

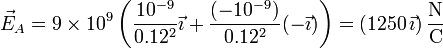
$\vec{E}_A=9\times 10^9\left(\frac{10^{-9}}{0.12^2}\vec{\imath}+\frac{(-10^{-9})}{0.12^2}(-\vec{\imath})\right)=\left(1250\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del mismo signo: Para dos cargas desiguales del mismo signo, el campo de la mayor domina sobre el de la menor

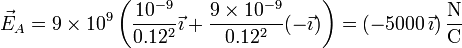
$\vec{E}_A=9\times 10^9\left(\frac{10^{-9}}{0.12^2}\vec{\imath}+\frac{9\times 10^{-9}}{0.12^2}(-\vec{\imath})\right)=\left(-5000\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del signo opuesto: Para dos cargas desiguales de signo contrario, el campo de la menor se suma al de la mayor

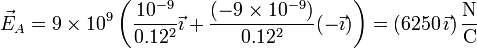
$\vec{E}_A=9\times 10^9\left(\frac{10^{-9}}{0.12^2}\vec{\imath}+\frac{(-9\times 10^{-9})}{0.12^2}(-\vec{\imath})\right)=\left(6250\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

2.3 Punto B

El punto B está sobre el eje de las dos cargas, pero a un lado de ellas. La distancia a cada carga es

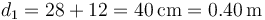
$d_1 = 28+12=40\,\mathrm{cm}=0.40\,\mathrm{m}$

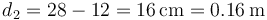
$d_2 = 28-12=16\,\mathrm{cm}=0.16\,\mathrm{m}$

mientras que los vectores radiales son iguales

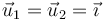
$\vec{u}_1=\vec{u}_2=\vec{\imath}$

lo que nos da los valores siguientes para el campo eléctrico

Cargas iguales

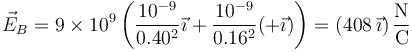
$\vec{E}_B=9\times 10^9\left(\frac{10^{-9}}{0.40^2}\vec{\imath}+\frac{10^{-9}}{0.16^2}(+\vec{\imath})\right)=\left(408\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

Cargas opuestas

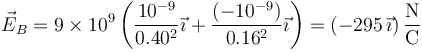
$\vec{E}_B=9\times 10^9\left(\frac{10^{-9}}{0.40^2}\vec{\imath}+\frac{(-10^{-9})}{0.16^2}\vec{\imath}\right)=\left(-295\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del mismo signo

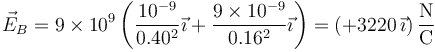
$\vec{E}_B=9\times 10^9\left(\frac{10^{-9}}{0.40^2}\vec{\imath}+\frac{9\times 10^{-9}}{0.16^2}\vec{\imath}\right)=\left(+3220\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del signo opuesto

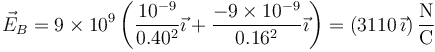
$\vec{E}_B=9\times 10^9\left(\frac{10^{-9}}{0.40^2}\vec{\imath}+\frac{-9\times 10^{-9}}{0.16^2}\vec{\imath}\right)=\left(3110\,\vec{\imath}\right)\frac{\mathrm{N}}{\mathrm{C}}$

2.4 Punto C

El punto C se encuentra situado en el plano central entre las dos cargas, pero no en la recta que pasa por ellas. La distancia a las dos cargas es la misma

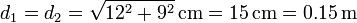
$d_1=d_2=\sqrt{12^2+9^2}\,\mathrm{cm}=15\,\mathrm{cm}=0.15\,\mathrm{m}$

mientras que los vectores unitarios correspondientes son

$\vec{u}_1 =\frac{(9\vec{\jmath})-(-12\,\vec{\imath})}{15}=\frac{4}{5}\vec{\imath}+\frac{3}{5}\vec{\jmath}=0.8\vec{\imath}+0.6\vec{\jmath}\qquad\qquad \vec{u}_2 =\frac{(9\vec{\jmath})-(12\,\vec{\imath})}{15}=-\frac{4}{5}\vec{\imath}+\frac{3}{5}\vec{\jmath}=-0.8\vec{\imath}+0.6\vec{\jmath}$

Sustituyendo obtenemos los siguientes valores para los campos.

Cargas iguales: Las componentes paralelas al eje que pasa por las cargas se anulan mutuamente y queda un campo normal a este eje.

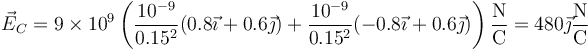
$\vec{E}_C=9\times 10^9\left(\frac{10^{-9}}{0.15^2}(0.8\vec{\imath}+0.6\vec{\jmath})+\frac{10^{-9}}{0.15^2}(-0.8\vec{\imath}+0.6\vec{\jmath})\right)\frac{\mathrm{N}}{\mathrm{C}}=480\vec{\jmath}\frac{\mathrm{N}}{\mathrm{C}}$

Cargas de la misma magnitud y signo opuesto: En este caso se anulan las componentes normales y resulta un campo paralelo a la recta que pasa por las cargas.

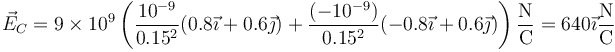
$\vec{E}_C=9\times 10^9\left(\frac{10^{-9}}{0.15^2}(0.8\vec{\imath}+0.6\vec{\jmath})+\frac{(-10^{-9})}{0.15^2}(-0.8\vec{\imath}+0.6\vec{\jmath})\right)\frac{\mathrm{N}}{\mathrm{C}}=640\vec{\imath}\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del mismo signo

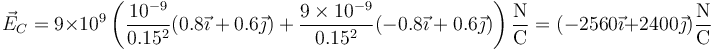
$\vec{E}_C=9\times 10^9\left(\frac{10^{-9}}{0.15^2}(0.8\vec{\imath}+0.6\vec{\jmath})+\frac{9\times 10^{-9}}{0.15^2}(-0.8\vec{\imath}+0.6\vec{\jmath})\right)\frac{\mathrm{N}}{\mathrm{C}}=(-2560\vec{\imath}+2400\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes de signo opuesto

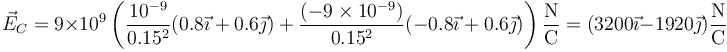
$\vec{E}_C=9\times 10^9\left(\frac{10^{-9}}{0.15^2}(0.8\vec{\imath}+0.6\vec{\jmath})+\frac{(-9\times 10^{-9})}{0.15^2}(-0.8\vec{\imath}+0.6\vec{\jmath})\right)\frac{\mathrm{N}}{\mathrm{C}}=(3200\vec{\imath}-1920\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

2.5 Punto D

El campo eléctrico de dos cargas tiene simetría de revolución. Esto quiere decir que si las cargas se encuentran sobre el eje OX, la distribución de las líneas en el plano XY es idéntico al que se obtiene en el plano XZ.

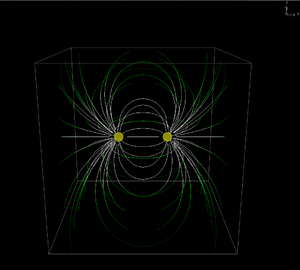
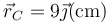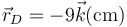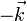Esto quiere decir que si en lugar de considerar el punto $\vec{r}_C = 9\vec{\jmath}(\mathrm{cm})$ tomamos el $\vec{r}_D = -9\vec{k}(\mathrm{cm})$ lo único que estamos cambiando es el plano XY por el XZ. Matemáticamente, esto quiere decir que resulta lo mismo que en el apartado anterior sin más que sustituir $\vec{\jmath}$ por $-\vec{k}$ . Obtenemos, por tanto:

Cargas iguales

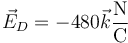
$\vec{E}_D=-480\vec{k}\frac{\mathrm{N}}{\mathrm{C}}$

Cargas de la misma magnitud y signo opuesto

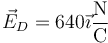
$\vec{E}_D=640\vec{\imath}\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del mismo signo

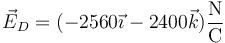
$\vec{E}_D=(-2560\vec{\imath}-2400\vec{k})\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes de signo opuesto

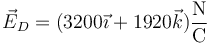
$\vec{E}_D=(3200\vec{\imath}+1920\vec{k})\frac{\mathrm{N}}{\mathrm{C}}$

2.6 Punto E

Por último, para el punto E tenemos una distancia diferente a cada carga. Midiendo todo en centímetros

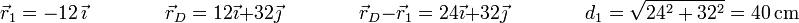
$\vec{r}_1 = -12\,\vec{\imath}\qquad\qquad \vec{r}_D=12\vec{\imath}+32\vec{\jmath}\qquad\qquad \vec{r}_D-\vec{r}_1 = 24\vec{\imath}+32\vec{\jmath}\qquad\qquad d_1 = \sqrt{24^2+32^2} = 40\,\mathrm{cm}$

y para la segunda carga

$\vec{r}_2 = 12\,\vec{\imath}\qquad\qquad \vec{r}_D=12\vec{\imath}+32\vec{\jmath}\qquad\qquad \vec{r}_E-\vec{r}_2 = 32\vec{\jmath}\qquad d_2 = 32\,\mathrm{cm}$

Los vectores unitarios radiales son en este caso

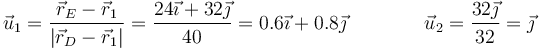
$\vec{u}_1 = \frac{\vec{r}_E-\vec{r}_1}{|\vec{r}_D-\vec{r}_1|} = \frac{24\vec{\imath}+32\vec{\jmath}}{40}=0.6\vec{\imath}+0.8\vec{\jmath}\qquad\qquad\vec{u}_2=\frac{32\vec{\jmath}}{32}=\vec{\jmath}$

Tras sustituir, obtenemos los siguientes campos

Cargas iguales

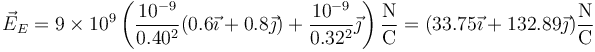
$\vec{E}_E=9\times 10^9\left(\frac{10^{-9}}{0.40^2}(0.6\vec{\imath}+0.8\vec{\jmath})+\frac{10^{-9}}{0.32^2}\vec{\jmath}\right)\frac{\mathrm{N}}{\mathrm{C}}=(33.75\vec{\imath}+132.89\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

Cargas de la misma magnitud y signo opuesto: En este caso se anulan las componentes normales y resulta un campo paralelo a la recta que pasa por las cargas.

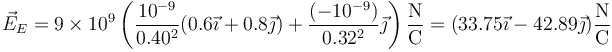
$\vec{E}_E=9\times 10^9\left(\frac{10^{-9}}{0.40^2}(0.6\vec{\imath}+0.8\vec{\jmath})+\frac{(-10^{-9})}{0.32^2}\vec{\jmath}\right)\frac{\mathrm{N}}{\mathrm{C}}=(33.75\vec{\imath}-42.89\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes del mismo signo

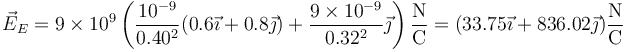
$\vec{E}_E=9\times 10^9\left(\frac{10^{-9}}{0.40^2}(0.6\vec{\imath}+0.8\vec{\jmath})+\frac{9\times 10^{-9}}{0.32^2}\vec{\jmath}\right)\frac{\mathrm{N}}{\mathrm{C}}=(33.75\vec{\imath}+836.02\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

Cargas diferentes de signo opuesto

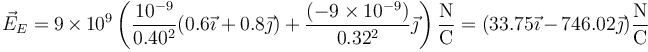
$\vec{E}_E=9\times 10^9\left(\frac{10^{-9}}{0.40^2}(0.6\vec{\imath}+0.8\vec{\jmath})+\frac{(-9\times 10^{-9})}{0.32^2}\vec{\jmath}\right)\frac{\mathrm{N}}{\mathrm{C}}=(33.75\vec{\imath}-746.02\vec{\jmath})\frac{\mathrm{N}}{\mathrm{C}}$

Obsérvese como en todos los casos la componente X es la misma, por ser el campo de la segunda carga puramente en la dirección Y.

2.7 Resumen

Podemos tabular todos los resultados en una tabla-resumen

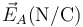
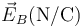
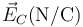
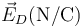
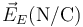
$q 1 (nC)$	$q 2 (nC)$	$\vec{E}_A (\mathrm{N}/\mathrm{C})$	$\vec{E}_B (\mathrm{N}/\mathrm{C})$	$\vec{E}_C (\mathrm{N}/\mathrm{C})$	$\vec{E}_D (\mathrm{N}/\mathrm{C})$	$\vec{E}_E (\mathrm{N}/\mathrm{C})$
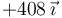
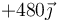
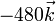
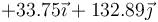
+1	+1	$\vec{0}$	$+408\,\vec{\imath}$	$+480\vec{\jmath}$	$-480\vec{k}$	$+33.75\vec{\imath}+132.89\vec{\jmath}$
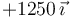
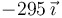
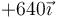
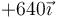
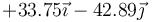
+1	−1	$+1250\,\vec{\imath}$	$-295\,\vec{\imath}$	$+640\vec{\imath}$	$+640\vec{\imath}$	$+33.75\vec{\imath}-42.89\vec{\jmath}$
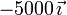
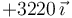
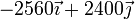
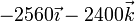
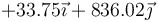
+1	+9	$-5000\,\vec{\imath}$	$+3220\,\vec{\imath}$	$-2560\vec{\imath}+2400\vec{\jmath}$	$-2560\vec{\imath}-2400\vec{k}$	$+33.75\vec{\imath}+836.02\vec{\jmath}$
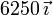
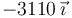
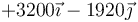
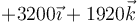
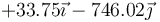
+1	−9	$6250\,\vec{\imath}$	$-3110\,\vec{\imath}$	$+3200\vec{\imath}-1920\vec{\jmath}$	$+3200\vec{\imath}+1920\vec{k}$	$+33.75\vec{\imath}-746.02\vec{\jmath}$