Coordenadas esféricas. Líneas y superficies coordenadas
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Líneas coordenadas== ==Superficies coordenadas== ==Artículo siguiente== Resumen de líneas y superficies coordenadas ==Artículo anterior== [[Coordenadas cilíndricas. Lín...) |
(→Enlaces) |
||
| (14 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Líneas coordenadas== | ==Líneas coordenadas== | ||
| + | [[Imagen:esf-lin.png|300px|left]][[Imagen:Latitud.png|200px|right]] | ||
| + | * Para la coordenada <math>\varphi</math> obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los ''paralelos''. | ||
| + | |||
| + | * Al variar <math>\theta\,</math> modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los ''meridianos''). Son semicircunferencias y no circunferencias completas porque la colatitud solo llega hasta <math>\pi\,</math>. | ||
| + | |||
| + | * Al alejarnos o acercarnos al origen de coordenadas, variando <math>r\,</math>, nos movemos sobre una semirrecta (''no'' una recta) que, partiendo del origen de coordenadas, pasa por el punto <math>P\,</math>. | ||
==Superficies coordenadas== | ==Superficies coordenadas== | ||
| + | [[Imagen:esf-sup.png|right]] | ||
| + | * La superficie <math>r = \mathrm{cte}\,</math> la forman los puntos situados a la misma distancia del origen de coordenadas. Esto, por definición, es una superficie esférica, de la cual toman nombre las coordenadas. | ||
| - | = | + | * La superficie <math>\varphi = \mathrm{cte}</math> es, como en [[Coordenadas cilíndricas. Líneas y superficies coordenadas| cilíndricas]], un semiplano con borde el eje <math>Z\,</math>. |
| - | [[ | + | |
| - | = | + | * Para construir la superficie <math>\theta = \mathrm{cte}\,</math> podemos partir de las líneas coordenadas <math>r\,</math>, que son semirrectas que parten del origen de coordenadas y forman un ángulo fijo con el eje <math>Z\,</math>. Si ahora permitimos que varíe <math>\varphi</math> lo que hacemos es girar estas semirrectas en torno al eje <math>Z\,</math> manteniendo constante el ángulo con este eje. El resultado es una superficie cónica de semiángulo en el vértice <math>\theta\,</math>. |
| - | + | ||
| - | == | + | ==Enlaces== |
| - | [[Coordenadas esféricas. Definición]] | + | * '''Siguiente:''' [[Elección de ejes y simetría]] |
| + | * '''Anterior''' [[Coordenadas cilíndricas. Líneas y superficies coordenadas]] | ||
| + | * [[Coordenadas esféricas. Definición]] | ||
| + | * [[Coordenadas esféricas. Base vectorial]] | ||
| - | [[Categoría: | + | [[Categoría:Líneas coordenadas|40]] |
| + | [[Categoría:Coordenadas esféricas|20]] | ||
última version al 11:22 23 nov 2007
1 Líneas coordenadas
- Para la coordenada
obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los paralelos.
- Al variar
modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los meridianos). Son semicircunferencias y no circunferencias completas porque la colatitud solo llega hasta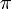 
.
- Al alejarnos o acercarnos al origen de coordenadas, variando
, nos movemos sobre una semirrecta (no una recta) que, partiendo del origen de coordenadas, pasa por el punto 
.
2 Superficies coordenadas
- La superficie
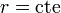la forman los puntos situados a la misma distancia del origen de coordenadas. Esto, por definición, es una superficie esférica, de la cual toman nombre las coordenadas.
- La superficie
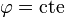es, como en cilíndricas, un semiplano con borde el eje 
.
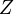- Para construir la superficie
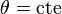podemos partir de las líneas coordenadas , que son semirrectas que parten del origen de coordenadas y forman un ángulo fijo con el eje 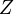. Si ahora permitimos que varíe lo que hacemos es girar estas semirrectas en torno al eje 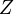manteniendo constante el ángulo con este eje. El resultado es una superficie cónica de semiángulo en el vértice .
