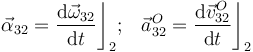Primera Convocatoria Ordinaria 2017/18 (F1 G.I.A.)

De Laplace

Revisión de 12:04 20 ago 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Partícula en movimiento con trayectoria y ley horaria conocidas) ← Edición más antigua		última version al 12:06 29 ago 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales)
(5 ediciones intermedias no se muestran.)
Línea 14:		Línea 14:
	==[[Fuerzas de interacción y aceleraciones en sistema de tres partículas, F1 GIA (Ene, 2018)|Interacciones y aceleraciones en sistema de tres partículas]]==		==[[Fuerzas de interacción y aceleraciones en sistema de tres partículas, F1 GIA (Ene, 2018)|Interacciones y aceleraciones en sistema de tres partículas]]==
	[[Archivo:f1_gIA_ex1ac_17_18_e2_0.png|right]]Tres partículas <math>P_O</math>, <math>P_1</math> y <math>P_2</math>, de masas conocidas con valores <math>m_0</math>, <math>m_1</math> y <math>m_2</math>, respectivamente, interaccionan entre sí de manera que la fuerza <math>\vec{F}_{ij}</math> que la partícula <math>P_j</math> ejerce sobre la <math>P_i</math>, tiene la dirección del segmento <math>\overrightarrow{P_jP_i}</math> (es decir, <math>\vec{F}_{ij}\parallel\pm\overrightarrow{P_jP_i}</math>). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano <math>OXYZ</math> tal que dicho triángulo está contenido en plano <math>OXY</math>, con el segmento <math>\overrightarrow{P_2P_1}</math> paralelo al eje <math>OX</math>, y la partícula <math>P_0</math> en el punto <math>O</math>. En dicho instante, las aceleraciones de las partículas <math>P_1</math> y <math>P_2</math> tiene igual dirección y sentido, siendo paralelas y opuestas al eje <math>OY</math>; es decir <math>\vec{a}_1=-a_1\!\ \vec{\jmath}\ </math> y <math>\ \vec{a}_2=-a_2\!\ \vec{\jmath}</math>, respectivamente, con <math>a_1\mathrm{,}\, a_2>0</math>		[[Archivo:f1_gIA_ex1ac_17_18_e2_0.png|right]]Tres partículas <math>P_O</math>, <math>P_1</math> y <math>P_2</math>, de masas conocidas con valores <math>m_0</math>, <math>m_1</math> y <math>m_2</math>, respectivamente, interaccionan entre sí de manera que la fuerza <math>\vec{F}_{ij}</math> que la partícula <math>P_j</math> ejerce sobre la <math>P_i</math>, tiene la dirección del segmento <math>\overrightarrow{P_jP_i}</math> (es decir, <math>\vec{F}_{ij}\parallel\pm\overrightarrow{P_jP_i}</math>). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano <math>OXYZ</math> tal que dicho triángulo está contenido en plano <math>OXY</math>, con el segmento <math>\overrightarrow{P_2P_1}</math> paralelo al eje <math>OX</math>, y la partícula <math>P_0</math> en el punto <math>O</math>. En dicho instante, las aceleraciones de las partículas <math>P_1</math> y <math>P_2</math> tiene igual dirección y sentido, siendo paralelas y opuestas al eje <math>OY</math>; es decir <math>\vec{a}_1=-a_1\!\ \vec{\jmath}\ </math> y <math>\ \vec{a}_2=-a_2\!\ \vec{\jmath}</math>, respectivamente, con <math>a_1\mathrm{,}\, a_2>0</math>
		+
		+	# Determine qué relación verifican los módulos de dichas aceleraciones, <math>|\vec{a}_1|/|\vec{a}_2|</math>, en función de las masas de las partículas.
		+	# Determine la dirección y el sentido de la aceleración <math>\vec{a}_0</math> de la partícula <math>P_0</math>. ¿Cuánto vale su módulo en relación con los módulos de las aceleraciones de <math>P_1</math> y <math>P_2</math>?
		+
		+
		+	==[[Sonda espacial sometida a la atracción gravitatoria de un planeta, F1 GIA (Ene, 2018)|Sonda espacial sometida a la atracción gravitatoria de un planeta]]==
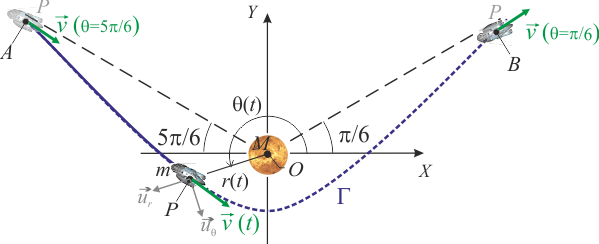
		+	Una sonda espacial, que se considera como partícula material <math>P</math> de masa <math>m</math> se dirige a un planeta de masa <math>M</math>, sometida exclusivamente a la acción gravitatoria de éste. El planeta está situado en el origen <math>O</math> de un sistema de referencia inercial <math>OXYZ</math> tal que la trayectoria <math>\Gamma</math> seguida por la sonda está contenida en el plano <math>OXY</math>. Si se utilizan las coordenadas polares para indicar la posición de la sonda/partícula en cada instante, la trayectoria <math>\Gamma</math> seguida por la partícula en su movimiento de aproximación al planeta y su posterior alejamiento,queda descrita por la siguiente ecuación:
		+
		+	<center><math>\overrightarrow{OP}= \vec{r}(t)=r(t)\!\ \left[\cos \theta (t)\!\ \vec{\imath}+ \mathrm{sen}\!\ \theta(t)\!\ \vec{\jmath}\right]=r(t)\!\ \vec{u}_r (t)\quad \Longrightarrow\quad \Gamma: r(\theta)=\frac{2\!\ b}{1- 2\!\  \mathrm{sen}\!\ \theta}\mathrm{,}\quad \mathrm{con}\;\; \frac{5\pi}{6}<\theta< 2\pi+\frac{\pi}{6}</math></center>
		+
		+	Cuando se encuentra a distancias muy grandes del planeta (<math>r\longrightarrow\infty</math>), la sonda sigue trayectorias prácticamente rectilíneas y paralelas a las rectas <math>\theta=5\pi/6</math>, cuando se aproxima al planeta), y <math>\theta=\pi/6</math> cuando se aleja. En consecuencia, cuando la sonda se aproxima al planeta, pero aún se encuentra a una gran distancia de éste, la velocidad instantánea de aquélla, <math>\, \vec{v}(\theta\approx5\pi/6)</math>, tiene la dirección y sentido del vector <math>\vec{u} =(1/2)\!\ \big[\sqrt{3}\!\ \vec{\imath}-\vec{\jmath}\big]</math> (es decir, paralela a la recta correspondiente a <math>\theta=5\!\ \pi/6</math>); además, su módulo es <math>\, v_0=\sqrt{3GM/2b}</math>.
		+
		+	Por otra parte, la sonda alcanza su máxima aproximación al planeta en el instante <math>t_m</math>, cuando se encuentra en la posición <math>\theta(t_m)=3\pi/2</math>, donde se verifica que la velocidad de la sonda es perpendicular al radio-vector posición.
		+
		+	[[Archivo:f1_gIA_ex1ac_17_18_e3_0.png|right]]
		+	# Obtenga una expresión para el módulo de la velocidad (celeridad) de la sonda, como una función de su posición, dada por el valor del ángulo <math>\theta</math>,  <math>|\vec{v}|=v(\theta)</math>.
		+	# Determine la dirección, el sentido y el módulo del momento cinético de la partícula respecto de <math>O</math> (magnitud vectorial <math>\vec{L}_O</math>) en un instante <math>t</math> cualquiera, en el cuál la sonda ocupa la posición dada por <math>\theta (t)</math>.
		+
		+	&nbsp;
		+
		+	==[[Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales, F1 GIA (Ene, 2018)|Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales]]==
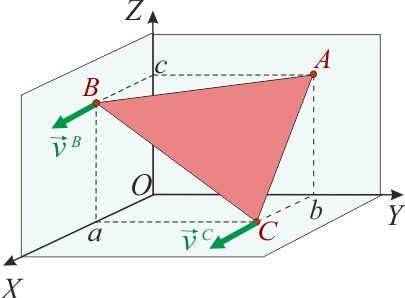
		+	[[Archivo:f1_gIA_ex1ac_17_18_e4_0.png|right]]Un sólido rígido con forma de triángulo plano se mueve con sus vértices <math>A</math>, <math>B</math> y <math>C</math> en contacto permanente con los respectivos planos <math>OYZ</math>, <math>OXZ</math> y <math>OXY</math>, de manera que en todo momento se verificará
		+
		+	<center><math>\vec{v}^A\perp\vec{\imath}\mathrm{;}\quad \vec{v}^B\perp\vec{\jmath}\mathrm{;}\quad \vec{v}^C\perp\vec{k}</math></center>
		+
		+	En un determinado instante en que los vértices del triángulo ocupan los puntos de coordenadas conocidas <math>A(0,b,c)\mathrm{,}\;\; B(a,0,c)\mathrm{,}\,</math> y <math>\, C(a,b,0)</math>, se comprueba que las velocidades de <math>B</math> y <math>C</math> son idénticas (<math>\vec{v}^B=\vec{v}^C</math>), siendo <math>v_0</math> el módulo de ambas.
		+
		+	# Determine las componentes de la velocidad del vértice <math>A</math> en dicho instante.
		+	# También en el instante considerado, ¿qué dirección debe tener el vector rotación <math>\vec{\omega}</math>, característico del movimiento del sólido? Justifique su respuesta y obtenga la expresión analítica (componentes) de dicho vector.
		+
		+
		+	==[[Movimiento plano de semidisco y barra sobre plano fijo, F1 GIA (Ene, 2018)|Movimiento plano de semidisco y barra sobre plano fijo]]==
		+	[[Archivo:f1_gIA_ex1ac_17_18_e5_0_0.png|right]] El semidisco de radio <math>R</math> y &ldquo;centro&rdquo; <math>C</math> (sólido &ldquo;2&rdquo;), y la barra <math>OA</math>  de longitud <math>|\overrightarrow{OA}|=\sqrt{2}\!\  R</math> (sólido &ldquo;0&rdquo;) que se muestran en la figura, se mueven contenidos en todo momento en el plano fijo <math>\Pi_1\equiv O_1X_1Y_1</math>$ (sólido &ldquo;1&rdquo;). El extremo <math>A</math> de la barra se halla articulado en el extremo del diámetro <math>ACD</math> del semidisco, de manera que el punto del sólido &ldquo;2&rdquo; que ocupa la posición <math>A</math> se encuentra en reposo permanente respecto del sólido &ldquo;0&rdquo; (es decir, <math>\vec{v}_{20}^A=\vec{0}</math> en todo instante). El extremo <math>O</math> de la barra &ldquo;0&rdquo; desliza sobre la superficie horizontal que se corresponde con el eje <math>O_1X_1</math>. Por su parte, el semidisco <math>2</math> mantiene un contacto puntual con la superficie horizontal que constituye el sólido &ldquo;1&rdquo; y que coincide con el eje <math>O_1X_1</math>, por lo que su &ldquo;centro&rdquo; <math>C</math> se mantiene siempre a una distancia <math>R</math> de dicho eje, desplazándose con velocidad siempre paralela al mismo. En el instante considerado, el diámetro <math>ACD</math> esta colocado paralelo al eje <math>O_1X_1</math>; el punto <math>C</math> se desplaza con velocidad <math>v_0</math> en el sentido negativo del eje <math>O_1X_1</math>, a la vez que rueda sin deslizar en el punto correspondiente a la posición de contacto <math>B</math> (es decir, <math>\vec{v}_{21}^B=\vec{0}</math>). Para dicho instante...
		+
		+	# Indique las posiciones correspondientes a los C.I.R. de los movimientos {21}, {20} y {01}. Justifique su respuesta.
		+	# Obtenga los vectores rotación instantánea <math>\vec{\omega}_{21}\mathrm{;}\;\vec{\omega}_{01}\mathrm{;}\,</math> y <math>\, \vec{\omega}_{20}</math>, y la velocidad con que desliza el extremo <math>O</math> de la barra &ldquo;0&rdquo;
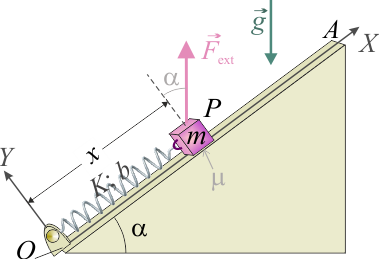
	==[[Cuerpo puntual sobre rampa con rozamiento y resorte, F1 GIA (Ene, 2018)|Cuerpo puntual sobre rampa con rozamiento y resorte]]==		==[[Cuerpo puntual sobre rampa con rozamiento y resorte, F1 GIA (Ene, 2018)|Cuerpo puntual sobre rampa con rozamiento y resorte]]==
Línea 24:		Línea 60:
	# Estando la partícula en el punto <math>O</math>, se aplica una fuerza <math>\vec{F}_\mathrm{ext}</math>, que en todo momento tiene la dirección y sentido opuesto al peso de la partícula para que ésta ascienda por la rampa; es decir, <math>\vec{F}_\mathrm{ext}=F(x)\!\ [(3/5)\!\ \vec{\imath}+(4/5)\!\ \vec{\jmath}]</math>. ¿Cómo deber ser <math>F(x)</math> para que la partícula se desplace a lo largo de la rampa con velocidad constante? ¿Cuál debe ser su valor máximo para que la partícula no pierda el contacto con la rampa?		# Estando la partícula en el punto <math>O</math>, se aplica una fuerza <math>\vec{F}_\mathrm{ext}</math>, que en todo momento tiene la dirección y sentido opuesto al peso de la partícula para que ésta ascienda por la rampa; es decir, <math>\vec{F}_\mathrm{ext}=F(x)\!\ [(3/5)\!\ \vec{\imath}+(4/5)\!\ \vec{\jmath}]</math>. ¿Cómo deber ser <math>F(x)</math> para que la partícula se desplace a lo largo de la rampa con velocidad constante? ¿Cuál debe ser su valor máximo para que la partícula no pierda el contacto con la rampa?
	# Calcule el trabajo realizado por la fuerza <math>\vec{F}_\mathrm{ext}</math> para llevar la partícula desde <math>O</math> hasta el punto <math>P_0=P(x_0,0)</math> en que pierde el contacto con la rampa. ¿Y qué trabajo ha realizado la fuerza de rozamiento en el proceso?		# Calcule el trabajo realizado por la fuerza <math>\vec{F}_\mathrm{ext}</math> para llevar la partícula desde <math>O</math> hasta el punto <math>P_0=P(x_0,0)</math> en que pierde el contacto con la rampa. ¿Y qué trabajo ha realizado la fuerza de rozamiento en el proceso?
		+
		+
		+	==[[Dos discos en planos ortogonales rodando sin deslizar sobre un plano fijo, F1 GIA (Ene, 2018)|Dos discos en planos ortogonales rodando sin deslizar sobre un plano fijo]]==
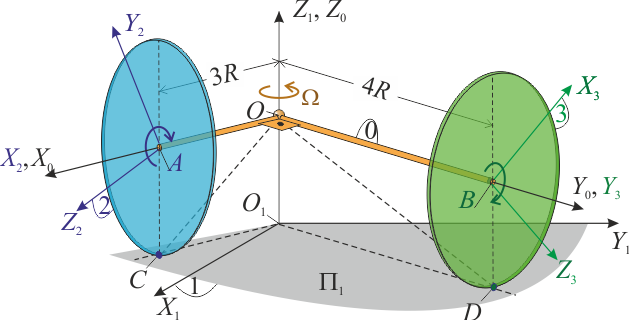
		+	En el sistema de la figura, el sólido &ldquo;0&rdquo; consiste en dos barras <math>OA</math> y <math>OB</math> de direcciones perpendiculares y rígidamente unidas entre sí, que determinan los respectivos ejes <math>OX_0</math> y <math>OY_0</math> del sistema de referencia ligado a dicho sólido. Las longitudes de los brazos son tales que <math>\overrightarrow{OA}=3\!\ R\!\ \vec{\imath}_0</math>, y <math>\overrightarrow{OB}=4\!\  R\!\ \vec{\jmath}_0</math>. Este sólido &ldquo;0&rdquo; se mueve respecto de un sistema de referencia <math>O_1X_1Y_1Z_1</math>
		+	(sólido &ldquo;1&rdquo;) de manera que, en todo momento, <math>OZ_0\|O_1Z_1</math> y la posición del punto <math>O</math> es, <math>\overrightarrow{O_1O}=R\!\ \vec{k}_1</math>. Así, la reducción cinemática de dicho movimiento en todo instante de tiempo es:
		+	[[Archivo:f1_gIA_ex1ac_17_18_p2_0.png|right]]
		+	<center><math>S_{01}\equiv\bigg\{\vec{\omega}_{01}=\Omega\!\ \vec{k}_{1,0}\mathrm{;}\quad \vec{v}_{01}^O=\vec{0}\bigg\}\mathrm{,}\;\;\forall\, t</math></center>
		+
		+	siendo <math>\Omega</math> un valor constante. Un disco de radio <math>R</math> (sólido &ldquo;2&rdquo;), con su centro fijado en el extremo <math>A</math> del sólido &ldquo;0&rdquo;, se mantiene siempre en el plano perpendicular al brazo <math>OA</math>, girando en torno a éste. Un segundo disco de igual radio <math>R</math> (sólido &ldquo;3&rdquo;), con su centro fijado en el extremo <math>B</math> del brazo <math>OB</math>, se mantiene siempre en el plano perpendicular a dicho brazo, girando en torno al mismo. Además, los discos &ldquo;2&rdquo; y &ldquo;3&rdquo; ruedan y/o pivotan sin deslizar sobre el plano fijo <math>\, \Pi_1=O_1X_1Y_1\, </math> del sólido &ldquo;1&rdquo;, en los respectivos puntos de contacto <math>C</math> y <math>D</math>.
		+
		+	# Obtenga las reducciones cinemáticas correspondientes a los movimientos de los discos respecto del plano fijo <math>\Pi_1</math> (movimientos {21} y {31}). Se sugiere utilizar la posición <math>O</math> como centro de reducción, y el sistema de referencia asociado al sólido &ldquo;0&rdquo; para describir los vectores.
		+	# Obtenga la reducción cinemática del movimiento del disco &ldquo;3&rdquo; respecto del disco &ldquo;2&rdquo; (movimiento {32}). Discuta qué tipo de movimiento es y la posición de los puntos con velocidad mínima en dicho movimiento.
		+	# Obtenga las derivadas temporales de los vectores de la reducción cinemática del movimiento {32}, <math>\displaystyle
		+	\vec{\alpha}_{32}=\frac{\mathrm{d}\vec{\omega}_{32}}{\mathrm{d}t}\bigg\rfloor_{2}\mathrm{;}\quad
		+	\vec{a}_{32}^O=\frac{\mathrm{d}\vec{v}_{32}^O}{\mathrm{d}t}\bigg\rfloor_{2}</math>
	[[Categoría:Problemas de examen F1 GIA]]		[[Categoría:Problemas de examen F1 GIA]]

---

última version al 12:06 29 ago 2018

Contenido 1 Partícula en movimiento con trayectoria y ley horaria conocidas 2 Interacciones y aceleraciones en sistema de tres partículas 3 Sonda espacial sometida a la atracción gravitatoria de un planeta 4 Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales 5 Movimiento plano de semidisco y barra sobre plano fijo 6 Cuerpo puntual sobre rampa con rozamiento y resorte 7 Dos discos en planos ortogonales rodando sin deslizar sobre un plano fijo

1 Partícula en movimiento con trayectoria y ley horaria conocidas

Una partícula P se mueve respecto de un sistema de referencia cartesiano OXYZ, recorriendo la curva Γ descrita por la ecuación paramétrica:

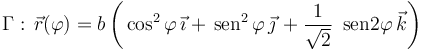
El movimiento de la partícula tiene lugar en el intervalo 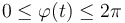, según la ley horaria 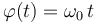. Los parámetros b y ω₀ tienen valores constantes conocidos.

Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria 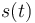para el parámetro arco.

2 Interacciones y aceleraciones en sistema de tres partículas

Tres partículas P_O, P₁ y P₂, de masas conocidas con valores m₀, m₁ y m₂, respectivamente, interaccionan entre sí de manera que la fuerza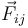 que la partícula P_j ejerce sobre la P_i, tiene la dirección del segmento 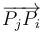(es decir, 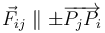). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano OXYZ tal que dicho triángulo está contenido en plano OXY, con el segmento 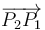paralelo al eje OX, y la partícula P₀ en el punto O. En dicho instante, las aceleraciones de las partículas P₁ y P₂ tiene igual dirección y sentido, siendo paralelas y opuestas al eje OY; es decir 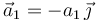y 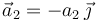, respectivamente, con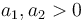

1. Determine qué relación verifican los módulos de dichas aceleraciones, 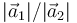, en función de las masas de las partículas.
2. Determine la dirección y el sentido de la aceleración 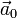de la partícula P₀. ¿Cuánto vale su módulo en relación con los módulos de las aceleraciones de P₁ y P₂?

3 Sonda espacial sometida a la atracción gravitatoria de un planeta

Una sonda espacial, que se considera como partícula material P de masa m se dirige a un planeta de masa M, sometida exclusivamente a la acción gravitatoria de éste. El planeta está situado en el origen O de un sistema de referencia inercial OXYZ tal que la trayectoria Γ seguida por la sonda está contenida en el plano OXY. Si se utilizan las coordenadas polares para indicar la posición de la sonda/partícula en cada instante, la trayectoria Γ seguida por la partícula en su movimiento de aproximación al planeta y su posterior alejamiento,queda descrita por la siguiente ecuación:

Cuando se encuentra a distancias muy grandes del planeta (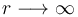), la sonda sigue trayectorias prácticamente rectilíneas y paralelas a las rectas θ = 5π / 6, cuando se aproxima al planeta), y θ = π / 6 cuando se aleja. En consecuencia, cuando la sonda se aproxima al planeta, pero aún se encuentra a una gran distancia de éste, la velocidad instantánea de aquélla, 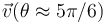, tiene la dirección y sentido del vector (es decir, paralela a la recta correspondiente a 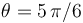); además, su módulo es .

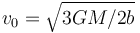Por otra parte, la sonda alcanza su máxima aproximación al planeta en el instante t_m, cuando se encuentra en la posición θ(t_m) = 3π / 2, donde se verifica que la velocidad de la sonda es perpendicular al radio-vector posición.

1. Obtenga una expresión para el módulo de la velocidad (celeridad) de la sonda, como una función de su posición, dada por el valor del ángulo θ, .
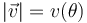2. Determine la dirección, el sentido y el módulo del momento cinético de la partícula respecto de O (magnitud vectorial ) en un instante t cualquiera, en el cuál la sonda ocupa la posición dada por θ(t).

 

4 Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales

Un sólido rígido con forma de triángulo plano se mueve con sus vértices A, B y C en contacto permanente con los respectivos planos OYZ, OXZ y OXY, de manera que en todo momento se verificará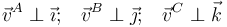

En un determinado instante en que los vértices del triángulo ocupan los puntos de coordenadas conocidas 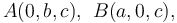y 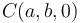, se comprueba que las velocidades de B y C son idénticas (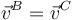), siendo v₀ el módulo de ambas.

1. Determine las componentes de la velocidad del vértice A en dicho instante.
2. También en el instante considerado, ¿qué dirección debe tener el vector rotación , característico del movimiento del sólido? Justifique su respuesta y obtenga la expresión analítica (componentes) de dicho vector.

5 Movimiento plano de semidisco y barra sobre plano fijo

El semidisco de radio R y “centro” C (sólido “2”), y la barra OA de longitud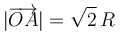 (sólido “0”) que se muestran en la figura, se mueven contenidos en todo momento en el plano fijo 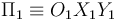$ (sólido “1”). El extremo A de la barra se halla articulado en el extremo del diámetro ACD del semidisco, de manera que el punto del sólido “2” que ocupa la posición A se encuentra en reposo permanente respecto del sólido “0” (es decir, 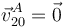en todo instante). El extremo O de la barra “0” desliza sobre la superficie horizontal que se corresponde con el eje O₁X₁. Por su parte, el semidisco 2 mantiene un contacto puntual con la superficie horizontal que constituye el sólido “1” y que coincide con el eje O₁X₁, por lo que su “centro” C se mantiene siempre a una distancia R de dicho eje, desplazándose con velocidad siempre paralela al mismo. En el instante considerado, el diámetro ACD esta colocado paralelo al eje O₁X₁; el punto C se desplaza con velocidad v₀ en el sentido negativo del eje O₁X₁, a la vez que rueda sin deslizar en el punto correspondiente a la posición de contacto B (es decir, 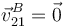). Para dicho instante...

1. Indique las posiciones correspondientes a los C.I.R. de los movimientos {21}, {20} y {01}. Justifique su respuesta.
2. Obtenga los vectores rotación instantánea 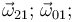y 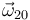, y la velocidad con que desliza el extremo O de la barra “0”

6 Cuerpo puntual sobre rampa con rozamiento y resorte

Un cuerpo que puede ser considerado como un punto material P de masa m, se encuentra en una rampa estrecha OA que forma con la horizontal un ángulo α tal que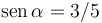 y 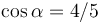. Entre partícula y rampa se establece un contacto unilateral; además, el contacto es rugoso, estando caracterizado por un coeficiente de rozamiento seco, que aproximadamente tiene el mismo valor, tanto para el caso estático como para el dinámico

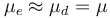. Un resorte de longitud natural b y constante recuperadora K conecta la partícula P con el extremo fijo de la rampa, O. Se sugiere utilizar un sistema de referencia cartesiano en que la rampa coincide con el eje OX y el eje OY es perpendicular a la superficie Σ de la misma. Los parámetros del sistema presentan valores tales que verifican la relación .

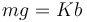1. Obtenga la posición de la rampa en que la partícula se mantendría en equilibrio, P_eq = P(x_eq,0), en el caso en que no hubiese rozamiento (μ = 0). Calcule el valor de la reacción normal del plano-rampa sobre la partícula.
2. Analice el equilibrio del sistema en el caso de que exista rozamiento (), y obtenga la expresión algebraica que permite determinar el rango de posiciones de equilibrio de la partícula en la rampa. ¿Cuál es dicho rango para el caso μ = 1 / 2?
3. Estando la partícula en el punto O, se aplica una fuerza , que en todo momento tiene la dirección y sentido opuesto al peso de la partícula para que ésta ascienda por la rampa; es decir, . ¿Cómo deber ser F(x) para que la partícula se desplace a lo largo de la rampa con velocidad constante? ¿Cuál debe ser su valor máximo para que la partícula no pierda el contacto con la rampa?
4. Calcule el trabajo realizado por la fuerza para llevar la partícula desde O hasta el punto P₀ = P(x₀,0) en que pierde el contacto con la rampa. ¿Y qué trabajo ha realizado la fuerza de rozamiento en el proceso?

7 Dos discos en planos ortogonales rodando sin deslizar sobre un plano fijo

En el sistema de la figura, el sólido “0” consiste en dos barras OA y OB de direcciones perpendiculares y rígidamente unidas entre sí, que determinan los respectivos ejes OX₀ y OY₀ del sistema de referencia ligado a dicho sólido. Las longitudes de los brazos son tales que 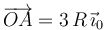, y 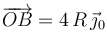. Este sólido “0” se mueve respecto de un sistema de referencia O₁X₁Y₁Z₁ (sólido “1”) de manera que, en todo momento, 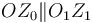y la posición del punto O es, 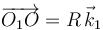. Así, la reducción cinemática de dicho movimiento en todo instante de tiempo es:

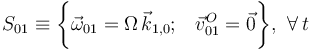
siendo Ω un valor constante. Un disco de radio R (sólido “2”), con su centro fijado en el extremo A del sólido “0”, se mantiene siempre en el plano perpendicular al brazo OA, girando en torno a éste. Un segundo disco de igual radio R (sólido “3”), con su centro fijado en el extremo B del brazo OB, se mantiene siempre en el plano perpendicular a dicho brazo, girando en torno al mismo. Además, los discos “2” y “3” ruedan y/o pivotan sin deslizar sobre el plano fijo 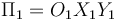del sólido “1”, en los respectivos puntos de contacto C y D.

1. Obtenga las reducciones cinemáticas correspondientes a los movimientos de los discos respecto del plano fijo Π₁ (movimientos {21} y {31}). Se sugiere utilizar la posición O como centro de reducción, y el sistema de referencia asociado al sólido “0” para describir los vectores.
2. Obtenga la reducción cinemática del movimiento del disco “3” respecto del disco “2” (movimiento {32}). Discuta qué tipo de movimiento es y la posición de los puntos con velocidad mínima en dicho movimiento.
3. Obtenga las derivadas temporales de los vectores de la reducción cinemática del movimiento {32},