Movimiento plano de semidisco y barra sobre plano fijo, F1 GIA (Ene, 2018)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Posiciones de los C.I.R. de los movimientos relativos
- 2.2 Vectores rotación instantánea

1 Enunciado

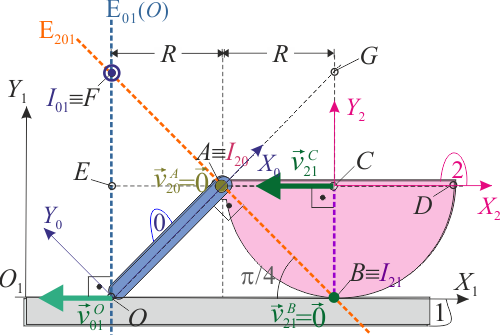
El semidisco de radio

R

y “centro”

C

(sólido “2”), y la barra

O A

de longitud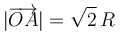 $|\overrightarrow{OA}|=\sqrt{2}\!\ R$ (sólido “0”) que se muestran en la figura, se mueven contenidos en todo momento en el plano fijo 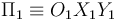$\Pi_1\equiv O_1X_1Y_1$ (sólido “1”). El extremo

A

de la barra se halla articulado en el extremo del diámetro

A C D

del semidisco, de manera que el punto del sólido “2” que ocupa la posición

A

se encuentra en reposo permanente respecto del sólido “0” (es decir, 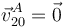$\vec{v}_{20}^A=\vec{0}$ en todo instante). El extremo

O

de la barra “0” desliza sobre la superficie horizontal que se corresponde con el eje

O 1 X 1

. Por su parte, el semidisco

2

mantiene un contacto puntual con la superficie horizontal que constituye el sólido “1” y que coincide con el eje

O 1 X 1

, por lo que su “centro”

C

se mantiene siempre a una distancia

R

de dicho eje, desplazándose con velocidad siempre paralela al mismo. En el instante considerado, el diámetro

A C D

esta colocado paralelo al eje

O 1 X 1

; el punto

C

se desplaza con velocidad

v 0

en el sentido negativo del eje

O 1 X 1

, a la vez que rueda sin deslizar en el punto correspondiente a la posición de contacto

B

(es decir, 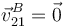$\vec{v}_{21}^B=\vec{0}$ ). Para dicho instante...

Indique las posiciones correspondientes a los C.I.R. de los movimientos {21}, {20} y {01}. Justifique su respuesta.
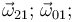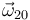Obtenga los vectores rotación instantánea $\vec{\omega}_{21}\mathrm{;}\;\vec{\omega}_{01}\mathrm{;}\,$ y $\, \vec{\omega}_{20}$ , y la velocidad con que desliza el extremo $O$ de la barra “0”

2 Solución

Introducción teórica

Un sólido rígido “ $i$ ” ( $τ i$ ), ejecuta un movimiento plano respecto de otro sólido “ $j$ ” ( $τ j$ ), cuando la reducción cinemática es de la forma:

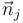$S_{ij}\equiv\left\{\begin{array}{l}\displaystyle \vec{\omega}_{ij}(t)=\omega (t)\!\ \vec{n}_j\\ \\ \displaystyle \vec{v}_{ij}^{\!\ O}(t)\,\perp\,\vec{n}_j\end{array}\right\}\;\; \Longrightarrow \;\; \vec{\omega}_{ij}(t)\cdot\vec{v}_{ij}^{\!\ O}(t)=0\mathrm{,}\;\;\forall\,t$

donde $\vec{n}_j$ es un vector unitario normal a un determinado plano $Π j$ , solidario con el sólido rígido $τ j$ respecto del que se describe el movimiento del sólido $τ i$ . Sin pérdida de generalidad, este plano se elige de manera que sea el plano donde se mueve y permanece el punto/posición $O$ , elegido(a) como centro de reducción del movimiento:

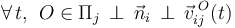
$\forall\,t\mathrm{,}\;\;O\in\Pi_j\,\perp\,\vec{n}_i\,\perp\,\vec{v}_{ij}^{\!\ O}(t)$

El plano $Π j$ es el plano director del movimiento plano { $i j$ }. En dicho movimiento, la trayectoria seguida por cualquier punto del sólido $τ i$ está contenida en el plano $Π j$ , o en otro plano paralelo a éste y, por tanto, también con el vector 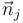$\vec{n}_j$ como dirección normal.

En el caso más general, un movimiento plano { $i j$ } consiste en un secuencia de rotaciones instantáneas en las que el vector rotación instantánea puede cambiar su módulo, pero mantiene su dirección constante, siempre perpendicular al plano $Π j$ (fijo en dicho movimiento). El eje de rotación $Δ i j$ , instantáneo o permanente, va a ser siempre perpendicular a los planos de movimiento (los que contienen las trayectorias de los diferentes puntos de sólido) y, en particular, al plano director $Π j$ . Como se sabe, este eje está constituido por todos los puntos del sólido “ $i$ ” que en el instante considerado tiene velocidad mínima. Y como el invariante escalar es nulo, el eje instantáneo de rotación está formado por aquellos puntos del sólido “ $i$ ” que en el instante considerado se hallan en reposo instantáneo (o permanente) respecto del sólido “ $j$ ”.

El punto de intersección del eje de rotación y el plano director se denomina centro instantáneo de rotación (C.I.R.).Obviamente, al pertenecer al eje instantáneo de rotación, el C.I.R. es el punto real o virtual del sólido “ $i$ ” que, en general, se mueve contenido en el plano director $Π j$ y que en el instante considerado se encuentra en reposo respecto del sólido “ $j$ ”.

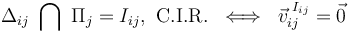
$\Delta_{ij}\ \bigcap\ \Pi_j=I_{ij}\mathrm{,}\;\;\mathrm{C.I.R.}\;\; \Longleftrightarrow \;\; \vec{v}_{ij}^{\!\ I_{ij}}=\vec{0}$

Durante la secuencia de rotaciones instantáneas que constituyen un movimiento plano, el eje instantáneo de rotaciación mantiene su dirección pero, en general, cambia su posición respecto el sólido en movimiento. Por tanto, en cada instante el C.I.R. se corresponde con un punto o posición distinta del sólido en movimiento, que puede ser adoptado como centro de reducción del movimiento instantáneo:

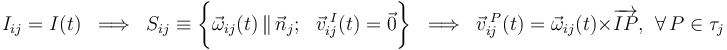
$I_{ij}=I(t)\;\; \Longrightarrow \;\;S_{ij}\equiv\bigg\{\vec{\omega}_{ij}(t)\,\|\,\vec{n}_j\mathrm{;}\;\;\;\vec{v}_{ij}^{\!\ I}(t)=\vec{0}\bigg\}\;\; \Longrightarrow \;\;\vec{v}_{ij}^{\!\ P}(t)=\vec{\omega}_{ij}(t)\times\overrightarrow{IP}\mathrm{,}\;\;\forall\,P\in\tau_j$

2.1 Posiciones de los C.I.R. de los movimientos relativos

El semidisco que denominamos sólido “2” y al barra $O A$ que constituye el sólido “0” se mueven contenidos en todo instante en el plano 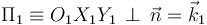$\Pi_1\equiv O_1X_1Y_1\,\perp\,\vec{n}=\vec{k}_1$ . Entonces, podemos definir sendos sistemas de referencia con solidarios con aquéllos sólidos, de manera que ambos tengan uno de sus ejes cartesianos siempre perpendicular al plano director $Π 1$ ; concretamente...

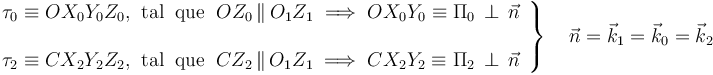
$\left.\begin{array}{l} \displaystyle \tau_0\equiv OX_0Y_0Z_0\mathrm{,}\;\;\mathrm{tal}\;\;\mathrm{que}\;\;OZ_0\,\|\, O_1Z_1\;\Longrightarrow\;OX_0Y_0\equiv\Pi_0\,\perp\, \vec{n}\\ \\ \displaystyle \tau_2\equiv CX_2Y_2Z_2\mathrm{,}\;\;\mathrm{tal}\;\;\mathrm{que}\;\;CZ_2\,\|\, O_1Z_1\;\Longrightarrow\;CX_2Y_2\equiv\Pi_2\,\perp\, \vec{n}\end{array}\right\}\quad\vec{n}=\vec{k}_1=\vec{k}_0=\vec{k}_2$

Los movimiento planos {21} y {01} se corresponden con el movimiento de los sólidos “2” y “0”, y en particular, de los planos $Π 2$ y $P i 0$ siempre contenidos en el plano $P i 1$ . El movimiento plano {20} es el movimiento relativo del plano $Π 2$ del semidisco, en el plano $Π 0$ al cual pertenece la barra rígida y que es paralelo a $Π 1$ y $Π 2$

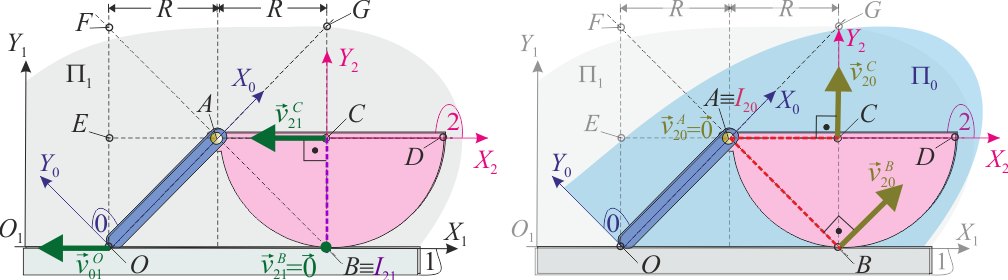
C.I.R. del movimiento {21}

En el enunciado se indica que, en el instante considerado el punto que ocupa la posición $C$ tiene velocidad no nula, mientras que el que ocupa la posición $B$ de contacto con el sólido “1” (solidario con el plano $Π 1$ ) rueda sin deslizar sobre la superficie del sólido “1” luego, por definición, su velocidad relativa respecto de “1” es nula. Por tanto, el C.I.R. correspondiente al movimiento {21}, en el instante considerado en la figura, se encuentra en dicha posición:

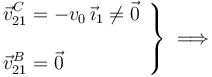
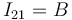
$\left.\begin{array}{l} \displaystyle \vec{v}_{21}^C=-v_0\!\ \vec{\imath}_1\neq\vec{0}\\ \\ \displaystyle \vec{v}_{21}^B=\vec{0} \end{array}\right\}\; \Longrightarrow$ $\displaystyle I_{21}=B$

El campo de velocidades del movimiento {21} en el instante considerado será de la forma...

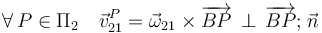
$\forall\, P\in\Pi_2\quad\vec{v}_{21}^P=\vec{\omega}_{21}\times\overrightarrow{BP}\,\perp\,\overrightarrow{BP}\mathrm{;}\;\vec{n}$

C.P.R. del movimiento {20}

Cuando el semidisco “2” realiza el movimiento plano respecto del plano $Π 0$ solidario con la barra “0”, el punto $A$ del semidisco permanece articulado en dicho extremo de la barra, es decir, en reposo permanente...

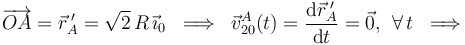
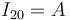
$\overrightarrow{OA}=\vec{r}_A^{\!\ \prime}=\sqrt{2}\!\ R\!\ \vec{\imath}_0\;\;\Longrightarrow\;\; \vec{v}_{20}^A(t)=\frac{\mathrm{d}\vec{r}_A^{\!\ \prime}}{\mathrm{d}t}=\vec{0}\mathrm{,}\;\;\forall\,t\;\;\Longrightarrow$ $\displaystyle I_{20}=A$

Los otros puntos del semidisco se pueden mover respecto de la barra, de manera que el campo de velocidades del movimiento {20} en el instante considerado será de la forma...

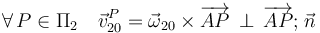
$\forall\, P\in\Pi_2\quad\vec{v}_{20}^P=\vec{\omega}_{20}\times\overrightarrow{AP}\,\perp\,\overrightarrow{AP}\mathrm{;}\;\vec{n}$

C.I.R. del movimiento {01}

En el caso del movimiento {01} sólo tenemos el dato de que el extremo $O$ de la barra desliza por el eje $O 1 X 1$ , y puesto que el campo de velocidades instantáneas de este movimiento, debe ser...

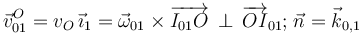
$\vec{v}_{01}^O=v_O\!\ \vec{\imath}_1=\vec{\omega}_{01}\times \overrightarrow{I_{01}O}\,\perp\,\overrightarrow{OI}_{01}\mathrm{;}\;\vec{n}=\vec{k}_{0,1}$

... podemos asegurar que el punto $I 01$ , C.I.R. del movimiento {01} en el instante considerado, debe estar en la recta $E 01 (O)$ , que pasa por el punto $O$ , y es perpendicular al vector 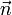$\vec{n}$ normal a los planos directores y a la dirección de la velocidad del punto $O$ en el movimiento y el instante considerado:

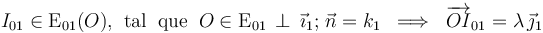
$I_{01}\in\mathrm{E}_{01}(O)\mathrm{,}\;\;\mathrm{tal}\;\;\mathrm{que}\;\;O\in\mathrm{E}_{01}\,\perp\,\vec{\imath}_1\mathrm{;}\;\vec{n}=k_1\;\;\Longrightarrow\;\; \overrightarrow{OI}_{01}=\lambda\!\ \vec{\jmath}_1$

donde $λ$ es un número de valor desconocido a priori. Para calcularlo y determinar la posición del $I 01$ , podemos aplicar el teorema de los tres centros que establece que cuando hay tres sólidos rígidos que realizan momientos planos relativos, todos ellos con planos directores coincidentes, los centros instantáneos (o permanentes) de rotación de los tres movimiento relativos están alineados en cada instante; es decir, en el sistema bajo estudio y en el instante considerado, podemos asegurar que existe una recta $E 201$ , definida por los puntos $B = I 21$ y $B = I 21$ , en la cual también se localiza el C.I.R. del movimiento {01}:

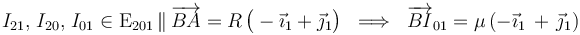
$I_{21}\mathrm{,}\;I_{20}\mathrm{,}\;I_{01}\in \mathrm{E}_{201}\,\|\,\overrightarrow{BA}=R\!\ \big(-\vec{\imath}_1+\vec{\jmath}_1\big)\;\;\Longrightarrow\;\; \overrightarrow{BI}_{01}=\mu\!\ (-\vec{\imath}_1\!\ +\!\ \vec{\jmath}_1)$

Y como el C.I.R. es único en cada instante y debe estar simultáneamente en las dos rectas descritas, va a ser el punto intersección de ambas: el punto denotado como $F$ en la figura. Analíticamente...

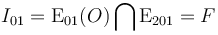
$I_{01}=\mathrm{E}_{01}(O)\bigcap \mathrm{E}_{201}=F$

Analíticamente...

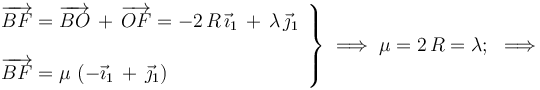
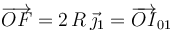
$\left.\begin{array}{l} \displaystyle \overrightarrow{BF}=\overrightarrow{BO}\!\ +\!\ \overrightarrow{OF}=-2\!\ R\!\ \vec{\imath}_1\!\ +\!\ \lambda\!\ \vec{\jmath}_1 \\ \\ \displaystyle \overrightarrow{BF}=\mu\!\ \left(-\vec{\imath}_1\!\ +\!\ \vec{\jmath}_1\right) \end{array}\right\}\;\Longrightarrow\;\mu=2\!\ R=\lambda\mathrm{;}\;\;\Longrightarrow$ $\overrightarrow{OF}=2\!\ R\!\ \vec{\jmath}_1=\overrightarrow{OI}_{01}$

2.2 Vectores rotación instantánea

Una vez determinada la posición de los centros de rotación, instantáneos o permanentes, de los tres movimientos plano relativos, basta con conocer la velocidad instantánea de algún punto para calcular facilmente el correspondiente vector rotación instantánea; para ello, sólo tenemos que aplicar la propiedad fundamental del campo de velocidades instantáneas del movimiento plano, tomando como centro de reducción la posión del C.I.R. en el instante considerado:

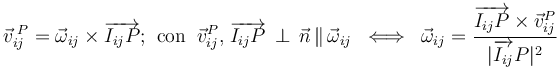
$\vec{v}_{ij}^{\!\ P}=\vec{\omega}_{ij}\times\overrightarrow{I_{ij}P}\mathrm{;}\;\;\mathrm{con}\;\;\vec{v}_{ij}^P\mathrm{,}\;\overrightarrow{I_{ij}P}\,\perp\,\vec{n}\,\|\,\vec{\omega}_{ij}\;\;\Longleftrightarrow\;\;\vec{\omega}_{ij}=\frac{\overrightarrow{I_{ij}P}\times\vec{v}_{ij}^P}{|\overrightarrow{I_{ij}}P|^2}$

Vector rotación en el movimiento {21}

Contamos con el dato de la velocidad del punto $C$ y que el $I 21$ está localizado en la posición $B$ de contacto del sólido rígido “2” con la superficie rígida de “1”:

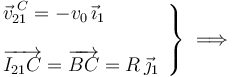
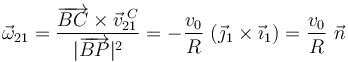
$\left.\begin{array}{l} \displaystyle \vec{v}_{21}^{\!\ C}=-v_0\!\ \vec{\imath}_1\\ \\ \displaystyle \overrightarrow{I_{21}C}=\overrightarrow{BC}=R\!\ \vec{\jmath}_1 \end{array}\right\}\;\Longrightarrow\;\;\;$ $\vec{\omega}_{21}=\frac{\overrightarrow{BC}\times\vec{v}_{21}^{\!\ C}}{|\overrightarrow{BP}|^2}=-\frac{v_0}{R}\ \big(\vec{\jmath}_1\times\vec{\imath}_1\big)=\frac{v_0}{R}\ \vec{n}$

Vector rotación del movimiento {01}

Conocemos la posición del $I 01$ y necesitamos conocer la velocidad de algún punto en este movimiento. Del extremo $O$ conocemos la dirección de la velocidad 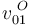$v_{01}^{\!\ O}$ , pero desconocemos sentido y módulo, por tanto no nos sirve. Sin embargo, podemos calcular el vector velocidad instantánea del otro extremo, aplicando las leyes de composición para movimientos relativos:

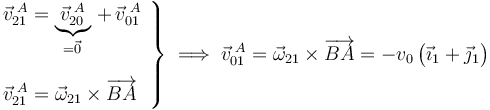
$\left.\begin{array}{l}\displaystyle \vec{v}_{21}^{\!\ A}=\underbrace{\vec{v}_{20}^{\!\ A}}_{=\vec{0}}\!\ +\!\ \vec{v}_{01}^{\!\ A} \\ \\ \displaystyle \vec{v}_{21}^{\!\ A}=\vec{\omega}_{21}\times\overrightarrow{BA} \end{array}\right\}\;\Longrightarrow\;\vec{v}_{01}^{\!\ A}=\vec{\omega}_{21}\times\overrightarrow{BA}=-v_0\!\ \big(\vec{\imath}_1+\vec{\jmath}_1\big)$

Calculamos también la posición relativa del punto $A$ respecto de la posición del $I 01$ en este instante, y que coincide con el punto $B$ :

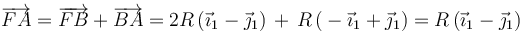
$\overrightarrow{FA}=\overrightarrow{FB}+\overrightarrow{BA}=2R\!\ \big(\vec{\imath}_1-\vec{\jmath}_1\big)\!\ +\!\ R\!\ \big(-\vec{\imath}_1+\vec{\jmath}_1\big)=R\!\ \big(\vec{\imath}_1-\vec{\jmath}_1\big)$

Y con estos resultados ya podemos calcular el vector rotación instantánea correspondiente al movimiento {01}:

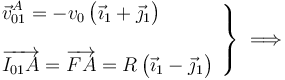
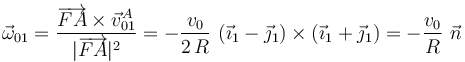
$\left.\begin{array}{l} \displaystyle \vec{v}_{01}^A=-v_0\!\ \big(\vec{\imath}_1+\vec{\jmath}_1\big)\\ \\ \displaystyle \overrightarrow{I_{01}A}=\overrightarrow{FA}=R\!\ \big(\vec{\imath}_1-\vec{\jmath}_1\big)\end{array}\right\}\;\Longrightarrow$ $\vec{\omega}_{01}=\frac{\overrightarrow{FA}\times\vec{v}_{01}^A}{|\overrightarrow{FA}|^2}=-\frac{v_0}{2\!\ R}\ \big(\vec{\imath}_1-\vec{\jmath}_1\big)\times \big(\vec{\imath}_1+\vec{\jmath}_1\big)=-\frac{v_0}{R}\ \vec{n}$

Vector rotación del movimiento {20}

Finalmente, para determinar el vector $\vec{\omega}_{20}$ aplicamos directamente la ley de composición para los vectores rotación instantánea de movimientos relativos:

$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\;\;\Longrightarrow$ $\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=\frac{2\!\ v_0}{R}\ \vec{n}$

Movimiento plano de semidisco y barra sobre plano fijo, F1 GIA (Ene, 2018)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posiciones de los C.I.R. de los movimientos relativos

2.2 Vectores rotación instantánea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES