Condensador plano paralelo (GIA)

De Laplace

(Diferencias entre revisiones)

Revisión de 18:26 15 jul 2018

1 Enunciado

Se tienen dos discos conductores idénticos, de radio 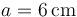$a=6\,\mathrm{cm}$ , con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica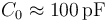 $C_0\approx100\,\mathrm{pF}$

Si los conductores están separados por aire, cuyo campo de ruptura es 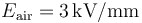$E_\mathrm{air}=3\,\mathrm{kV/mm}$ , ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
Si se separan por una lámina de papel de espesor 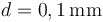$d=0,1\,\mathrm{mm}$ , cuya constante de dieléctrica es 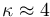$\kappa\approx 4$ , y cuyo campo de ruptura es 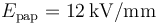$E_\mathrm{pap}=12\,\mathrm{kV/mm}$ , ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?

2 Solución

Introdución. El condensador plano-paralelo

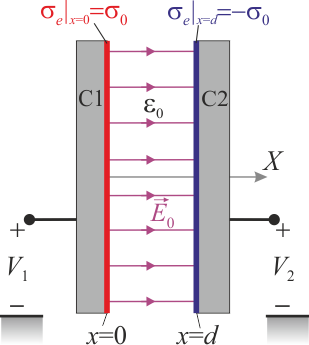
Un condensador plano paralelo es un sistema formado por dos superficies conductoras planas iguales, enfrentadas y dispuestas en sendos planos paralelos, separadas por un medio dieléctrico. Además, ambas superficies conductoras se están en influencia total: soportan cantidades opuestas de carga eléctrica y, por tanto, todas las líneas del campo eléctrico que “salen” del plano con carga positiva $+ Q$ , “terminan” en el plano con la carga negativa $- Q$ .

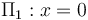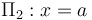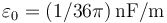Adoptaremos un sistema de referencia tal que los planos conductores enfrentados y cargados, coindicen con los planos geométricos $\displaystyle\Pi_1: x=0\;$ y $\;\displaystyle\Pi_2: x=a$ , ambos perpendiculares al eje $O X$ . Además, consideraremos que el dieléctrio que separa ambos planos es el vacío, cuya permitividad dieléctica en el Sistema Internacional de unidades es $\,\varepsilon_0=(1/36\pi)\,\mathrm{nF/m}$ .

En un condensador real con conductores de tamaño finito y planos en influencia total de área

S

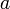, las cargas eléctricas se ditribuyen más o menos uniformemente en puntos alejados de los bordes de los planos condutores; los valores absolutos de las densidades de carga eléctrica crecen conforme nos aproximamos a dichos bordes. Sin embargo, si la distancia $\displaystyle a$ que separa los planos conductores es significativamente menor que las dimensiones de dichos plano, es posible despreciar estos efectos de borde y considerar, en primera aproximación, que las cargas eléctricas se distribuyen prácticamente uniformemente en los planos conductores, estando descritas por sendas densidades superficiales de carga constantes y opuestas:

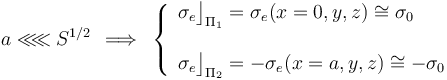
$a\ll\!\!\ll S^{1/2}\;\,\Longrightarrow\;\,\left\{\begin{array}{l}\sigma_e\big\rfloor_{\Pi_1}=\sigma_e(x=0,y,z)\cong\sigma_0\\ \\ \sigma_e\big\rfloor_{\Pi_2}=-\sigma_e(x=a,y,z)\cong-\sigma_0\end{array}\right.$

En consecuencia, las cantidades opuestas de carga distribuidas en los planos conductores serán:

$\begin{array}{l}\displaystyle Q\big\rfloor_{\Pi_1}=\int_{\Pi_1}\!\!\sigma_e\ \mathrm{d}S\cong\sigma_0\ S=+Q\\ \\ \displaystyle Q\big\rfloor_{\Pi_2}=\int_{\Pi_2}\!\!\sigma_e\ \mathrm{d}S\cong-\sigma_0\ S=-Q\end{array}$

Como pudo comprobarse en el ejercicio dedicado al estudio del campo eléctrico creado por planos cargados uniformemente, dos distribuciones superficiales de carga constantes y opuestas, localizadas en dos planos paralelos enfrentados separadas por vacío, sólo crean campo eléctrico en los puntos situados entre los planos. Y éste es uniforme, perpendicular a los planos cargados y de módulo proporcional al valor absoluto de la densidad constante de carga. En el caso que nos ocupa, se tendrá que...

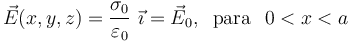
$\vec{E}(x,y,z)=\frac{\sigma_0}{\varepsilon_0}\ \vec{\imath}=\vec{E}_0\mathrm{,}\;\;\,\mathrm{para}\,\;\; 0< x< a$

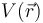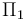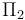Este campo eléctrico implica la existencia de un potencial electrostático $V(\vec{r})$ , en el que las superficies conductoras son superficies equipotenciales. La diferencia de potencial entre ambas es igual a la circulación del campo entre sendos puntos de dichos conductores. Si se calcula a lo largo de una línea cuyos puntos estén todos situados entre los planos $\displaystyle \Pi_1$ y $\displaystyle \Pi_2$ , se tendrá:

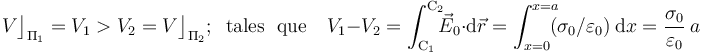
$V\big\rfloor_{\Pi_1}=V_1>V_2=V\big\rfloor_{\Pi_2}\mathrm{;}\;\;\,\mathrm{tales}\,\;\,\mathrm{que}\,\;\;\; V_1-V_2=\int_{\mathrm{C}_1}^{\mathrm{C}_2}\!\!\!\vec{E}_0\cdot\mathrm{d}\vec{r}=\int_{x=0}^{x=a}\!\!\!(\sigma_0/\varepsilon_0)\ \mathrm{d}x=\frac{\sigma_0}{\varepsilon_0}\ a$

Capacidad eléctrica de un condensador

Las propiedades eléctricas y el comportamient de un condensador en un circuito están caracterizadas por su capacidad eléctrica C, definida como la relación entre la carga eléctrica que se distribuye en uno de sus conductores y la diferencia de potencial entre éste y el otro conductor. Se trata de un parámetro que depende de la geometría del sistema(forma de los conductores, posición relativa,...) y del medio dieléctrico que se interpone entre los conductores. En el caso del condensador plano paralelo analizado, con espacio vacío entre los conductores, se tendrá:

$C_0=\frac{Q\big\rfloor_{\Pi_1}}{V\big\rfloor_{\Pi_1}-V\big\rfloor_{\Pi_2}}=\frac{Q}{V_1-V_2}\;\;\Longrightarrow\;\;$ $C_0\approx \frac{\sigma_0\ S}{(\sigma_0/\varepsilon_0)\ a}=\frac{\varepsilon_0\ S}{a}$

Revisión de 18:21 15 jul 2018 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Solución) ← Edición más antigua		Revisión de 18:26 15 jul 2018 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Solución) Edición más nueva →
Línea 34:		Línea 34:
	Las propiedades eléctricas y el comportamient de un condensador en un circuito están caracterizadas por su '''capacidad eléctrica''' ''C'', definida como la relación entre la carga eléctrica que se distribuye en uno de sus conductores y la diferencia de potencial entre éste y el otro conductor. Se trata de un parámetro que depende de la geometría del sistema(forma de los conductores, posición relativa,...) y del medio dieléctrico que se interpone entre los conductores. En el caso del condensador plano paralelo analizado, con espacio vacío entre los conductores, se tendrá:		Las propiedades eléctricas y el comportamient de un condensador en un circuito están caracterizadas por su '''capacidad eléctrica''' ''C'', definida como la relación entre la carga eléctrica que se distribuye en uno de sus conductores y la diferencia de potencial entre éste y el otro conductor. Se trata de un parámetro que depende de la geometría del sistema(forma de los conductores, posición relativa,...) y del medio dieléctrico que se interpone entre los conductores. En el caso del condensador plano paralelo analizado, con espacio vacío entre los conductores, se tendrá:

-	<center><math>C_0=\frac{Q\big\rfloor_{\Pi_1}}{V\big\rfloor_{\Pi_1}-V\big\rfloor_{\Pi_2}}=\frac{Q}{V_1-V_2}\;\;\Longrightarrow\;\;</math><math>C_0\approx \frac{\sigma_0\ S}{(\sigma_0/\varepsilon_0)\ a}=\frac{\varepsilon_0\ S}{a}</math></center>	+	<center><math>C_0=\frac{Q\big\rfloor_{\Pi_1}}{V\big\rfloor_{\Pi_1}-V\big\rfloor_{\Pi_2}}=\frac{Q}{V_1-V_2}\;\;\Longrightarrow\;\;</math><math style="border:solid blue 2px;padding:10px">C_0\approx \frac{\sigma_0\ S}{(\sigma_0/\varepsilon_0)\ a}=\frac{\varepsilon_0\ S}{a}</math></center>

Condensador plano paralelo (GIA)

De Laplace

Revisión de 18:26 15 jul 2018

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES