Movimientos rígidos (CMR)
De Laplace
(→Campo de velocidades) |
(→Campo de aceleraciones) |
||
| (43 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==El modelo del sólido rígido== | ==El modelo del sólido rígido== | ||
===Condición geométrica de rigidez=== | ===Condición geométrica de rigidez=== | ||
| - | + | [[Archivo:movimiento-solido-esfera.gif|right]] | |
| - | + | ||
| - | + | Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto <math>A_0</math> y posteriormente en el punto <math>A</math> y lo mismo con partículas B, C,… se cumple en todo instante | |
| - | Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto <math>A_0</math> y posteriormente en el punto <math>A</math> y lo mismo | + | |
<center><math>\left|\overrightarrow{AB}\right| = \left|\overrightarrow{A_0B_0}\right|</math></center> | <center><math>\left|\overrightarrow{AB}\right| = \left|\overrightarrow{A_0B_0}\right|</math></center> | ||
| Línea 12: | Línea 11: | ||
<center><math>\overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{A_0B_0}\cdot\overrightarrow{A_0C_0}</math></center> | <center><math>\overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{A_0B_0}\cdot\overrightarrow{A_0C_0}</math></center> | ||
| - | + | ===Condición cinemática de rigidez=== | |
| + | Cada ligadura geométrica implica una relación entre las velocidades posibles, ya que si la distancia entre un par de partículas es constante, no puede ser que sus velocidades nos digan que se están acercando o alejando. Obtenemos estas relaciones derivando en la expresión de los vínculos geométricos. | ||
| - | + | Elevando al cuadrado | |
| - | <center><math>\ | + | <center><math>\left(\vec{r}_B-\vec{r}_A\right)\cdot\left(\vec{r}_B-\vec{r}_A\right)=|\overrightarrow{AB}|^2 =\mathrm{cte}</math></center> |
| - | + | y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades. | |
| - | + | <center><math>0 = 2\left(\frac{\mathrm{d}\vec{r}_B}{\mathrm{d}t}-\frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}\right)\cdot\left(\vec{r}_B-\vec{r}_A\right)=2\left(\vec{v}_B-\vec{v}_A\right)\cdot\left(\vec{r}_B-\vec{r}_B\right)</math></center> | |
| - | + | Esta es la '''condición cinemática de rigidez''', | |
| + | <center><math> | ||
| + | \left(\vec{v}_B-\vec{v}_A\right)\cdot\left(\vec{r}_B-\vec{r}_A\right) = (\vec{v}_B-\vec{v}_A)\cdot\overrightarrow{AB}=0</math></center> | ||
| - | + | Esta condición nos dice que la velocidad relativa del punto B respecto del A (esto es, la que mide un observador situado en A y moviéndose con este punto) es ortogonal al vector de posición relativa | |
| - | + | ||
| - | + | <center><math>(\vec{v}_B-\vec{v}_{A})\perp \overrightarrow{AB}</math></center> | |
| - | + | Esta condición cinemática se puede visualizar. Si estamos solidariamente unidos al punto A, vemos al punto B siempre a la misma distancia, es decir, se encuentra sobre la superficie de una esfera imaginaria. Al moverse sobre la esfera, su velocidad es tangente a la superficie y perpendicular al radio, que es el vector de posición relativo. Por tanto la velocidad relativa y la posición relativa son ortogonales. | |
| - | + | <center>[[Archivo:velocidad-relativa-solido.png]]</center> | |
| - | + | La condición cinemática la podemos escribir también como | |
| - | + | ||
| - | <center><math>\vec{ | + | <center><math>\vec{v}_B\cdot(\vec{r}_B-\vec{r}_A) = \vec{v}_A\cdot(\vec{r}_B-\vec{r}_A)</math></center> |
| - | + | o, empleando el vector de posición relativo | |
| - | + | ||
| - | <center><math>\ | + | <center><math>\vec{v}_A\cdot\overrightarrow{AB}=\vec{v}_B\cdot\overrightarrow{AB}</math></center> |
| - | a la | + | Introduciendo el vector unitario en la dirección del segmento que une los dos puntos y en el sentido de la partícula A a la B. |
| - | <center><math>\overrightarrow{ | + | <center><math>\vec{u}_{AB}=\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} = \frac{\vec{r}_B-\vec{r}_A}{|\vec{r}_B-\vec{r}_A|}</math></center> |
| - | + | [[Archivo:velocidad-equiproyectiva.png|right]] | |
| - | + | queda | |
| - | + | <center><math>\vec{v}_B\cdot\vec{u}_{AB}=\vec{v}_A\cdot\vec{u}_{AB}</math></center> | |
| - | <center><math>\overrightarrow{ | + | <!-- |
| + | <center><math>\vec{v}^A\cdot\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\vec{v}^B\cdot\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}</math></center> | ||
| + | --> | ||
| + | siendo cada miembro la proyección de la velocidad en la dirección del vector <math>\vec{u}_{ik}</math> | ||
| - | + | <center><math>\mathrm{proy}_{\parallel \vec{u}_{AB}}(\vec{v}_B)=\mathrm{proy}_{\parallel\vec{u}_{AB}}(\vec{v}_A)</math></center> | |
| - | < | + | La condición cinemática de rigidez implica que, dadas dos partículas, <math>A</math> y <math>B</math>, la proyección de sus respectivas velocidades sobre la recta que las une es la misma. Por ello se dice que el campo de velocidades es ''equiproyectivo''. |
| - | |||
| - | + | El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa. | |
| - | + | ==Sólidos y sistemas de referencia== | |
| + | [[Archivo:solido-extension-indefinida.png|right]] | ||
| - | y | + | Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales. |
| - | + | Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a ''todo'' el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad. | |
| - | + | ||
| - | + | ||
| - | + | Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido. | |
| - | + | Podemos abreviar este principio básico con unas simples siglas: | |
| - | + | <center>[[Archivo:srsr.png|300px]]</center> | |
| - | + | ==Grados de libertad de un sólido== | |
| + | El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema. | ||
| - | + | ¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos. | |
| - | + | Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas. | |
| - | + | {| class="bordeado" | |
| + | |- | ||
| + | | [[Archivo:solido-1-particula.png|240px]] | ||
| + | | [[Archivo:solido-2-particulas.png|240px]] | ||
| + | | [[Archivo:solido-3-particulas.png|240px]] | ||
| + | |} | ||
| - | + | Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio <math>d_{12}</math> alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo). | |
| - | + | ||
| - | < | + | Una tercera partícula se encuentra a una distancia <math>d_{13}</math> de la primera y a una distancia <math>d_{23}</math> de la segunda. La posición de esta tercera partícula se encuentra por tanto sobre la circunferencia intersección de una esfera de radio <math>d_{13}</math> alrededor de la primera y una esfera de radio <math>d_{23}</math> alrededor de la segunda, y para localizar una posición concreta sobre una circunferencia solo necesitamos 1 variable. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales. | |
| - | + | Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido. | |
| - | + | En términos geométricos, mientras que una partícula solo posee los grados de libertad correspondientes a 3 traslaciones independientes (en la dirección de OX, de OY y de oZ, por ejemplo), un sólido incorpora además 3 posibles rotaciones respecto a ejes diferentes, resultando un total de 3 + 3 = 6 grados de libertad. | |
| - | : | + | <center>[[Archivo:grados-libertad-solido.png]]</center> |
| + | Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6. | ||
| - | + | ==Movimientos rígidos== | |
| + | Existen diferentes transformaciones que mantienen las distancias y los ángulos: | ||
| - | + | ;Traslaciones: Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido | |
| - | + | <center><math>\overrightarrow{A_0A}=\overrightarrow{B_0B}\qquad\qquad \overrightarrow{A_2B_2} = \overrightarrow{AB}</math></center> | |
| - | + | ;Rotaciones: Existe al menos un punto cuya posición no se ve modificada. El resto de puntos experimenta un desplazamiento perpendicular a dicho eje. | |
| - | + | ||
| - | + | ;Simetría: Se invierten las posiciones respecto a un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo. | |
| - | + | Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación. | |
| - | + | Para ello consideramos un partícula del sólido que inicialmente se hallaba en <math>A_0</math> y posteriormente en <math>A</math>. Este punto experimenta un desplazamiento | |
| + | <center><math>\Delta\vec{r}=\overrightarrow{A_0A}</math></center> | ||
| - | + | Supongamos que sometemos a todo el sólido a una traslación <math>\Delta\vec{r}</math>. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que <math>A</math> es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A. | |
| + | <center>[[Archivo:tras-rot.png|577px]]</center> | ||
| - | + | ==Traslaciones== | |
| + | {{ac|Traslaciones de un sólido rígido}} | ||
| + | ==Rotaciones== | ||
| + | {{ac|Rotaciones de un sólido rígido}} | ||
| + | ==Movimiento general de un sólido== | ||
| + | {{ac|Movimiento general de un sólido rígido}} | ||
| - | + | ==Campo de aceleraciones== | |
| + | {{ac|Campo de aceleraciones de un sólido}} | ||
| - | + | ==Movimiento plano== | |
| + | {{ac|Movimiento plano de un sólido}} | ||
| - | + | [[Categoría:Cinemática del sólido rígido (CMR)]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[Categoría: | + | |
última version al 17:47 2 nov 2017
Contenido |
1 El modelo del sólido rígido
1.1 Condición geométrica de rigidez
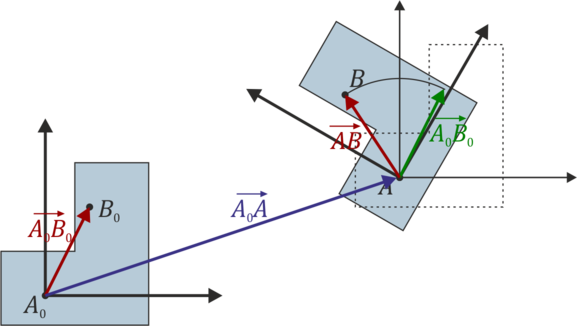
Un movimiento rígido de un sólido es aquel que preserva las distancias entre cada par de puntos, de forma que si una partícula se encuentra inicialmente en el punto A0 y posteriormente en el punto A y lo mismo con partículas B, C,… se cumple en todo instante
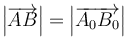
y al cumplirse para todos los puntos esto implica igualmente la conservación de los ángulos
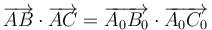
1.2 Condición cinemática de rigidez
Cada ligadura geométrica implica una relación entre las velocidades posibles, ya que si la distancia entre un par de partículas es constante, no puede ser que sus velocidades nos digan que se están acercando o alejando. Obtenemos estas relaciones derivando en la expresión de los vínculos geométricos.
Elevando al cuadrado
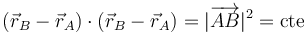
y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades.
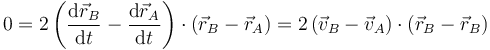
Esta es la condición cinemática de rigidez,
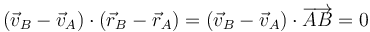
Esta condición nos dice que la velocidad relativa del punto B respecto del A (esto es, la que mide un observador situado en A y moviéndose con este punto) es ortogonal al vector de posición relativa
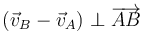
Esta condición cinemática se puede visualizar. Si estamos solidariamente unidos al punto A, vemos al punto B siempre a la misma distancia, es decir, se encuentra sobre la superficie de una esfera imaginaria. Al moverse sobre la esfera, su velocidad es tangente a la superficie y perpendicular al radio, que es el vector de posición relativo. Por tanto la velocidad relativa y la posición relativa son ortogonales.
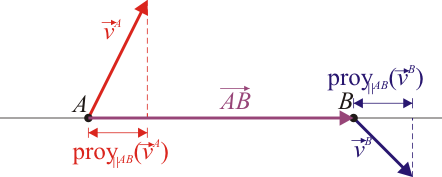
La condición cinemática la podemos escribir también como
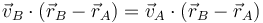
o, empleando el vector de posición relativo
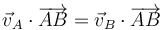
Introduciendo el vector unitario en la dirección del segmento que une los dos puntos y en el sentido de la partícula A a la B.
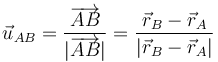
queda
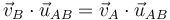
siendo cada miembro la proyección de la velocidad en la dirección del vector 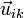
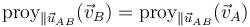
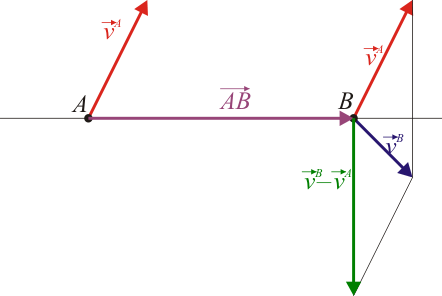
La condición cinemática de rigidez implica que, dadas dos partículas, A y B, la proyección de sus respectivas velocidades sobre la recta que las une es la misma. Por ello se dice que el campo de velocidades es equiproyectivo.
El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa.
2 Sólidos y sistemas de referencia
Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales.
Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a todo el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad.
Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido.
Podemos abreviar este principio básico con unas simples siglas:

3 Grados de libertad de un sólido
El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema.
¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos.
Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas.
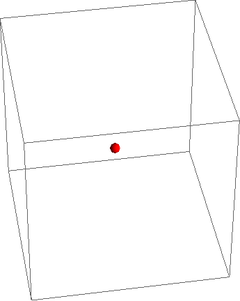
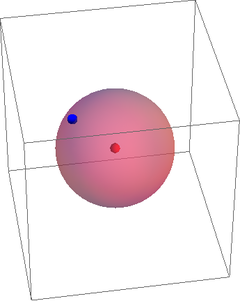
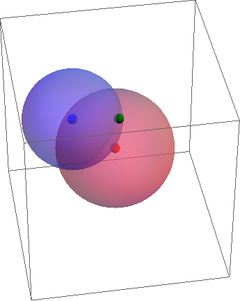
| 
| 
|
Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio d12 alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo).
Una tercera partícula se encuentra a una distancia d13 de la primera y a una distancia d23 de la segunda. La posición de esta tercera partícula se encuentra por tanto sobre la circunferencia intersección de una esfera de radio d13 alrededor de la primera y una esfera de radio d23 alrededor de la segunda, y para localizar una posición concreta sobre una circunferencia solo necesitamos 1 variable.
Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales.
Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido.
En términos geométricos, mientras que una partícula solo posee los grados de libertad correspondientes a 3 traslaciones independientes (en la dirección de OX, de OY y de oZ, por ejemplo), un sólido incorpora además 3 posibles rotaciones respecto a ejes diferentes, resultando un total de 3 + 3 = 6 grados de libertad.
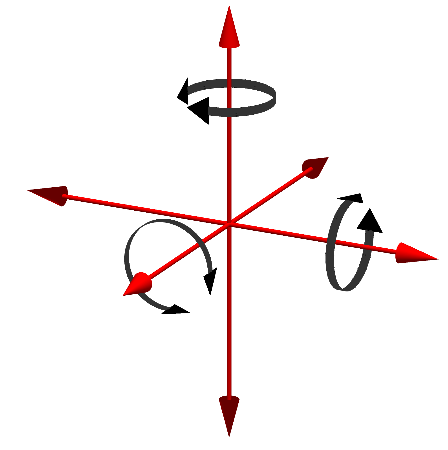
Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6.
4 Movimientos rígidos
Existen diferentes transformaciones que mantienen las distancias y los ángulos:
- Traslaciones
- Todos los puntos experimentan el mismo desplazamiento, preservándose la orientación del sólido

- Rotaciones
- Existe al menos un punto cuya posición no se ve modificada. El resto de puntos experimenta un desplazamiento perpendicular a dicho eje.
- Simetría
- Se invierten las posiciones respecto a un plano de simetría. Un movimiento real de un sólido nunca puede consistir en una simetría (debería “volverse del revés”) por lo que no las consideremos en este artículo.
Un teorema crucial en la cinemática del sólido es que todo movimiento real puede descomponerse en una traslación y una rotación.
Para ello consideramos un partícula del sólido que inicialmente se hallaba en A0 y posteriormente en A. Este punto experimenta un desplazamiento
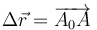
Supongamos que sometemos a todo el sólido a una traslación 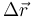 . para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A.
. para pasar de este estado intermedio al estado final debemos efectuar otro movimiento rígido en el que A es un punto fijo (porque ya se ha movido todo lo que se tenía que mover). Este segundo movimiento será entonces una rotación alrededor de A.