Movimiento general de un sólido rígido
De Laplace
(Página creada con '==Movimientos finitos== ==Campo de velocidades== ===Propiedades generales=== ===Clasificación de movimientos=== Categoría:Cinemática del sólido rígido (CMR)') |
|||
| Línea 1: | Línea 1: | ||
==Movimientos finitos== | ==Movimientos finitos== | ||
| + | El caso general de movimiento de un sólido es una composición de una rotaci´´on seguida de una traslación (o viceversa). | ||
| + | |||
| + | El procedimiento es simple. Elegimos un punto <math>O_0</math> del sólido y efectuamos una rotación alrededor del punto hasta que la orientación del sólido coincide con la del estado final. A continuación trasladamos el sólido hasta que coincide con su ubicación definitiva. | ||
| + | |||
| + | En forma vectorial, es movimiento para cada punto será | ||
| + | |||
| + | <center><math>x\vec{\imath}_1+y\vec{\jmath}_1+z\vec{k}_1=\left(\Delta x_O\vec{\imath}_1+\Delta y_O\vec{\jmath}_1+\Delta z_O\vec{k}_1\right)+\left(X\vec{\imath}_2+Y\vec{\jmath}_2+Z\vec{k}_2\right)</math></center> | ||
| + | |||
| + | o, en forma matricial | ||
| + | |||
| + | <center><math>\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}\Delta x_O\\ \Delta y_O\\ \Delta z_O\end{pmatrix}+\begin{pmatrix} R_{XX} & R_{XY} & R_{ZZ} \\ | ||
| + | R_{YX} & R_{YY} & R_{YZ} \\ R_{XZ} & R_{YZ} & R_{ZZ} \end{pmatrix}\cdot \begin{pmatrix}X \\ Y \\ Z\end{pmatrix}</math></center> | ||
| + | |||
| + | El punto <math>O_0</math> no tiene nada de particular. Podemos elegir cualquier otro punto para efectuar la rotación inicial. Dependiendo del punto que elijamos la traslación será diferente, pero la rotación será la misma sea cual sea el centro de reducción. | ||
| + | |||
| + | Chasles generalizó el teorema de Euler, observando que ese desplzamiento arbitrario puede descomponerse en una traslación paralela al eje de rotación y en una ortogonal a él. la parte ortogonal puede englobarse en la rotación, quedando solo la paralela. | ||
| + | |||
| + | Por tanto, el movimiento general de un sólido se reduce a una rotación en torno a un eje y un desplazamiento en la dirección de este eje (que en este contexto se denomina ''eje de rotación y mínimo deslizamiento''). Este movimiento se denomina “un tornillo” por su analogía con la conducta de esta herramienta. | ||
| + | |||
==Campo de velocidades== | ==Campo de velocidades== | ||
| + | Cuando un sólido rígido se mueve efectúa en cada instante un movimiento rígido infinitesimal. | ||
| + | |||
| + | Como en los movimientos finitos, consideraremos dos sistemas de referencia: el 1, que consideramos como fijo y el 2, ligado al sólido. | ||
| + | |||
| + | Dado que un punto P del espacio puede considerarse simultáneamente como parte del sistema de referencia 1 y como parte del sistema 2, emplearemos la siguiente notación para indicar la velocidad del punto P | ||
| + | |||
| + | <center>[[Archivo:vP21.png]]</center> | ||
| + | |||
| + | Esta notación puede parece un poco excesiva en este contexto, pero será de gran utilidad al considerar el [[Cinemática_del_movimiento_relativo_(CMR)|movimiento relativo]]. | ||
| + | |||
| + | De acuerdo con el teorema de Chasles, este movimiento instantáneo se compondrá de una rotación diferencial alrededor de un eje (que ahora será eje ''instantáneo'' de rotación y mínimo deslizamiento, ya que puede cambiar de un instante a otro) y de un desplazamiento. | ||
| + | |||
| + | Si tomamos como referencia el punto O (“centro de reducción”) la velocidad de cualquier punto será la suma vectorial de la traslación de O más la rotación alrededor de un eje que pasa por O. | ||
| + | |||
| + | Para la velocidad de la rotación no tenemos más que considerar de nuevo qué le ocurre a la base ligada al sólido. | ||
| + | |||
| + | Si consideramos un punto P del sólido, su expresión en la bae ligada al sólido será | ||
| + | |||
| + | <center><math>\overrightarrow{OP}=x_2\vec{\imath}_2+y_2\vec{\jmath}_2+z_2\vec{k}_2</math></center> | ||
| + | |||
| + | Este vector será constante en el sistema de referencia ligado al sólido, pero no en el sistema fijo 1. Si derivamos esta expresión en el sistema de referencia 1, solo son dependientes del tiempo los vectores de la base | ||
| + | |||
| + | <center><math>\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OP}\right|_1=x_2\left.\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}\right|_1+y_2\left.\frac{\mathrm{d}\vec{\jmath}_2}{\mathrm{d}t}\right|_1+z_2\left.\frac{\mathrm{d}\vec{k}_2}{\mathrm{d}t}\right|_1</math></center> | ||
| + | |||
| + | ¿Cuánto vale la derivada respecto al tiempo de <math>\vec{\imath}_2</math>? El extremo de este vector está realizando un movimiento circular instantáneo alrededor del eje de rotación y por tanto su velocidad cumple la relación | ||
| + | |||
| + | <center><math>\left.\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}\right|_1=\vec{\omega}_{21}\times \vec{\imath}_2</math></center> | ||
| + | |||
| + | y lo mismo para los otros dos vectores de la base, que giran con la misma velocidad angular (si las velocidades angulares fueran diferentes el sólido dejaría de ser rígido, ya que los vectores de la base se acercarían o alejarían). Por tanto, | ||
| + | |||
| + | <center><math>\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OP}\right|_1=x_2(\vec{\omega}_{21}\times \vec{\imath}_2)+y_2(\vec{\omega}_{21}\times \vec{\jmath}_2)+z_2(\vec{\omega}_{21}\times \vec{k}_2)=\vec{\omega}_{21}\times(x_2\vec{\imath}_2+y_2\vec{\jmath}_2+z_2\vec{k}_2)=\vec{\omega}_{21}\times\overrightarrow{OP}</math></center> | ||
| + | |||
| + | <center>[[Archivo:rotación-instantanea-base.png|600px]]</center> | ||
| + | Por tanto, la velocidad debida a la rotación del sólido será, para todos los puntos, | ||
| + | |||
| + | <center><math>\vec{v}_{21}^{Pr}=\vec{\omega}_{21}\times\overrightarrow{OP}</math></center> | ||
| + | |||
| + | Aquí al vector <math>\vec{\omega}_{21}</math> se lo denomina ''vector rotación'' del sólido o velocidad angular instantánea del sólido. El criterio para asignar los subíndices es el mismo que para la velocidad lineal | ||
| + | |||
| + | <center>[[Archivo:w21.png]]</center> | ||
| + | |||
| + | A esta velocidad habrá que sumarle la de la traslación del punto O, que será común para todos los puntos | ||
| + | |||
| + | <center><math>\vec{v}_{21}^{Pt}=\vec{v}^O_{21}</math></center> | ||
| + | |||
| + | y por tanto la velocidad de cualquier punto del sólido es de la forma | ||
| + | |||
| + | <center><math>\vec{v}^P_{21}=\vec{v}^O_{21}+\vec{\omega}_{21}\times \overrightarrow{OP}</math></center> | ||
| + | |||
| + | ===Cambio del centro de reducción=== | ||
| + | En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos | ||
| + | |||
| + | <center><math>\vec{v}^P_{21}=\vec{v}^O_{21}+\vec{\omega}_{21}\times\left(\overrightarrow{OA}+\overrightarrow{AP}\right)=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AP}</math></center> | ||
| + | |||
| + | es, decir, para cualquier par de puntos se cumple | ||
| + | |||
| + | <center><math>\vec{v}^P_{21}=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AP}</math></center> | ||
| + | |||
| + | o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par <math>\{\vec{\omega}_{21},\vec{v}^A_{21}\}</math> se lo denomina ''reducción cinemática'' del campo de velocidades en el punto A. | ||
===Propiedades generales=== | ===Propiedades generales=== | ||
===Clasificación de movimientos=== | ===Clasificación de movimientos=== | ||
[[Categoría:Cinemática del sólido rígido (CMR)]] | [[Categoría:Cinemática del sólido rígido (CMR)]] | ||
Revisión de 15:58 31 oct 2017
Contenido |
1 Movimientos finitos
El caso general de movimiento de un sólido es una composición de una rotaci´´on seguida de una traslación (o viceversa).
El procedimiento es simple. Elegimos un punto O0 del sólido y efectuamos una rotación alrededor del punto hasta que la orientación del sólido coincide con la del estado final. A continuación trasladamos el sólido hasta que coincide con su ubicación definitiva.
En forma vectorial, es movimiento para cada punto será
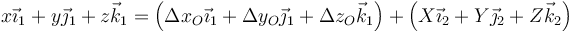
o, en forma matricial
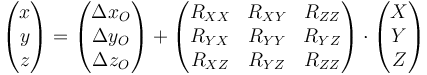
El punto O0 no tiene nada de particular. Podemos elegir cualquier otro punto para efectuar la rotación inicial. Dependiendo del punto que elijamos la traslación será diferente, pero la rotación será la misma sea cual sea el centro de reducción.
Chasles generalizó el teorema de Euler, observando que ese desplzamiento arbitrario puede descomponerse en una traslación paralela al eje de rotación y en una ortogonal a él. la parte ortogonal puede englobarse en la rotación, quedando solo la paralela.
Por tanto, el movimiento general de un sólido se reduce a una rotación en torno a un eje y un desplazamiento en la dirección de este eje (que en este contexto se denomina eje de rotación y mínimo deslizamiento). Este movimiento se denomina “un tornillo” por su analogía con la conducta de esta herramienta.
2 Campo de velocidades
Cuando un sólido rígido se mueve efectúa en cada instante un movimiento rígido infinitesimal.
Como en los movimientos finitos, consideraremos dos sistemas de referencia: el 1, que consideramos como fijo y el 2, ligado al sólido.
Dado que un punto P del espacio puede considerarse simultáneamente como parte del sistema de referencia 1 y como parte del sistema 2, emplearemos la siguiente notación para indicar la velocidad del punto P
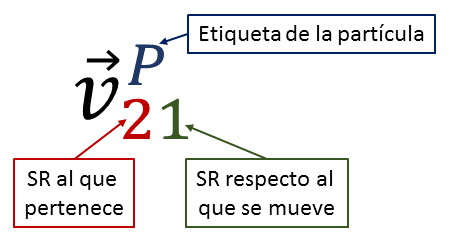
Esta notación puede parece un poco excesiva en este contexto, pero será de gran utilidad al considerar el movimiento relativo.
De acuerdo con el teorema de Chasles, este movimiento instantáneo se compondrá de una rotación diferencial alrededor de un eje (que ahora será eje instantáneo de rotación y mínimo deslizamiento, ya que puede cambiar de un instante a otro) y de un desplazamiento.
Si tomamos como referencia el punto O (“centro de reducción”) la velocidad de cualquier punto será la suma vectorial de la traslación de O más la rotación alrededor de un eje que pasa por O.
Para la velocidad de la rotación no tenemos más que considerar de nuevo qué le ocurre a la base ligada al sólido.
Si consideramos un punto P del sólido, su expresión en la bae ligada al sólido será
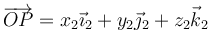
Este vector será constante en el sistema de referencia ligado al sólido, pero no en el sistema fijo 1. Si derivamos esta expresión en el sistema de referencia 1, solo son dependientes del tiempo los vectores de la base
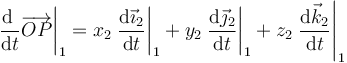
¿Cuánto vale la derivada respecto al tiempo de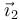 
? El extremo de este vector está realizando un movimiento circular instantáneo alrededor del eje de rotación y por tanto su velocidad cumple la relación
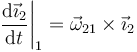
y lo mismo para los otros dos vectores de la base, que giran con la misma velocidad angular (si las velocidades angulares fueran diferentes el sólido dejaría de ser rígido, ya que los vectores de la base se acercarían o alejarían). Por tanto,
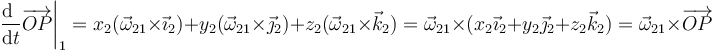
| Error al crear miniatura: |
Por tanto, la velocidad debida a la rotación del sólido será, para todos los puntos,
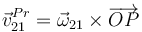
Aquí al vector 
se lo denomina vector rotación del sólido o velocidad angular instantánea del sólido. El criterio para asignar los subíndices es el mismo que para la velocidad lineal
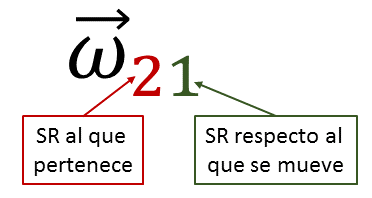
A esta velocidad habrá que sumarle la de la traslación del punto O, que será común para todos los puntos
y por tanto la velocidad de cualquier punto del sólido es de la forma
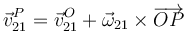
2.1 Cambio del centro de reducción
En un movimiento general, sin punto fijo, el punto O no tiene nada de especial. Si consideramos como referencia otro punto A obtenemos
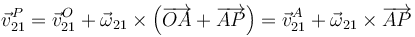
es, decir, para cualquier par de puntos se cumple
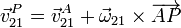
o dicho de otra forma, para conocer la velocidad instantánea de cualquier punto basta con conocer la velocidad angular (misma para todos) y la velocidad de un punto cualquiera. Al par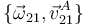 
se lo denomina reducción cinemática del campo de velocidades en el punto A.
