De Laplace
(Diferencias entre revisiones)
|
|
| (6 ediciones intermedias no se muestran.) |
| Línea 3: |
Línea 3: |
| | | | |
| | [[F1 GIA SPC 2013, Satélite girando alrededor de la Tierra | Satélite girando alrededor de la Tierra]] | | [[F1 GIA SPC 2013, Satélite girando alrededor de la Tierra | Satélite girando alrededor de la Tierra]] |
| | + | |
| | | | |
| | [[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] | | [[F1 GIA SPC 2013, Disco rotando alrededor de barra vertical | Disco rotando alrededor de barra vertical]] |
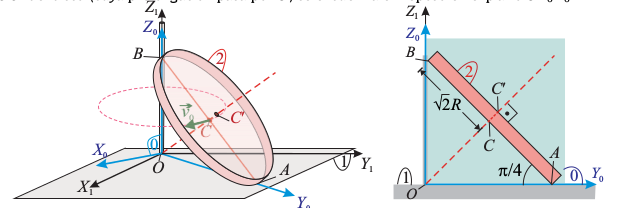
| | [[Imagen:F1_GIA_SPC_2013_disco_rotando_barra_vertical_enunciado.png|center]] | | [[Imagen:F1_GIA_SPC_2013_disco_rotando_barra_vertical_enunciado.png|center]] |
| - | Un disco de radio <math>\sqrt{2}R </math> y espesor no despreciable (sólido "2") se mueve respecto de un plano fijo <math>\Pi_1\equiv OX_1Y_1 </math> (sólido "1"). En cada instante, un punto del perímetro de la base inferior del disco está en contacto con el plano <math>\Pi_1 </math>, mientras que el diametralmente opuesto, se apoya sobre el eje fijo <math>OZ_1 </math>. En todo momento, las bases del disco forman un ángulo <math>\pi/4 </math> con el plano <math>\Pi_1 </math>. El movimiento del disco es tal que rueda sin deslizar sobre dicho plano, en el punto de contacto <math>A </math>. Además, el centro <math>C </math> de la base
| |
| - | inferior realiza un movimiento circular de radio <math>R </math> en torno al eje <math>OZ_1 </math>, en sentido horario y con velocidad de módulo constante <math>v_0 </math>. Para analizar el movimiento, se sugiere utilizar un sólido ("0") consistente en un sistema de referencia <math>OX_0Y_0Z_0 </math> tal que <math>OZ_0 = OZ_1 </math> en todo instante y que se mueve de manera que el eje <math>CC' </math> del disco (cuya prolongación pasa por <math>O </math>) se encuentra en reposo en el plano <math>OY_0Z_0 </math>.
| |
| - | #Trace los ejes de rotación de los movimientos {01}, {20} y {21} en el instante representado e identifique los tipos de movimiento.
| |
| - | #Encuentre la reducción cinemática y su derivada para el movimiento {21}.
| |
última version al 18:51 7 ene 2015
Masa subiendo por rampa
Satélite girando alrededor de la Tierra
Disco rotando alrededor de barra vertical