Entrar Página Discusión Historial Go to the site toolbox

Cuatro procesos no cuasiestáticos

De Laplace

(Diferencias entre revisiones)
Línea 46: Línea 46:
<center><math>p_E=100\,\mathrm{kPa}\qquad\qquad T_E=296\,\mathrm{K}\qquad\qquad V_E=4000\,\mathrm{cm}^3</math></center>
<center><math>p_E=100\,\mathrm{kPa}\qquad\qquad T_E=296\,\mathrm{K}\qquad\qquad V_E=4000\,\mathrm{cm}^3</math></center>
 +
 +
Quedan los estados B y D. Para ellos, debemos analizar los procesos.
 +
 +
Al estado B se llega cuando se retira el tope y de deja que el gas se expanda, sin quitar el aislante térmico. Esto quiere decir que en B hay equilibrio mecánico con el ambiente, pero no térmico. Por ello,
 +
 +
<center><math>p_B = 100\,\mathrm{kPa}</math></center>
 +
 +
No sabemos la temperatura ni el volumen en este estado. Sí sabemos que el proceso A&rarr;B es adiabático, por lo que se cumple la igualdad
 +
 +
<center><math>W +\overbrace{Q}^{=0}=\Delta U</math></center>
 +
 +
El proceso es adiabático, pero no cuasiestático. Por ello, no podemos emplear la ley de Poisson para hallar el nuevo estado. En su lugar, como en el problema de la [[Trabajo_en_una_compresión_por_un_peso#Caso_adiab.C3.A1tico|pesa]] y el del [[Masa_que_cuelga_de_una_cámara_de_aire#Caso_adiab.C3.A1tico|saco]] debemos calcular el trabajo teniendo en cuenta que la presión exterior es constante
 +
 +
<center><math>W=-\int_A^B p_\mathrm{ext}\,\mathrm{d}V=-p_\mathrm{ext}\,\Delta V</math></center>
 +
 +
o, en términos de las variables del sistema,
 +
 +
<center><math>W=-p_B(V_B-V_A)\,</math></center>
 +
 +
Igualando esto a la variación de la energía interna
 +
 +
<center><math>\Delta U = nc_v(T_B-T_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}</math></center>
 +
 +
queda la ecuación
 +
 +
<center><math>-p_B(V_B-V_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}</math></center>
 +
 +
cuya solución, como en los dos problemas mencionados, vale
 +
 +
<center><math>V_B = \left(1-\frac{p_B-p_A}{\gamma p_B}\right)V_A</math></center>
 +
 +
cuyo valro numérico es
 +
 +
<center><math>V_B = \left(1-\frac{100-450}{1.4\times 100}\right)\times 1000\,\mathrm{cm}^3 = 3500\,\mathrm{cm}^3</math></center>
 +
 +
Una vez que tenemos el volumen, hallamos la nueva temperatura mediante la ley de los gases ideales
 +
 +
<center><math>T_B=\frac{p_BV_B}{p_AV_A}T_A=259\,\mathrm{K}</math></center>
 +
 +
Vemos que la temperatura cae por debajo de la del ambiente. No hay problema en ello, pues el aislante térmico provoca que no haya equilibrio. Este es un caso de enfriamento adiabático: la expansión brusca de un gas hace bajar su temperatura.
 +
 +
Por último, queda el estado D. En este se retira el aislante térmico dejando el tope puesto. Por tanto su volumen es el mismo que el inicial
 +
 +
<center><math>V_D = V_A=1000\,\mathrm{cm}^3</math></center>
 +
 +
pero su temperatura se iguala a la del ambiente
 +
 +
<center><math>T_D=T_C=296\,\mathrm{K}</math></center>
 +
 +
Con la ley de los gases ideales obtenemos la presión en este estado
 +
 +
<center><math>p_D=\frac{T_D V_A}{T_A V_D}p_A=400\,\mathrm{kPa}</math></center>
 +
 +
Con esto ya tenemos la tabla completa de todos los estados:
 +
 +
{| class="bordeado"
 +
|-
 +
! Estado
 +
! p (kPa)
 +
! V (cm&sup3;)
 +
! T (K)
 +
|-
 +
! A
 +
| 450
 +
| 1000
 +
| 333
 +
|-
 +
! B
 +
| 100
 +
| 3500
 +
| 259
 +
|-
 +
! C
 +
| 100
 +
| 4000
 +
| 296
 +
|-
 +
! D
 +
| 400
 +
| 1000
 +
| 296
 +
|-
 +
! E
 +
| 100
 +
| 4000
 +
| 296
 +
|}

Revisión de 19:26 8 abr 2014

1 Enunciado

Se tiene un cilindro horizontal cerrado por un pistón, en cuyo interior hay aire seco (considerado un gas ideal diatómico). Inicialmente, el aire interior se encuentra a 450 kPa y 333 K, ocupando un volumen de 1000 cm³. El ambiente se encuentra a 100 kPa y 296 K, valores que no cambian en ningún momento.

Las paredes del cilindro son adiabáticas. El pistón está inicialmente limitado por un tope y forrado de forma que está aislado térmicamente.

Se realiza entonces el siguiente proceso compuesto:

  • A→B Se libera bruscamente el tope, dejando que el gas se expanda sin quitarle el aislante térmico.
  • B→C Una vez que se ha alcanzado de nuevo el equilibrio y sin volver a fijar la tapa, se quita bruscamente el aislante térmico, dejando que el sistema evolucione.

Ninguno de los dos pasos es cuasiestático.

Para este proceso

a.1 Calcule la presión, volumen y temperatura del gas en los estados B y C.
a.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→B y B→C.
a.3 Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos.

Suponga ahora que, partiendo del mismo estado inicial se realizan los dos desbloqueos en orden inverso, es decir,

  • A→D Se quita bruscamente el aislante térmico, sin quitar el tope
  • D→E Sin volver a poner el aislante, se libera bruscamente el tope.

Ninguno de los dos pasos es cuasiestático.

Para este nuevo proceso, calcule las mismas magnitudes que en el caso anterior, es decir:

b.1 Calcule la presión, volumen y temperatura del gas en los estados D y E.
b.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→D y D→E.
b.3 Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos.

2 Presiones, volúmenes y temperaturas

Comenzamos anotando los datos que conocemos e iremos rellenando los que podamos deducir de estos empleando la ley de los gases ideales y el conocimiento de los diferentes procesos.

Del estado inicial A tenemos toda la información

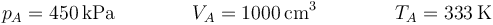
p_A=450\,\mathrm{kPa}\qquad\qquad V_A=1000\,\mathrm{cm}^3\qquad\qquad T_A=333\,\mathrm{K}

En el estado final C, el gas tiene la temperatura y la presión del ambiente, ya que ha alcanzado el equilibrio térmico y mecánico.

p_C=100\,\mathrm{kPa}\qquad\qquad T_C=296\,\mathrm{K}

Mediante la ley de los gases ideales calculamos el volumen en el estado final C

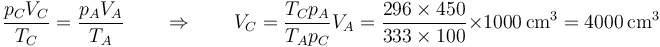
\frac{p_CV_C}{T_C}=\frac{p_AV_A}{T_A}\qquad\Rightarrow\qquad V_C=\frac{T_Cp_A}{T_Ap_C}V_A=\frac{296\times 450}{333\times 100}\times 1000\,\mathrm{cm}^3=4000\,\mathrm{cm}^3

El estado E es exactamente el mismo que el C: de equilibrio mecánico y térmico con el ambiente. Por ello:

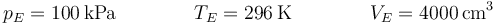
p_E=100\,\mathrm{kPa}\qquad\qquad T_E=296\,\mathrm{K}\qquad\qquad V_E=4000\,\mathrm{cm}^3

Quedan los estados B y D. Para ellos, debemos analizar los procesos.

Al estado B se llega cuando se retira el tope y de deja que el gas se expanda, sin quitar el aislante térmico. Esto quiere decir que en B hay equilibrio mecánico con el ambiente, pero no térmico. Por ello,

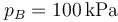
p_B = 100\,\mathrm{kPa}

No sabemos la temperatura ni el volumen en este estado. Sí sabemos que el proceso A→B es adiabático, por lo que se cumple la igualdad

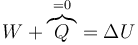
W +\overbrace{Q}^{=0}=\Delta U

El proceso es adiabático, pero no cuasiestático. Por ello, no podemos emplear la ley de Poisson para hallar el nuevo estado. En su lugar, como en el problema de la pesa y el del saco debemos calcular el trabajo teniendo en cuenta que la presión exterior es constante

W=-\int_A^B p_\mathrm{ext}\,\mathrm{d}V=-p_\mathrm{ext}\,\Delta V

o, en términos de las variables del sistema,

W=-p_B(V_B-V_A)\,

Igualando esto a la variación de la energía interna

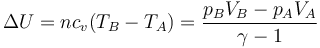
\Delta U = nc_v(T_B-T_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}

queda la ecuación

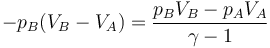
-p_B(V_B-V_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}

cuya solución, como en los dos problemas mencionados, vale

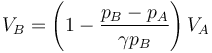
V_B = \left(1-\frac{p_B-p_A}{\gamma p_B}\right)V_A

cuyo valro numérico es

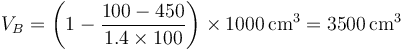
V_B = \left(1-\frac{100-450}{1.4\times 100}\right)\times 1000\,\mathrm{cm}^3 = 3500\,\mathrm{cm}^3

Una vez que tenemos el volumen, hallamos la nueva temperatura mediante la ley de los gases ideales

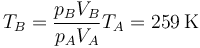
T_B=\frac{p_BV_B}{p_AV_A}T_A=259\,\mathrm{K}

Vemos que la temperatura cae por debajo de la del ambiente. No hay problema en ello, pues el aislante térmico provoca que no haya equilibrio. Este es un caso de enfriamento adiabático: la expansión brusca de un gas hace bajar su temperatura.

Por último, queda el estado D. En este se retira el aislante térmico dejando el tope puesto. Por tanto su volumen es el mismo que el inicial

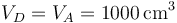
V_D = V_A=1000\,\mathrm{cm}^3

pero su temperatura se iguala a la del ambiente

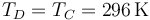
T_D=T_C=296\,\mathrm{K}

Con la ley de los gases ideales obtenemos la presión en este estado

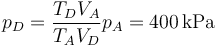
p_D=\frac{T_D V_A}{T_A V_D}p_A=400\,\mathrm{kPa}

Con esto ya tenemos la tabla completa de todos los estados:

Estado p (kPa) V (cm³) T (K)
A 450 1000 333
B 100 3500 259
C 100 4000 296
D 400 1000 296
E 100 4000 296
Obtenido de "http://tesla.us.es/wiki/index.php/Cuatro_procesos_no_cuasiest%C3%A1ticos"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace