Tercera convocatoria 2012/13 (F2GIA)
De Laplace
(Diferencias entre revisiones)
(→Esfera rellena de dos distribuciones de carga) |
|||
| Línea 1: | Línea 1: | ||
| + | ==[[Obtención_de_las_capacidades_caloríficas_de_un_gas,_F2_GIA_(Nov,_2012)|Obtención de las capacidades caloríficas de un gas]]== | ||
| + | En el interior de un recipiente, cerrado mediante un pistón móvil, hay <math>4.48</math> litros de un gas ideal que inicialmente se encuentra a la presión de <math>1\,\mathrm{atm}</math> y <math>0{}^\mathrm{o}\,\mathrm{C}</math> de temperatura. Las paredes del recipiente y el pistón pueden considerarse perfectamente impermeables al calor. Para determinar las características del gas se desplaza el pistón | ||
| + | de manera cuasiestática, comprimiendo aquél hasta que su volumen se reduce a la mitad del inicial. Se mide la presión y se comprueba que ésta es ahora <math>2.64\,\mathrm{atm}.</math> | ||
| + | |||
| + | # ¿Cuál es el valor del coeficiente adiabático del gas? ¿Puede decir si se trata de un gas monoatómico o diatómico? | ||
| + | # Determine los valores de las capacidades caloríficas y los calores específicos molares del gas. | ||
| + | |||
| + | '''Dato''': <math>R=0.082\,\mathrm{atm\, l}/(\mathrm{mol\, K})=8.314\,\mathrm{J}/(\mathrm{mol\, K})</math> | ||
| + | |||
| + | |||
==[[Esfera rellena de carga,_F2_GIA_(Nov,_2012)|Esfera rellena de dos distribuciones de carga]]== | ==[[Esfera rellena de carga,_F2_GIA_(Nov,_2012)|Esfera rellena de dos distribuciones de carga]]== | ||
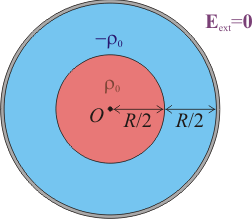
Una esfera metálica hueca de radio <math>R</math>, espesor despreciable y centro en el punto <math>O</math>, está rellena con dos distribuciones de carga eléctrica concéntricas con la esfera. La interior es de carga positiva y se distribuye uniformemente en la región esférica que se extiende desde el centro <math>O</math> hasta una distancia <math>r = R/2</math>, siendo la densidad de carga <math>\rho_0</math>. Una membrana (descargada), separa esta carga positiva de otra distribución uniforme de carga negativa, de densidad <math>−\rho_0</math>, que se extiende desde <math>r = R/2</math> hasta la superficie interior del hueco.[[Archivo:esfera_rellena_carga_0.gif|right]] | Una esfera metálica hueca de radio <math>R</math>, espesor despreciable y centro en el punto <math>O</math>, está rellena con dos distribuciones de carga eléctrica concéntricas con la esfera. La interior es de carga positiva y se distribuye uniformemente en la región esférica que se extiende desde el centro <math>O</math> hasta una distancia <math>r = R/2</math>, siendo la densidad de carga <math>\rho_0</math>. Una membrana (descargada), separa esta carga positiva de otra distribución uniforme de carga negativa, de densidad <math>−\rho_0</math>, que se extiende desde <math>r = R/2</math> hasta la superficie interior del hueco.[[Archivo:esfera_rellena_carga_0.gif|right]] | ||
Revisión de 12:54 16 jun 2013
1 Obtención de las capacidades caloríficas de un gas
En el interior de un recipiente, cerrado mediante un pistón móvil, hay 4.48 litros de un gas ideal que inicialmente se encuentra a la presión de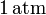 
y 
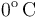de temperatura. Las paredes del recipiente y el pistón pueden considerarse perfectamente impermeables al calor. Para determinar las características del gas se desplaza el pistón
de manera cuasiestática, comprimiendo aquél hasta que su volumen se reduce a la mitad del inicial. Se mide la presión y se comprueba que ésta es ahora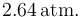 
- ¿Cuál es el valor del coeficiente adiabático del gas? ¿Puede decir si se trata de un gas monoatómico o diatómico?
- Determine los valores de las capacidades caloríficas y los calores específicos molares del gas.
Dato: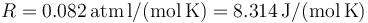 
2 Esfera rellena de dos distribuciones de carga
Una esfera metálica hueca de radio R, espesor despreciable y centro en el punto O, está rellena con dos distribuciones de carga eléctrica concéntricas con la esfera. La interior es de carga positiva y se distribuye uniformemente en la región esférica que se extiende desde el centro O hasta una distancia r = R / 2, siendo la densidad de carga ρ0. Una membrana (descargada), separa esta carga positiva de otra distribución uniforme de carga negativa, de densidad ρ0, que se extiende desde r = R / 2 hasta la superficie interior del hueco.
- Determine la carga eléctrica de cada una de las distribuciones volumétricas del interior de la esfera.
- Aplicando la ley de Gauss para el campo eléctrico, determine la cantidad total de carga eléctrica en la corteza esférica conductora para que el campo eléctrico en el exterior (para
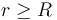) sea nulo en todos los puntos.
- En las condiciones del apartado anterior, obtenga la expresión del campo eléctrico en todos los puntos del espacio.
- ¿Qué valor tiene el potencial electrostático en la corteza conductora si el campo eléctrico es nulo en el exterior? Calcule el valor del potencial electrostático en los puntos de la membrana que separa las dos distribuciones volumétricas de carga.
