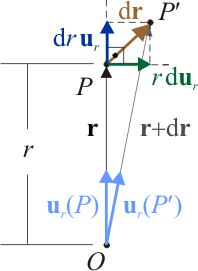Esfera rellena de carga, F2 GIA (Nov, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

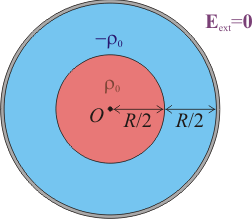
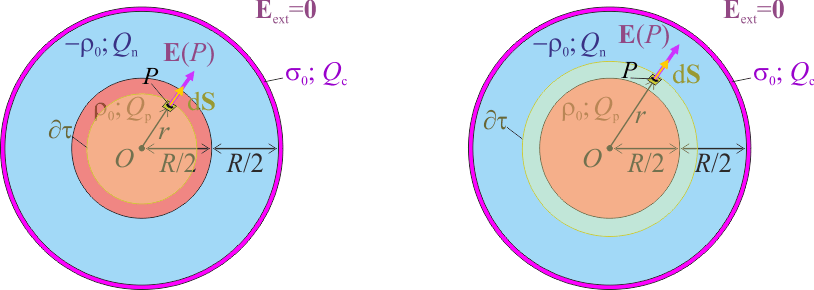
Una esfera metálica hueca de radio

R

, espesor despreciable y centro en el punto

O

, está rellena con dos distribuciones de carga eléctrica concéntricas con la esfera. La interior es de carga positiva y se distribuye uniformemente en la región esférica que se extiende desde el centro

O

hasta una distancia

r = R / 2

, siendo la densidad de carga

ρ 0

. Una membrana (descargada), separa esta carga positiva de otra distribución uniforme de carga negativa, de densidad

ρ 0

, que se extiende desde

r = R / 2

hasta la superficie interior del hueco.

Determine la carga eléctrica de cada una de las distribuciones volumétricas del interior de la esfera.
Aplicando la ley de Gauss para el campo eléctrico, determine la cantidad total de carga eléctrica en la corteza esférica conductora para que el campo eléctrico en el exterior (para 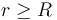$r \geq R$ ) sea nulo en todos los puntos.
En las condiciones del apartado anterior, obtenga la expresión del campo eléctrico en todos los puntos del espacio.
¿Qué valor tiene el potencial electrostático en la corteza conductora si el campo eléctrico es nulo en el exterior? Calcule el valor del potencial electrostático en los puntos de la membrana que separa las dos distribuciones volumétricas de carga.

2 Solución

2.1 Carga eléctrica en cada distribución volumétrica

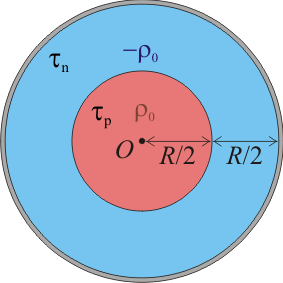
La región

τ p

, ocupada por la distribución de carga positiva, es un volumén esférico de radio

R / 2

. Como dicha carga se distribuye uniformemente, la cantidad de carga por unidad de volumen en cada punto de

τ p

tiene el mismo valor

ρ

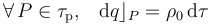
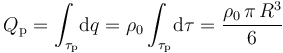
. La cantidad total de carga será igual a este valor de densidad multiplicado por el volumen: $\forall\, P\in\tau_\mathrm{p}\mathrm{,}\quad \mathrm{d}q\rfloor_P=\rho_0\!\ \mathrm{d}\tau$ $\Rightarrow$ $Q_\mathrm{p}=\int_{\tau_\mathrm{p}}\!\mathrm{d}q=\rho_0\int_{\tau_\mathrm{p}}\!\mathrm{d}\tau=\frac{\rho_0\!\ \pi\!\ R^3}{6}$

La región $τ n$ de carga negativa es la corona comprendida entre las superficies esféricas concéntricas de radios $R / 2$ y $R$ . Esta distribución de carga es también uniforme, de manera que la densidad volumétrica tendrá el mismo valor $- ρ 0$ en todos los puntos de $τ n$ . Se tendrá, por tanto,

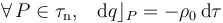
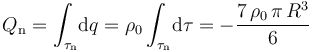
$\forall\, P\in\tau_\mathrm{n}\mathrm{,}\quad \mathrm{d}q\rfloor_P=-\rho_0\!\ \mathrm{d}\tau$ $\Rightarrow$ $Q_\mathrm{n}=\int_{\tau_\mathrm{n}}\!\mathrm{d}q=\rho_0\int_{\tau_\mathrm{n}}\!\mathrm{d}\tau=-\frac{7\!\ \rho_0\!\ \pi\!\ R^3}{6}$

2.2 Carga eléctrica en la corteza conductora

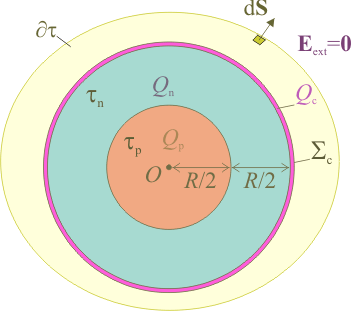
La ley de Gauss establece que el flujo del campo eléctrico a través de una superficie cerrada $\partial\tau$ es proporcional a la cantidad total de carga eléctrica que hay dentro del volumen $τ$ . Si tomamos una superficie gaussiana cerrada $\partial\tau$ que incluya en su volumen a la esfera metálica cargada, el flujo del campo eléctrico a través de aquélla deberá ser proporcional a la suma de las cargas $Q p$ , $Q n$ , y la $Q c$ que hubiera distribuida superficialmente en la corteza de la esfera, de espesor despreciable. Y, por otra parte, se nos indica que el campo eléctrico es nulo en el exterior de la esfera y, en particular, en los puntos de dicha superficie $\partial\tau$ . Esta información nos permite determinar la cantidad total de carga eléctrica $Q c$ que se distribuye en la corteza esférica conductora, ya que el flujo total del campo eléctrico a través de dicha superficie debe ser nulo:

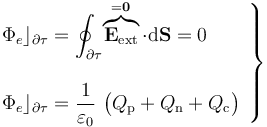
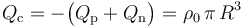
$\left.\begin{array}{l}\displaystyle\Phi_e\rfloor_{\partial\tau}=\oint_{\partial\tau}\!\overbrace{\mathbf{E}_\mathrm{ext}}^{=\mathbf{0}}\cdot\mathrm{d}\mathbf{S}=0\\ \\ \displaystyle\Phi_e\rfloor_{\partial\tau}=\frac{1}{\varepsilon_0}\ \big(Q_\mathrm{p}+Q_\mathrm{n}+Q_\mathrm{c}\big) \end{array}\right\}$ $\quad$ $\Rightarrow$ $Q_\mathrm{c}=-\big(Q_\mathrm{p}+Q_\mathrm{n}\big)=\rho_0\!\ \pi\!\ R^3$

Y dado que el resto de las cargas del sistema (las distribuciones volumétricas del interior de esfera) se distribuyen uniformemente, con simetría esférica, la carga que hay en la superficie esférica conductora $Σ c$ , también se distribuirá según una densidad superficial constante:

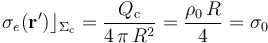
$\sigma_e(\mathbf{r}^\prime)\rfloor_{\Sigma_\mathrm{c}}=\frac{Q_\mathrm{c}}{4\!\ \pi\!\ R^2}=\frac{\rho_0\!\ R}{4}=\sigma_0$

2.3 Expresión del campo eléctrico en todos los puntos del espacio

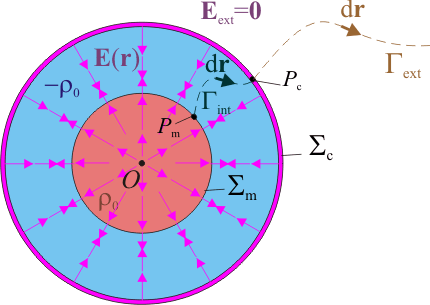
Como hemos visto, todas las distribuciones de carga presentes en el sistema son uniformes y tienen simetría esférica. En el siguiente enlace puede encontrarse la justificación de que el campo eléctrico creado por una distribución superficial en un corteza esférica, produce un campo con simetría radial respecto del centro de la esfera. El mismo razonamiento puede emplearse para las distribuciones volumétricas en $τ p$ y $τ n$ , obteniéndose idéntico resultado. Y como la tres distribuciones son concéntricas en el punto $O$ , y producen sendos campos radiales con centro en $O$ , el campo 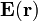$\mathbf{E}(\mathbf{r})$ resultante de la superposición será también radial con centro en dicho punto. Por otra parte, hemos calculado que cantidad de carga deber hacer en la corteza de radio para que el campo en el exterior sea nulo. Por tanto, sólo en el interior existirá un campo eléctrico que en cada punto $P$ es colineal con el vector 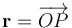$\mathbf{r}=\overrightarrow{OP}$ , y cuya intensidad sólo depende de la distancia 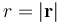$r=|\mathbf{r}|$ al centro $O$ de la distribución:

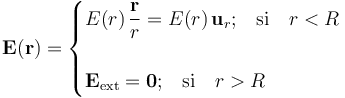
$\mathbf{E}(\mathbf{r})=\begin{cases}\displaystyle E(r)\!\ \frac{\mathbf{r}}{r}=E(r)\!\ \mathbf{u}_r\mathrm{;} \quad \mathrm{si}\quad r<R\\ \\ \mathbf{E}_\mathrm{ext}=\mathbf{0}\mathrm{;} \quad \mathrm{si}\quad r>R\end{cases}$

Para determinar el valor de la función $E (r)$ aplicamos la ley de Gauss en superficies gaussinas esféricas $\partial \tau$ con centro en $O$ y radio $r < R$ . En cada punto $P$ de estas gaussianas, el vector elemento de superficie es también colineal con el correspondiente vector $\mathbf{r}$ . Se tendrá, por tanto:

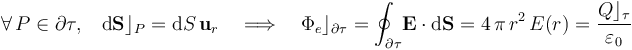
$\forall\, P\in\partial\tau\mathrm{,}\quad\mathrm{d}\mathbf{S}\rfloor_P=\mathrm{d}S\!\ \mathbf{u}_r\quad\Longrightarrow\quad\Phi_e\rfloor_{\partial\tau}=\oint_{\partial\tau}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=4\!\ \pi\!\ r^2\!\ E(r)=\frac{Q\rfloor_\tau}{\varepsilon_0}$

La cantidad de carga contenida en el interior de $τ$ depende del radio de la superficie esférica $\partial \tau$ . Si $r < R / 2$ , el volumen $τ$ contendrá la fracción de la carga $Q p$ correspondiente a dicho volumen esférico de radio $r$ . Si $R / 2 < r < R$ , en el interior de $τ$ se tendrá toda la carga $Q p$ más la fracción de $Q n$ contenida en la corona esférica comprendida entre los radios de valor $R / 2$ y $r$ :

$Q\rfloor_\tau=Q(r)\begin{cases}\displaystyle \frac{4}{3}\!\ \pi\!\ \rho_0\!\ r^3\mathrm{;}\quad\mathrm{si}\quad 0\leq r\leq R/2\\ \\ \displaystyle Q_\mathrm{p}-\frac{4}{3}\!\ \pi\!\ \rho_0\!\ \bigg[r^3-\bigg(\frac{R}{2}\bigg)^3\bigg]=\frac{1}{3}\!\ \pi\!\ \rho_0\!\ R^3\!\ \bigg[1-4\!\ \bigg(\frac{r}{R}\bigg)^3\bigg] \mathrm{;}\quad\mathrm{si}\quad R/2\leq r<R \end{cases}$

Y exigiendo que se verifique la ley de Gauss, se obtiene la expresión del campo eléctrico creado por la distribución de carga bajo estudio en cualquier punto del espacio:

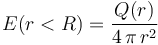
$E(r<R)=\frac{Q(r)}{4\!\ \pi\!\ r^2}$ $\Rightarrow$ $\mathbf{E}(\mathbf{r})=\begin{cases}\displaystyle \frac{\rho_0}{3\!\ \varepsilon_0}\!\ \mathbf{r}\mathrm{;} \quad \mathrm{si}\quad 0\leq r\leq R/2\\ \\ \displaystyle -\frac{\rho_0}{3\!\ \varepsilon_0}\!\ \bigg[1-\frac{1}{4}\bigg(\frac{R}{r}\bigg)^3\bigg]\!\ \mathbf{r}\mathrm{;} \quad \mathrm{si}\quad R/2\leq r<R \\ \\ \mathbf{E}_\mathrm{ext}=\mathbf{0}\mathrm{;} \quad \mathrm{si}\quad r>R\end{cases}$

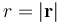donde $r=|\mathbf{r}|$ .

2.4 Potencial electrostático

Dado un campo eléctrico 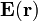$\mathbf{E}(\mathbf{r})$ creado por una distribución arbitraria de cargas, se define un campo escalar 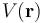$V(\mathbf{r})$ , llamado potencial electrostrático, tal que la diferencia entre los valores de dicho campo en dos del espacio es igual a la circulación del campo eléctrico entre esos puntos, siguiendo cualquier camino; concretamente,

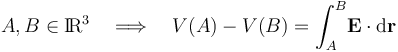
$A,B\in \mathrm{I}\!\mathrm{R}^3\quad\Longrightarrow\quad V(A)-V(B)=\int_A^B\!\mathbf{E}\cdot\mathrm{d}\mathbf{r}$

Esta propiedad general del potencial electrostático podemos utilizarla para calcular los valores del potencial en los puntos de la corteza conductora esféricadel sistema bajo estudio, así como en los puntos de la membrana que separa las distribuciones volumétricas de carga que hay en el interior de dicha corteza:

2.4.1 Potencial en la corteza esférica conductora

Sea $P c$ un punto arbitrario de la superficie esférica $Σ c$ de radio $R$ . La diferencia entre el valor del potencial en este punto y en otro situado en el infinito será igual a la circulación del campo entre ambos puntos, a la largo de cualquier trayectoria. Tomemos una trayectoria $Γ ext$ tal que todos sus puntos sean exteriores a la esfera. Según se indicia en el enunciado, la distribución de cargas es tal que en todos estos puntos “exteriores” el campo eléctrico es nulo. En consecuencia, la circulación desde cualquier punto de la superficie $Σ c$ hasta cualquier punto del infinito será también nula:

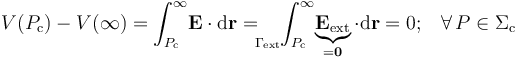
$V(P_\mathrm{c})-V(\infty)=\int_{P_\mathrm{c}}^\infty\!\mathbf{E}\cdot\mathrm{d}\mathbf{r}=\;\;\;\int_{P_\mathrm{c}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\Gamma_\mathrm{ext}}^\infty\!\underbrace{\mathbf{E}_\mathrm{ext}}_{=\mathbf{0}}\cdot\mathrm{d}\mathbf{r}=0\mathrm{;}\quad\forall\, P\in\Sigma_\mathrm{c}$

En conscuencia, todos los puntos de la superficie esférica $Σ c$ se encuentran al mismo potencial que los puntos del infinito. Pero éste hemos de entenderlo como la región del espacio formada por todos aquellos puntos lo suficientemente alejados de nuestro sistema de cargas como para que éste no produzca perturbaciones apreciables. Es decir, en el infinito, tanto los campos eléctricos como los potenciales electrostáticos creados por las distribuciones de carga que hay en la superficie y el interior de la esfera son nulos. Por tanto,

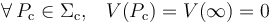
$\forall\, P_\mathrm{c}\in\Sigma_\mathrm{c}\mathrm{,}\quad V(P_\mathrm{c})=V(\infty)=0$

2.4.2 Potencial en la membrana de separación

La diferencia de potencial entre un punto $P m$ de la membrana de separación y otro $P c$ de la superficie esférica conductora es igual a la circulación del campo eléctrico desde el primero hasta el segundo:

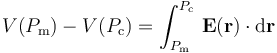
$V(P_\mathrm{m})-V(P_\mathrm{c})=\int_{P_\mathrm{m}}^{P_\mathrm{c}}\!\ \mathbf{E}(\mathbf{r})\cdot\mathrm{d}\mathbf{r}$

Como ya sabemos, el valor de esta circulación es independiente del camino seguido para calcularla, ya que el dicho campo eléctrico es debido a distribuciones de cargas estáticas. Así que consideraremos un camino que vaya de un punto arbitrario $P m$ de la membrana hasta otro $P c$ de la corteza, recorriendo la región comprendida entre ambas superficies. Así que el integrando hemos de calcularlo a partir de la expresión del campo eléctrico para dicha región:

$\mathbf{E}(\mathbf{r})\cdot\mathrm{d}\mathbf{r}=-\frac{\rho_0}{3\!\ \varepsilon_0}\!\ \bigg[1-\frac{1}{4}\bigg(\frac{R}{r}\bigg)^3\bigg]\!\ \mathbf{r}\cdot\mathrm{d}\mathbf{r}$

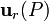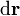Expresemos el radio-vector posición en términos de su módulo $r$ , y de un vector unitario $\mathbf{u}_r(P)$ con la dirección y sentido del segmento orientado $\overrightarrow{OP}$ . El vector infinitesimal $\mathrm{d}\mathbf{r}$ entre dos puntos infinitamente próximos puede expresarse como la suma de sus proyecciones en la dirección de 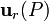$\mathbf{u}_r(P)$ , y en otra ortogonal a ésta:

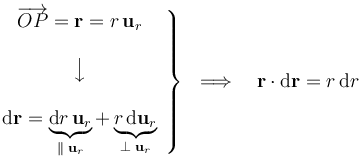
$\left.\begin{array}{c}\displaystyle\overrightarrow{OP}=\mathbf{r}=r\!\ \mathbf{u}_r\\ \\ \big\downarrow\\ \\ \displaystyle\mathrm{d}\mathbf{r}=\underbrace{\mathrm{d}r\!\ \mathbf{u}_r}_{\|\!\ \mathbf{u}_r}+\underbrace{r\!\ \mathrm{d}\mathbf{u}_r}_{\perp\!\ \mathbf{u}_r}\end{array}\right\}\;\;\Longrightarrow\quad \mathbf{r}\cdot\mathrm{d}\mathbf{r}=r\!\ \mathrm{d}r$

En consecuencia, la diferencia de potencial entre los puntos $P m$ y $P c$ la obtenemos integrando los elementos de circulación del campo eléctrico entre los valores $r = R / 2$ y $r = R$ . Teniendo en cuenta, además, que el potencial en la superficie conductora exterior es nulo, se obtiene el valor del potencial electrostático creado por la distribución de carga en cualquier punto $P m$ de la membrana que separa las dos distribuciones volumétricas:

$V(P_\mathrm{m})-V(P_\mathrm{c})=-\frac{\rho_0}{3\!\ \varepsilon_0}\!\ \int_{R/2}^{R}\!\bigg[1-\frac{1}{4}\bigg(\frac{R}{r}\bigg)^3\bigg]\!\ r\!\ \mathrm{d}r$ $\Rightarrow$ $V(P_\mathrm{m})=-\frac{\rho_0\!\ R^2}{24\!\ \varepsilon_0}$

Esfera rellena de carga, F2 GIA (Nov, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Carga eléctrica en cada distribución volumétrica

2.2 Carga eléctrica en la corteza conductora

2.3 Expresión del campo eléctrico en todos los puntos del espacio

2.4 Potencial electrostático

2.4.1 Potencial en la corteza esférica conductora

2.4.2 Potencial en la membrana de separación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES