Segunda convocatoria 2011/12 (F2GIA)
De Laplace
(Diferencias entre revisiones)
(→Barras conductoras en paralelo) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
'''Datos''': calor específico del agua, <math>c_a=1\,\mathrm{cal}/(\mathrm{g}\ \mathrm{K})</math>; calor específico del hielo, <math>c_h=0.5\,\mathrm{cal}/(\mathrm{g}\ \mathrm{K})</math>; calor latente de fusión del hielo, | '''Datos''': calor específico del agua, <math>c_a=1\,\mathrm{cal}/(\mathrm{g}\ \mathrm{K})</math>; calor específico del hielo, <math>c_h=0.5\,\mathrm{cal}/(\mathrm{g}\ \mathrm{K})</math>; calor latente de fusión del hielo, | ||
<math>L_{fh}=80\,\mathrm{cal}/\mathrm{g}</math>; calor latente de vaporización del agua, <math>L_{va}=540\,\mathrm{cal}/\mathrm{g}</math>. | <math>L_{fh}=80\,\mathrm{cal}/\mathrm{g}</math>; calor latente de vaporización del agua, <math>L_{va}=540\,\mathrm{cal}/\mathrm{g}</math>. | ||
| + | |||
| + | | ||
| + | |||
| + | ==[[Barras_conductoras_en_paralelo,_F2_GIA_(Sept,_2012)|Barras conductoras en paralelo]]== | ||
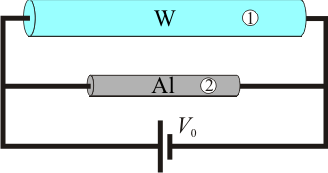
| + | [[Archivo:barras_paralelo_0.gif|right]]La longitud y el diámetro de una barra cilíndrica de wolframio o tungsteno (W) son el doble que los de otra barra de aluminio (Al). En ambos casos, la longitud de la barra es mucho mayor que su diámetro. Los extremos de ambas están conectados a los bornes o polos de una batería de fuerza electromotriz <math>V_0</math> y resistencia interna despreciable, constituyendo una asociación de resistencias ''en paralelo''. Sabiendo que la conductividad eléctrica del aluminio es prácticamente el doble que la del tungsteno, determine las relaciones entre las siguientes magnitudes: | ||
| + | |||
| + | # Resistencias eléctricas de las barras e intensidades de corriente. | ||
| + | # Densidad de corriente e intensidad del campo eléctrico en el interior de los conductores. | ||
==[[Sistema_de_tres_discos_conductores,_F2_GIA_(Sept,_2012)|Sistema de tres discos conductores]]== | ==[[Sistema_de_tres_discos_conductores,_F2_GIA_(Sept,_2012)|Sistema de tres discos conductores]]== | ||
última version al 12:25 15 abr 2013
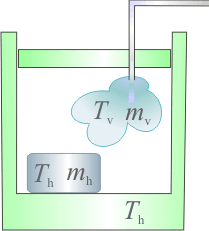
1 Estado final de mezcla de hielo y vapor
Un calorímetro, cuya capacidad calorífica (o equivalente en agua) es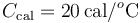 , se encuentra en equilibrio térmico con
, se encuentra en equilibrio térmico con 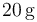 de hielo a
de hielo a 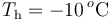 que contiene en su interior. Se introducen
que contiene en su interior. Se introducen 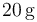 de vapor de agua a
de vapor de agua a 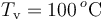 , provocando un desequilibrio en el sistema. Determine el estado final de la mezcla (temperatura y cantidades de agua líquida, hielo y vapor) cuando se recupera el equilibrio térmico, sabiendo que en todo momento se mantiene una presión de 1 atmósfera.
, provocando un desequilibrio en el sistema. Determine el estado final de la mezcla (temperatura y cantidades de agua líquida, hielo y vapor) cuando se recupera el equilibrio térmico, sabiendo que en todo momento se mantiene una presión de 1 atmósfera.
Datos: calor específico del agua, 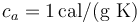 ; calor específico del hielo,
; calor específico del hielo, 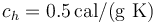 ; calor latente de fusión del hielo,
; calor latente de fusión del hielo,
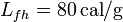 ; calor latente de vaporización del agua,
; calor latente de vaporización del agua, 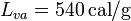 .
.
2 Barras conductoras en paralelo
La longitud y el diámetro de una barra cilíndrica de wolframio o tungsteno (W) son el doble que los de otra barra de aluminio (Al). En ambos casos, la longitud de la barra es mucho mayor que su diámetro. Los extremos de ambas están conectados a los bornes o polos de una batería de fuerza electromotriz V0 y resistencia interna despreciable, constituyendo una asociación de resistencias en paralelo. Sabiendo que la conductividad eléctrica del aluminio es prácticamente el doble que la del tungsteno, determine las relaciones entre las siguientes magnitudes:- Resistencias eléctricas de las barras e intensidades de corriente.
- Densidad de corriente e intensidad del campo eléctrico en el interior de los conductores.
3 Sistema de tres discos conductores
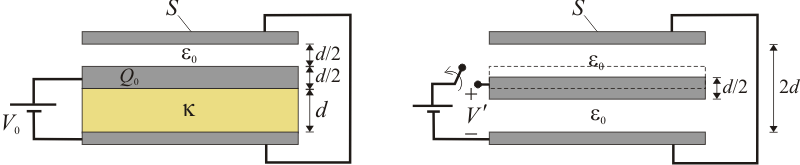
Se tiene un sistema formado por tres discos conductores de igual sección S, con sus superficies planas dispuestas en planos paralelos. El disco intermedio tiene un espesor d / 2 y está separado del disco inferior por una lámina de metacrilato de espesor d, cuya constante dieléctrica tiene un valor 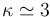 ; una capa de aire de espesor d / 2 lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde.
; una capa de aire de espesor d / 2 lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde.
- Determine las capacidades eléctricas de los dos condensadores formados por las superficies planas enfrentadas, en términos de los parámetros del sistema.
- Si se conectan los dos discos externos mediante un hilo conductor, ¿qué tipo de asociación de condensadores se forma? ¿Cuánto vale la capacidad eléctrica equivalente?
- En la situación del apartado anterior, determine la cantidad total de carga eléctrica en el conductor central cuando entre éste y los externos se establece una diferencia de potencial V0 mediante un generador electrostático. Determine también las cantidades de carga eléctrica en cada una de las superficies planas de los conductores.
- Tras desconectar el generador, dejando los discos aislados, se quita la lámina dieléctrica y, posteriormente, se desplaza el disco central de manera que sus superficies planas equidisten de los discos externos ¿Cúal será el valor
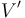 de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema.
de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema.
- Sabiendo que los campos máximos de ruptura dieléctrica del aire y del metacrilato son de
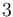 y
y 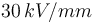 , respectivamente, y considerando que
, respectivamente, y considerando que 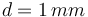 , determine cuál es el valor máximo que puede tener V0 para que en ningún momento se produzca la ruptura dieléctrica.
, determine cuál es el valor máximo que puede tener V0 para que en ningún momento se produzca la ruptura dieléctrica.