Tercera Convocatoria Ordinaria 2012/13 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(Página creada con 'Categoría: Problemas de examen == Tiro parabólico sobre un plano inclinado== [[Imagen:F1_GIC_tiro_pa…') |
|||
| Línea 8: | Línea 8: | ||
#Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante. | #Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante. | ||
#Para el caso <math>\alpha=\pi/3</math>, calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura. | #Para el caso <math>\alpha=\pi/3</math>, calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura. | ||
| + | |||
| + | ==[[Barra apoyada sobre una pared inclinada, Diciembre 2012 (G.I.C.)| Barra apoyada sobre una pared inclinada]]== | ||
| + | [[Imagen:F1_GIC_barra_sobre_pared_inclinada_enunciado.png|right]] | ||
| + | La barra de la figura forma un ángulo <math>\alpha</math> con la horizontal y está apoyada | ||
| + | sobre una pared inclinada <math>\pi/4</math>. El peso de la barra está aplicado en su | ||
| + | centro. El contacto en el punto <math>A</math> es liso, mientras que en el punto <math>B</math> es | ||
| + | rugoso con un coeficiente de rozamiento estático <math>\mu</math>. | ||
| + | #Dibuja el diagrama de sólido libre de la barra. | ||
| + | #Considerando el ángulo <math>\alpha</math> como un dato, calcula las fuerzas sobre la barra en los puntos <math>A</math> y <math>B</math>. | ||
| + | #¿Para que valores del ángulo <math>\alpha</math> es posible el equilibrio? | ||
última version al 14:19 16 ene 2013
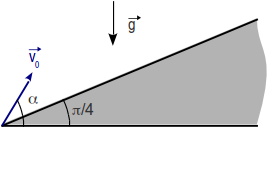
1 Tiro parabólico sobre un plano inclinado
Se tiene el plano inclinado de la figura que forma un ángulo π / 4 con la horizontal.
se dispara una partícula desde el punto más bajo, con una velocidad inicial
 , de módulo v0 y con un ángulo α con la horizontal.
, de módulo v0 y con un ángulo α con la horizontal.
- Calcula la distancia entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
- Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante.
- Para el caso α = π / 3, calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura.
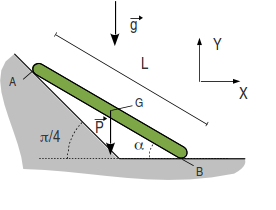
2 Barra apoyada sobre una pared inclinada
La barra de la figura forma un ángulo α con la horizontal y está apoyada sobre una pared inclinada π / 4. El peso de la barra está aplicado en su centro. El contacto en el punto A es liso, mientras que en el punto B es rugoso con un coeficiente de rozamiento estático μ.
- Dibuja el diagrama de sólido libre de la barra.
- Considerando el ángulo α como un dato, calcula las fuerzas sobre la barra en los puntos A y B.
- ¿Para que valores del ángulo α es posible el equilibrio?