Oscilaciones amortiguadas (GIE)
De Laplace
(→Ecuación del oscilador amortiguado) |
(→Solución de la ecuación) |
||
| Línea 101: | Línea 101: | ||
==Solución de la ecuación== | ==Solución de la ecuación== | ||
| + | ===Caracterización de las soluciones=== | ||
| + | Antes de examinar la solución matemática de la ecuación diferencial, podemos describir como deberían ser las soluciones. | ||
| + | |||
| + | * Si el rozamiento es pequeño, debemos esperar que el resorte oscile paro con una amplitud decreciente, hasta que pasado un cierto tiempo se quede en reposo en la posición de equilibrio. | ||
| + | |||
| + | * Si el rozamiento es muy grande, en cambio, debemos esperar que no llegue a oscile, sino que simplemente se vaya moviendo lentamente hasta la posición de equilibrio. | ||
| + | |||
| + | En física siempre que una magnitud se considera grande o pequeña hay que decir comparada con qué, cuál es el patrón en que nos basamos para decir si algo es grande o pequeño. En este caso aprovechamos que tanto <math>\beta</math> como <math>\omega_0</math> tienen las mismas dimensiones y por tanto se pueden comparar. Establecemos entonces el criterio | ||
| + | |||
| + | * Rozamiento débil: <math>\beta < \omega_0</math> | ||
| + | * Rozamiento intenso: <math>\beta > \omega_0</math> | ||
| + | |||
| + | La solución matemática debe reflejar por tanto un cambio de comportamiento dependiendo de como sea la constante de amortiguamiento comparada con la frecuencia propia. | ||
| + | |||
| + | ===Solución matemática=== | ||
| + | |||
==Caso sobreamortiguado== | ==Caso sobreamortiguado== | ||
==Caso subamortiguado== | ==Caso subamortiguado== | ||
Revisión de 13:39 6 dic 2012
Contenido |
1 El oscilador no amortiguado
En otras secciones se estudia la cinemática y la dinámica del oscilador armónico. Éste es un sistema ideal gobernado por la ley de Hooke. Típicamente esta ley se aplica a resortes mecánicos, aunque puede generalizarse a muchas otras situaciones. En el caso de un resorte que oscila en una sola dimensión la ley de Hooke se escribe
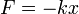
siendo x la elongación del resorte (distancia respecto a la posición de equilibrio)
Una partícula sometida exclusivamente a la ley de Hooke en una dimensión cumple la ecuación de movimiento

Este es un caso particular de la ecuación para un movimiento armónico simple
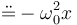
siendo en este caso la frecuencia natural
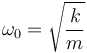
La solución general de esta ecuación diferencial es una oscilación sinusoidal
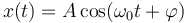
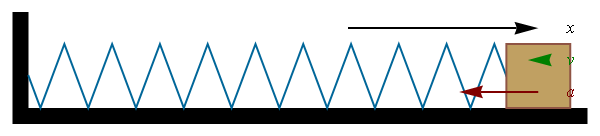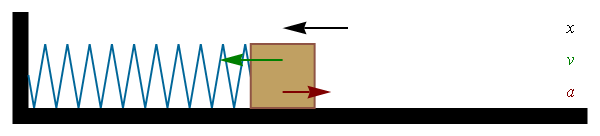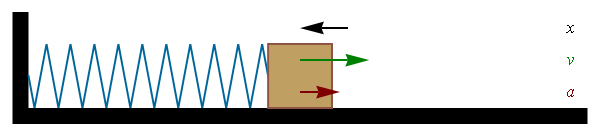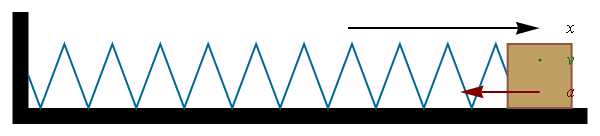
con A la amplitud de las oscilaciones,  la fase inicial o constante de fase. Este movimiento es periódico, de forma que
la fase inicial o constante de fase. Este movimiento es periódico, de forma que
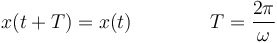
Esta solución también se puede escribir como una combinación lineal de un seno y un coseno
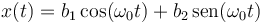
con

Los valores de las constantes b1 y b2 pueden calcularse también a partir de las condiciones iniciales del movimiento

2 Amortiguamiento
El modelo de un oscilador mecánico sometido exclusivamente a la ley de Hooke no es realista pues desprecia la presencia del rozamiento. La experiencia nos muestra que un oscilador se va frenando progresivamente hasta llegar a detenerse en la posición de equilibrio.
Esta disminución progresiva en la amplitud de las oscilaciones es debida a la presencia de rozamiento. Éste puede deberse a un roce con una superficie (rozamiento seco) o la fricción del aire o líquido que rodea al oscilador (rozamiento viscoso).
El caso del oscilador con rozamiento seco tiene un interesante análisis físico-matenático, pero no lo consideraremos aquí. En su lugar nos centraremos en el caso del rozamiento viscoso. La razón es que, aparte de ser un modelo de muchas aplicaciones, representa más adecuadamente lo que ocurre en un amortiguador mecánico.
Un amortiguador es un dispositivo como el que puede encontrarse en la suspensión de un automóvil o en una puerta con cierre automático.

Un amortiguador consta de un resorte mecánico, pero también, en el interior de éste, de un cilindro con un pistón

Si un coche no tuviera suspensión (es decir, si el chasis estuviera unido rígidamente unido al eje de las ruedas), cada bache o irregularidad en el suelo se notaría como un golpe en el interior del vehículo lo cual, además de incómodo, pone en peligro su integridad. Por otro lado, si la suspensión consistiera simplemente en un resorte casi sin rozamiento, cada bache produciría oscilaciones en el coche, incluso mucho después de haber superado el bache.
Por ello, se introduce el amortiguador. El objetivo es que el coche oscile al pasar por el bache, pero lo menos posible, de forma que retorne a la posición de equilibro en el menor tiempo posible. Esto se consigue introduciendo una fricción viscosa que disipe la energía mecánica de la oscilación. En la práctica consiste en que un fluido es obligado a pasar por una serie de válvulas de un lado a otro del pistón, frenándolo en el proceso.
La fuerza de rozamiento que experimenta el resorte se opone siempre a la velocidad de éste (si la masa va hacia la derecha, la fuerza apunta hacia la izquierda y viceversa). En primera aproximación es proporcional a la velocidad (en reposo no hay fuerza de rozamiento), por lo que se puede escribir

y para el caso particular del movimiento rectilíneo
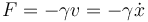
3 Ecuación del oscilador amortiguado
La segunda ley de Newton para un oscilador armónico con amortiguamiento viscoso (en una dimensión) se escribe entonces
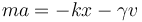
Pasando todo al primer miembro

Aplicando que la velocidad y la aceleración son las primera y segunda derivadas respecto al tiempo de la elongación nos queda la ecuación diferencial
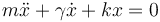
Dividiendo por la masa de la partícula podemos escribirla como

Esta es la ecuación diferencial del oscilador armónico amortiguado. La constante
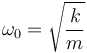
es la frecuencia propia del oscilador. Equivale a la frecuencia natural con la que oscilaría el resorte si no tuviera rozamiento. Como veremos, la presencia de rozamiento reduce la frecuencia de las oscilaciones.
La segunda constante
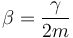
es la constante de amortiguamiento. Mide la magnitud de la fricción, siendo mayor cuanto más intensa sea ésta.
Tanto la frecuencia propia ω0 como la constante de amortiguamiento β tienen dimensiones de inversa de un tiempo y se miden en s−1 en el SI.
4 Solución de la ecuación
4.1 Caracterización de las soluciones
Antes de examinar la solución matemática de la ecuación diferencial, podemos describir como deberían ser las soluciones.
- Si el rozamiento es pequeño, debemos esperar que el resorte oscile paro con una amplitud decreciente, hasta que pasado un cierto tiempo se quede en reposo en la posición de equilibrio.
- Si el rozamiento es muy grande, en cambio, debemos esperar que no llegue a oscile, sino que simplemente se vaya moviendo lentamente hasta la posición de equilibrio.
En física siempre que una magnitud se considera grande o pequeña hay que decir comparada con qué, cuál es el patrón en que nos basamos para decir si algo es grande o pequeño. En este caso aprovechamos que tanto β como ω0 tienen las mismas dimensiones y por tanto se pueden comparar. Establecemos entonces el criterio
- Rozamiento débil: β < ω0
- Rozamiento intenso: β > ω0
La solución matemática debe reflejar por tanto un cambio de comportamiento dependiendo de como sea la constante de amortiguamiento comparada con la frecuencia propia.





