Oscilaciones amortiguadas (GIE)

De Laplace

Contenido

1 El oscilador no amortiguado
2 Amortiguamiento
3 Ecuación del oscilador amortiguado
4 Solución de la ecuación
- 4.1 Caracterización de las soluciones
- 4.2 Solución matemática
5 Caso sobreamortiguado (β > ω₀)
6 Caso subamortiguado (β < ω₀)
7 Amortiguamiento crítico (β = ω₀)
8 Comparación de los tres casos
9 Energía en un oscilador amortiguado

1 El oscilador no amortiguado

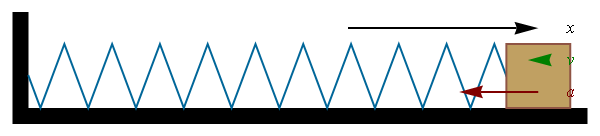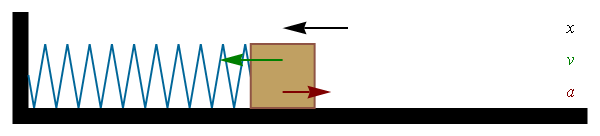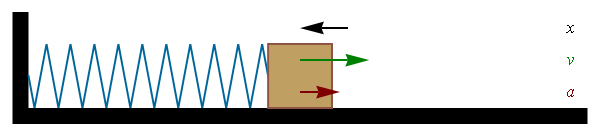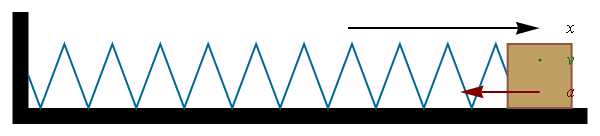
En otras secciones se estudia la cinemática y la dinámica del oscilador armónico. Éste es un sistema ideal gobernado por la ley de Hooke. Típicamente esta ley se aplica a resortes mecánicos, aunque puede generalizarse a muchas otras situaciones. En el caso de un resorte que oscila en una sola dimensión la ley de Hooke se escribe

$F = -kx\,$

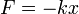
siendo $x$ la elongación del resorte (distancia respecto a la posición de equilibrio)

Una partícula sometida exclusivamente a la ley de Hooke en una dimensión cumple la ecuación de movimiento

$ma = -kx\qquad\rightarrow\qquad a= \ddot{x}=-\frac{k}{m}x$

Este es un caso particular de la ecuación para un movimiento armónico simple

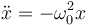
$\ddot{x} = -\omega_0^2x$

siendo en este caso la frecuencia natural

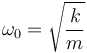
$\omega_0=\sqrt{\frac{k}{m}}$

La solución general de esta ecuación diferencial es una oscilación sinusoidal

$x(t) = A\cos(\omega_0 t+\varphi)\,$

con $A$ la amplitud de las oscilaciones, $\varphi$ la fase inicial o constante de fase. Este movimiento es periódico, de forma que

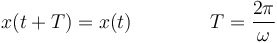
$x(t+T) = x(t)\qquad\qquad T = \frac{2\pi}{\omega}$

Esta solución también se puede escribir como una combinación lineal de un seno y un coseno

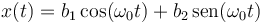
$x(t) = b_1\cos(\omega_0 t)+b_2\,\mathrm{sen}(\omega_0 t)$

con

$b_1=A\cos(\varphi) \qquad\qquad b_2 = -A\,\mathrm{sen}(\varphi)$

Los valores de las constantes $b 1$ y $b 2$ pueden calcularse también a partir de las condiciones iniciales del movimiento

$b_1= x_0 = x(t=0)\qquad\qquad b_2=\frac{v_0}{\omega_0}=\frac{v(t=0)}{\omega_0}$

2 Amortiguamiento

El modelo de un oscilador mecánico sometido exclusivamente a la ley de Hooke no es realista pues desprecia la presencia del rozamiento. La experiencia nos muestra que un oscilador se va frenando progresivamente hasta llegar a detenerse en la posición de equilibrio.

Esta disminución progresiva en la amplitud de las oscilaciones es debida a la presencia de rozamiento. Éste puede deberse a un roce con una superficie (rozamiento seco) o la fricción del aire o líquido que rodea al oscilador (rozamiento viscoso).

El caso del oscilador con rozamiento seco tiene un interesante análisis físico-matenático, pero no lo consideraremos aquí, sino en un problema. En su lugar nos centraremos en el caso del rozamiento viscoso. La razón es que, aparte de ser un modelo de muchas aplicaciones, representa más adecuadamente lo que ocurre en un amortiguador mecánico.

Un amortiguador es un dispositivo como el que puede encontrarse en la suspensión de un automóvil o en una puerta con cierre automático.

Un amortiguador consta de un resorte mecánico, pero también, en el interior de éste, de un cilindro con un pistón

Si un coche no tuviera suspensión (es decir, si el chasis estuviera unido rígidamente al eje de las ruedas), cada bache o irregularidad en el suelo se notaría como un golpe en el interior del vehículo lo cual, además de incómodo, pone en peligro su integridad. Por otro lado, si la suspensión consistiera simplemente en un resorte casi sin rozamiento, cada bache produciría oscilaciones en el coche, incluso mucho después de haber superado el bache.

Por ello, se introduce el amortiguador. El objetivo es que el coche oscile al pasar por el bache, pero lo menos posible, de forma que retorne a la posición de equilibro en el menor tiempo posible. Esto se consigue introduciendo una fricción viscosa que disipe la energía mecánica de la oscilación. En la práctica consiste en que un fluido es obligado a pasar por una serie de válvulas de un lado a otro del pistón, frenándolo en el proceso.

La fuerza de rozamiento que experimenta el resorte se opone siempre a la velocidad de éste (si la masa va hacia la derecha, la fuerza apunta hacia la izquierda y viceversa). En primera aproximación es proporcional a la velocidad (en reposo no hay fuerza de rozamiento), por lo que se puede escribir

$\vec{F}=-\gamma\vec{v}$

y para el caso particular del movimiento rectilíneo

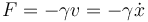
$F = -\gamma v = -\gamma\dot{x}$

3 Ecuación del oscilador amortiguado

La segunda ley de Newton para un oscilador armónico con amortiguamiento viscoso (en una dimensión) se escribe entonces

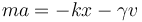
$ma = -kx-\gamma v\,$

Pasando todo al primer miembro

$ma + \gamma v + k x = 0\,$

Aplicando que la velocidad y la aceleración son las primera y segunda derivadas respecto al tiempo de la elongación nos queda la ecuación diferencial

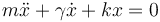
$m \ddot{x} + \gamma \dot{x}+k x = 0$

Dividiendo por la masa de la partícula podemos escribirla como

$\ddot{x}+2\beta \dot{x} +\omega_0^2 x = 0$

Esta es la ecuación diferencial del oscilador armónico amortiguado. La constante

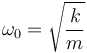
$\omega_0 = \sqrt{\frac{k}{m}}$

es la frecuencia propia del oscilador. Equivale a la frecuencia natural con la que oscilaría el resorte si no tuviera rozamiento. Como veremos, la presencia de rozamiento reduce la frecuencia de las oscilaciones.

La segunda constante

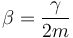
$\beta = \frac{\gamma}{2m}$

es la constante de amortiguamiento. Mide la magnitud de la fricción, siendo mayor cuanto más intensa sea ésta.

Tanto la frecuencia propia $ω 0$ como la constante de amortiguamiento $β$ tienen dimensiones de inversa de un tiempo y se miden en s⁻¹ en el SI.

4 Solución de la ecuación

4.1 Caracterización de las soluciones

Antes de examinar la solución matemática de la ecuación diferencial, podemos describir como deberían ser las soluciones.

Si el rozamiento es pequeño, debemos esperar que el resorte oscile paro con una amplitud decreciente, hasta que pasado un cierto tiempo se quede en reposo en la posición de equilibrio.

Si el rozamiento es muy grande, en cambio, esperamos que no llegue a oscilar, sino que simplemente se va moviendo lentamente hasta la posición de equilibrio.

En física siempre que una magnitud se considera grande o pequeña hay que decir comparada con qué, cuál es el patrón en que nos basamos para decir si algo es grande o pequeño. En este caso aprovechamos que tanto $β$ como $ω 0$ tienen las mismas dimensiones y por tanto se pueden comparar. Establecemos entonces el criterio

Rozamiento débil: $β < ω 0$
Rozamiento intenso: $β > ω 0$

La solución matemática debe reflejar por tanto un cambio de comportamiento dependiendo de como sea la constante de amortiguamiento comparada con la frecuencia propia.

4.2 Solución matemática

Debemos resolver la ecuación diferencial

$\ddot{x} + 2\beta \dot{x}+\omega_0^2 x = 0$

con ciertas condiciones iniciales

$x(t=0) = x_0\qquad\qquad \dot{x}(t=0)=v_0$

Esta ecuación diferencial es de las llamadas lineales (la elongación y sus derivadas no están elevadas a ninguna potencia). Para buscar una solución de una ecuación de este tipo proponemos una solución exponencial

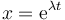
$x = \mathrm{e}^{\lambda t}\,$

Derivando esta función

$\dot{x} = \lambda \mathrm{e}^{\lambda t}\qquad\qquad \ddot{x}=\lambda^2 \mathrm{e}^{\lambda t}$

y sustituyendo en la ecuación diferencial

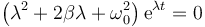
$\left(\lambda^2+2\beta\lambda + \omega_0^2\right)\mathrm{e}^{\lambda t} = 0$

Puesto que la exponencial nunca puede anularse debe cumplirse que

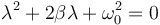
$\lambda^2+2\beta\lambda + \omega_0^2 = 0\,$

Esta ya no es una ecuación diferencial. Es una ecuación de segundo grado cuyas soluciones nos dan los valores posibles de $λ$ . Puesto que existen dos valores, la solución de la ecuación diferencial se escribe como la combinación

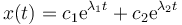
$x(t) = c_1 \mathrm{e}^{\lambda_1 t}+ c_2 \mathrm{e}^{\lambda_2 t}$

donde $c 1$ y $c 2$ son dos constantes cuyos valores se calculan a partir de las condiciones iniciales.

Resolviendo la ecuación de segundo grado nos quedan las soluciones

$\lambda_1 = -\beta + \sqrt{\beta^2-\omega_0^2}\qquad\qquad \lambda_2 = -\beta-\sqrt{\beta^2-\omega_0^2}$

Vemos que, como se dijo antes, dependiendo del valor de $β$ hay tres posibilidades, dependiendo del signo de lo que hay dentro de la raíz cuadrada

Si $β > ω 0$ las dos soluciones son reales y diferentes (caso sobreamortiguado).
Si $β = ω 0$ existe una solución real doble (amortiguamiento crítico).
Si $β < ω 0$ las dos soluciones son complejas conjugadas (caso subamortiguado).

Cada uno de estos casos merece un estudio por separado.

5 Caso sobreamortiguado (β > ω₀)

Consideraremos en primer lugar el caso de rozamiento intenso

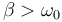
$\beta > \omega _0\,$

En este caso las dos raíces de la ecuación son reales y además negativas

$\lambda_1 = -\beta + \sqrt{\beta^2-\omega_0^2}\qquad \qquad \lambda_2 = -\beta -\sqrt{\beta^2-\omega_0^2}$

(para ver que la primera es negativa basta con observar que la raíz es menor que $β$ ). La solución de la ecuación diferencial es entonces una suma de dos exponenciales decrecientes

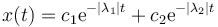
$x(t) = c_1 \mathrm{e}^{-|\lambda_1| t}+c_2 \mathrm{e}^{-|\lambda_2| t}$

Puesto que $| λ 2 | > | λ 1 |$ la segunda exponencial decae más rápidamente, y es la primera de las dos la que determina el tiempo en decaer.

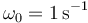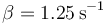Por dar un ejemplo numérico, supongamos que $\omega_0=1\,\mathrm{s}^{-1}$ y que $\beta=1.25\,\mathrm{s}^{-1}$ . En ese caso resultan

$\lambda_1=-0.5\,\mathrm{s}^{-1}\qquad \qquad \lambda_1=-2.0\,\mathrm{s}^{-1}$

Esto quiere decir que la primera exponencial decae en un tiempo típico de 2 segundos (la inversa de $λ 1$ ) mientras que la segunda lo hace en medio segundo, por tanto al cabo de un segundo prácticamente ya solo tenemos la primera exponencial.

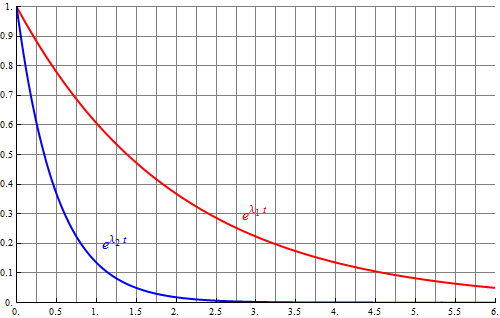
La solución completa es la combinación de las dos aunque rápidamente se asemeja mucho a la primera

El caso de esta figura representa la situación en que se tira del oscilador y se libera desde el reposo (siendo nula su velocidad inicial, lo que corresponde a una tangente horizontal). El resorte tiende lentamente a la posición de equilibrio.

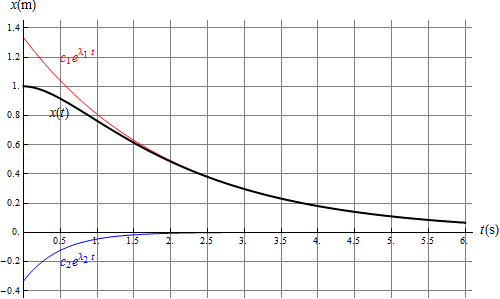
El que la solución sea una combinación de exponenciales decrecientes no quiere decir que la solución sea decreciente en todo instante. Por ejemplo, imaginemos el caso de un muelle que es golpeado en la posición de equilibrio. La masa se aleja originalmente de la posición de equilibrio, para luego retornar lentamente a ella.

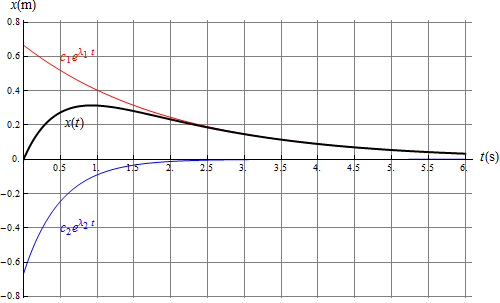
6 Caso subamortiguado (β < ω₀)

El caso opuesto al anterior lo obtenemos cuando el rozamiento es débil (incluyendo el caso en que no hay rozamiento).

Si llamamos

$\omega = \sqrt{\omega_0^2-\beta^2}$

podemos escribir las dos soluciones de la ecuación de segundo grado como complejos conjugados

$\lambda_1 = -\beta+\mathrm{j}\omega \qquad\qquad \lambda_2 = -\beta -\mathrm{j}\omega\,$

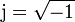siendo $\mathrm{j}=\sqrt{-1}$ la unidad imaginaria. La solución general de la ecuación diferencial queda entonces

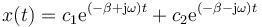
$x(t) = c_1 \mathrm{e}^{(-\beta + \mathrm{j}\omega)t}+ c_2 \mathrm{e}^{(-\beta - \mathrm{j}\omega)t}\,$

Aquí podemos extraer como factor común la parte real de la exponencial y escribir

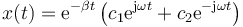
$x(t)=\mathrm{e}^{-\beta t}\left(c_1 \mathrm{e}^{\mathrm{j}\omega t}+ c_2 \mathrm{e}^{-\mathrm{j}\omega t}\right)$

Para ver que esta solución representa oscilaciones amortiguadas aplicamos la fórmula de Euler

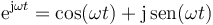
$\mathrm{e}^{\mathrm{j}\omega t} = \cos(\omega t) + \mathrm{j}\,\mathrm{sen}(\omega t)$

que transforma la solución en

$x(t) = \mathrm{e}^{-\beta t}\left(b_1\cos(\omega t) + b_2\,\mathrm{sen}(\omega t)\right)$

con

$b_1 = c_1+c_2 \qquad \qquad b_2 = \mathrm{j}(c_1-c_2)$

Esta combinación de senos y cosenos puede reducirse a uno solo, como se hace el caso del oscilador sin rozamiento, y escribir la solución en la forma

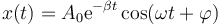
$x(t) = A_0\mathrm{e}^{-\beta t}\cos(\omega t+\varphi)$

Podemos leer esta solución como una oscilación sinusoidal

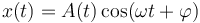
$x(t) = A(t) \cos(\omega t+\varphi)$

con una amplitud que decae exponencialmente

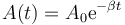
$A(t) = A_0\mathrm{e}^{-\beta t}\,$

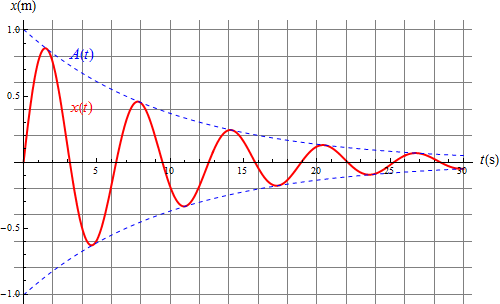
Este comportamiento se dice cuasiperiódico, porque no llega a repetirse (al completar una oscilación no se encuentra en la misma posición que al iniciarla). El cuasiperiodo es mayor que el del oscilador sin rozamiento

$\omega < \omega_0\qquad\Rightarrow\qquad T = \frac{2\pi}{\omega} > \frac{2\pi}{\omega_0} = T_0$

El tiempo que tarda en decaer la amplitud no los da el factor de decaimiento $β$ . En un tiempo

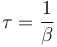
$\tau = \frac{1}{\beta}$

la amplitud se reduce en un factor e (a un 36.8% de la que tuviera). Tenemos entonces dos escalas de tiempo: $T 0$ nos mide el tiempo que tarda en oscilar, $τ$ el tiempo que tarda en amortiguarse. El cociente adimensional

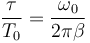
$\frac{\tau}{T_0}=\frac{\omega_0}{2\pi \beta}$

nos mide la importancia del amortiguamiento pues nos da el número de oscilaciones en un tiempo típico de decaimiento. Si este número es grande quiere decir que el oscilador es muy poco amortiguado.

Comparando las oscilaciones con y sin rozamiento vemos que si éste es pequeño se nota un cambio apreciable en la amplitud, pero muy pequeño en el peridoo

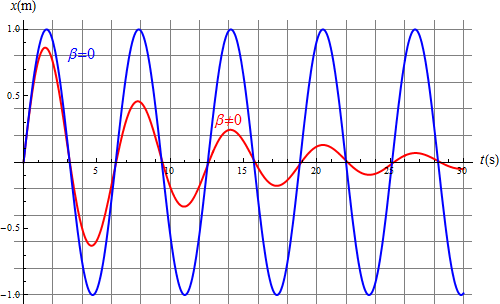
Si el rozamiento es grande, de forma que 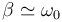$\beta \simeq \omega_0$ el decaimiento es muy importante y el periodo de oscilación es tan largo que prácticamente la partícula no llega a realizar ninguna oscilación.

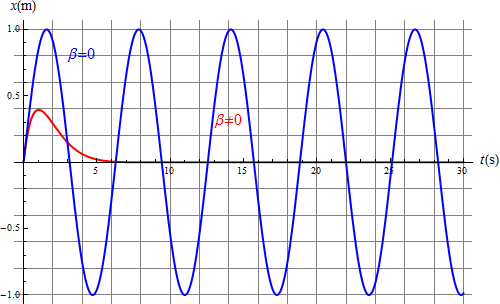
En el ejemplo de la figura ( $β = 0.9ω 0$ ) el primer mínimo está por debajo del eje solo -0.0006m y es inapreciable en la gráfica.

7 Amortiguamiento crítico (β = ω₀)

El tercer caso es uno particular que debe seleccionarse modificando las propiedades del sistema, ya que requiere unos valores concretos de los parámetros. Para el caso del muelle con rozamiento debe cumplirse

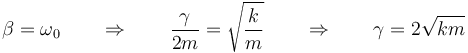
$\beta = \omega_0 \qquad\Rightarrow\qquad \frac{\gamma}{2m}=\sqrt{\frac{k}{m}}\qquad\Rightarrow\qquad \gamma = 2\sqrt{km}$

La constante de rozamiento debe tener este valor exacto. Si es un poco mayor ya el movimiento es sobreamortiaguado; si es un poco menor, subamortiguado.

En el caso del amortiguamiento crítico, puede demostrarse que la solución es de la forma

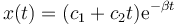
$x(t) = (c_1+c_2t)\mathrm{e}^{-\beta t}\,$

Gráficamente esta función presenta un decaimiento exponencial, similar al caso sobreamortiguado.

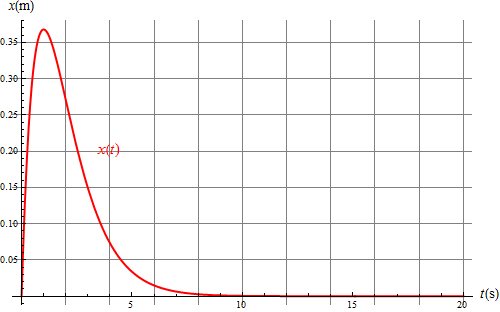
El amortiguamiento crítico posee una propiedad que lo hace interesante desde el punto de vista técnico: es el caso en que se retorna más rápidamente a la posición de equilibrio. Si la fricción es menor, el oscilador va y viene y tarda más en pararse. Si es mayor, la fuerte fricción ralentiza el movimiento y tarda también más en pararse. El tiempo típico de parada en el caso subamortiguado es

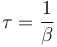
$\tau = \frac{1}{\beta}$

y en el sobreamortiguado

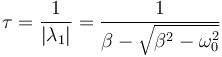
$\tau = \frac{1}{|\lambda_1|}=\frac{1}{\beta-\sqrt{\beta^2-\omega_0^2}}$

Representando este tiempo como función de $β$ para una frecuencia propia fijada de 1 s⁻¹ vemos como efectivamente es mínimo cuando se da el amortiguamiento crítico.

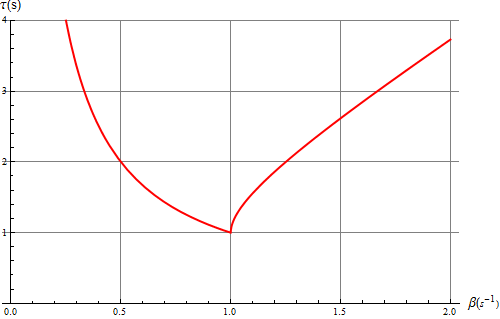
Por ello, los amortiguadores de los automóviles y demás maquinaria procuran ajustarse al valor crítico, ya que de esta forma se consigue el objetivo de detener las vibraciones en el menor tiempo posible.

8 Comparación de los tres casos

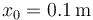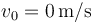Supongamos, como ejemplo, una frecuencia propia de 1\,rad/s y que las condiciones iniciales son que liberamos la partícula desde una cierta distancia de 10 cm, es x_0 decir $x_0=0.1\,\mathrm{m}$ y $v_0=0\,\mathrm{m}/\mathrm{s}$ . Comparando los caso de $β = 0.5s - 1$ , $β = 1.0s - 1$ , y $β = 1.5s - 1$ obtenemos las curvas siguientes:

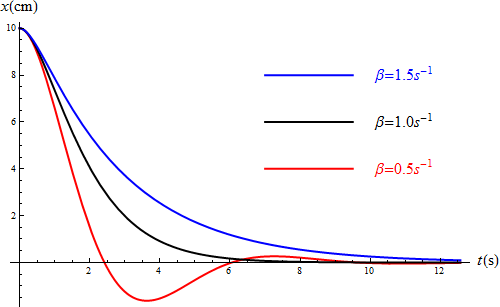
Vemos como la crítica y la sobreamortiguada decaen siendo la crítica más rápida en hacerlo, mientras que la subamortiguada presenta oscilaciones rápidamente decrecientes.

Si consideramos el caso de una masa que parte del equilibrio, pero con una cierta velocidad de 1m/s (es decir 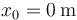$x_0=0\,\mathrm{m}$ , $v_0 =1\,\mathrm{m}/\mathrm{s}$ obtenemos para los mismos valores

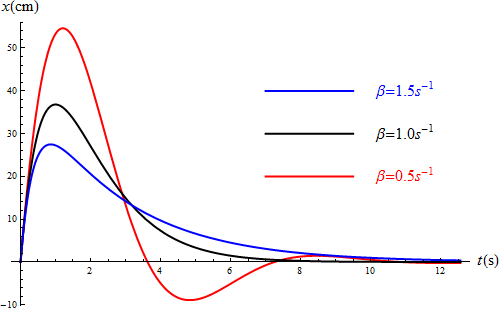
En este caso las curvas no se limitan a decaer, pues hay un alejamiento inicial. La partícula termina volviendo a la posición de equilibrio, siendo el camino más rápido el del amortiguamiento crítico. Vemos también que aunque en todos los casos parte con la misma velocidad el máximo alejamiento es menor cuanto mayor sea el rozamiento.

9 Energía en un oscilador amortiguado

Una de las consecuencias del amortiguamiento es la disipación de energía mecánica. De acuerdo con el teorema de las fuerzas vivas

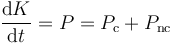
$\frac{\mathrm{d}K}{\mathrm{d}t}=P=P_\mathrm{c}+P_\mathrm{nc}$

siendo $K$ la energía cinética

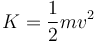
$K = \frac{1}{2}mv^2$

y $P c$ la potencia de las fuerzas conservativas (la elástica, en este caso) y $P n c$ la de las no conservativas (que sería la de rozamiento). La potencia de las fuerzas conservativas verifica

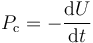
$P_\mathrm{c} = -\frac{\mathrm{d}U}{\mathrm{d}t}$

con $U$ la energía potencial elástica

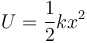
$U=\frac{1}{2}kx^2$

Pasando la energía potencial al primer miembro obtenemos la energía mecánica

$\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}(K+U) = P_\mathrm{nc}$

La potencia de las fuerzas no conservativas la calculamos multiplicando la fuerza por la velocidad

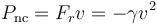
$P_\mathrm{nc}=F_rv = -\gamma v^2\,$

de forma que nos queda la relación

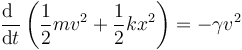
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{1}{2}mv^2+\frac{1}{2}kx^2\right)=-\gamma v^2$

Puesto que el segundo miembro es siempre negativo, esta ecuación nos dice que la energía mecánica se va disipando progresivamente, aunque no a ritmo uniforme: el consumo es mayor cuando lo es la rapidez del movimiento.

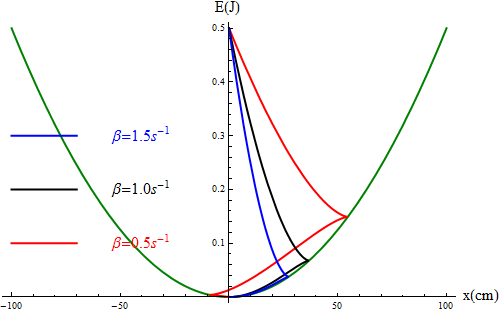
En el caso del amortiguamiento muy débil, si representamos la energía mecánica en una curva de potencial vemos como la energía mecánica va descendiendo a medida que la partícula va y viene

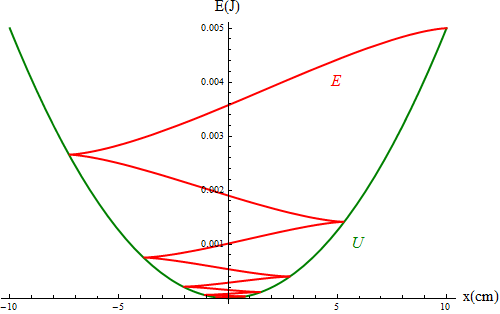
Si realizamos gráficas equivalentes para los ejemplos anteriores vemos un decaimiento muy rápido de la energía. Puesto que en el caso crítico y el sobreamortiguado no llega a realizar una oscilación completa, lo que vemos es que la curva de energía "cae en picado", siendo la disipación tanto más rápida cuanto mayor es la constante de amortiguamiento.

Oscilaciones amortiguadas (GIE)

De Laplace

Contenido

1 El oscilador no amortiguado

2 Amortiguamiento

3 Ecuación del oscilador amortiguado

4 Solución de la ecuación

4.1 Caracterización de las soluciones

4.2 Solución matemática

5 Caso sobreamortiguado (β > ω₀)

6 Caso subamortiguado (β < ω₀)

7 Amortiguamiento crítico (β = ω₀)

8 Comparación de los tres casos

9 Energía en un oscilador amortiguado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Oscilaciones amortiguadas (GIE)

De Laplace

Contenido

1 El oscilador no amortiguado

2 Amortiguamiento

3 Ecuación del oscilador amortiguado

4 Solución de la ecuación

4.1 Caracterización de las soluciones

4.2 Solución matemática

5 Caso sobreamortiguado (β > ω0)

6 Caso subamortiguado (β < ω0)

7 Amortiguamiento crítico (β = ω0)

8 Comparación de los tres casos

9 Energía en un oscilador amortiguado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

5 Caso sobreamortiguado (β > ω₀)

6 Caso subamortiguado (β < ω₀)

7 Amortiguamiento crítico (β = ω₀)