Oscilaciones amortiguadas (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==El oscilador no amortiguado== ==Amortiguamiento== ==Ecuación del oscilador amortiguado== ==Solución de la ecuación== ==Caso sobreamortiguado== ==Caso subamortiguado== ==Amo…') |
(→El oscilador no amortiguado) |
||
| Línea 1: | Línea 1: | ||
==El oscilador no amortiguado== | ==El oscilador no amortiguado== | ||
| + | En otras secciones se estudia la [[Cinemática_del_movimiento_rectilíneo_(GIE)#Arm.C3.B3nico_simple|cinemática]] y la [[Aplicaciones_de_las_leyes_de_Newton_(GIE)#Oscilador_arm.C3.B3nico|dinámica]] del oscilador armónico. Éste es un sistema ideal gobernado por la ley de Hooke. Típicamente esta ley se aplica a resortes mecánicos, aunque puede generalizarse a muchas otras situaciones. En el caso de un resorte que oscila en una sola dimensión la ley de Hooke se escribe | ||
| + | |||
| + | <center><math>F = -kx\,</math></center> | ||
| + | |||
| + | siendo <math>x</math> la ''elongación'' del resorte (distancia respecto a la posición de equilibrio) | ||
| + | |||
| + | Una partícula sometida exclusivamente a la ley de Hooke en una dimensión cumple la ecuación de movimiento | ||
| + | |||
| + | <center><math>ma = -kx\qquad\rightarrow\qquad a= \ddot{x}=-\frac{k}{m}x</math></center> | ||
| + | |||
| + | Este es un caso particular de la ecuación para un movimiento armónico simple | ||
| + | |||
| + | <center><math>\ddot = -\omega_0^2x</math></center> | ||
| + | |||
| + | siendo en este caso la frecuencia natural | ||
| + | |||
| + | \omega | ||
| + | |||
| + | |||
| + | <center>[[Archivo:Muelle.gif]]</center> | ||
| + | |||
==Amortiguamiento== | ==Amortiguamiento== | ||
==Ecuación del oscilador amortiguado== | ==Ecuación del oscilador amortiguado== | ||
Revisión de 10:57 6 dic 2012
Contenido |
1 El oscilador no amortiguado
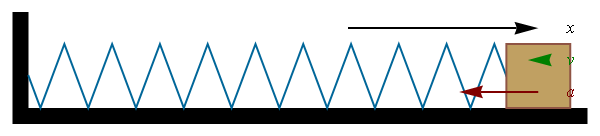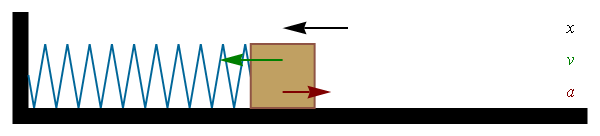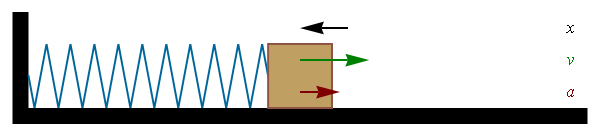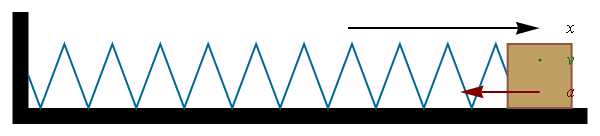
En otras secciones se estudia la cinemática y la dinámica del oscilador armónico. Éste es un sistema ideal gobernado por la ley de Hooke. Típicamente esta ley se aplica a resortes mecánicos, aunque puede generalizarse a muchas otras situaciones. En el caso de un resorte que oscila en una sola dimensión la ley de Hooke se escribe
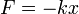
siendo x la elongación del resorte (distancia respecto a la posición de equilibrio)
Una partícula sometida exclusivamente a la ley de Hooke en una dimensión cumple la ecuación de movimiento

Este es un caso particular de la ecuación para un movimiento armónico simple
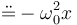
siendo en este caso la frecuencia natural
\omega