Problemas de cinemática del sólido rígido (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Ejemplo de campo de velocidades de un sólido== El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional <center><math>…') |
(→Clasificación de movimientos de un sólido) |
||
| Línea 64: | Línea 64: | ||
|} | |} | ||
| - | # Identifique cuáles de las situaciones anteriores son compatibles con | + | # Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez. |
| - | la condición de rigidez. | + | # Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal. |
| - | # Para las que sí lo son, identifique si se trata de un | + | # Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD. |
| - | movimiento de traslación pura, rotación pura o helicoidal. | + | # Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas. |
| - | # Para las rotaciones y movimientos helicoidales, determine la | + | |
| - | posición del EIR o EIRMD. | + | |
| - | # Para los movimientos compatibles, calcule la cantidad de | + | |
| - | movimiento, el momento cinético y la energía cinética del sistema de | + | |
| - | masas. | + | |
Revisión de 11:45 14 dic 2011
1 Ejemplo de campo de velocidades de un sólido
El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional
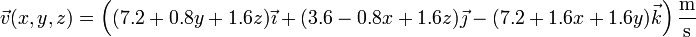
- Determine la velocidad angular,
 , y la velocidad del origen de coordenadas,
, y la velocidad del origen de coordenadas,  .
.
- Halle la velocidad del punto
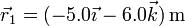 .
.
- ¿Qué tipo de movimiento describe el sólido en este instante?
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).
2 Movimiento de un sólido conocido un eje
Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 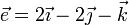 , de tal forma que la velocidad del punto B(0,2,1) es
, de tal forma que la velocidad del punto B(0,2,1) es 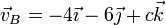
- Halle el valor de la constante c.
- Calcule la velocidad angular instantánea.
- Calcule la velocidad del punto P(1,1,0).
Todas las cantidades están expresadas en las unidades del SI.
3 Clasificación de movimientos de un sólido
Se tiene un sólido formado por ocho masas iguales, 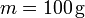 , situadas en los vértices de un cubo de lado
, situadas en los vértices de un cubo de lado 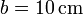 . En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
Considere los casos siguientes para las velocidades de las masas situadas en 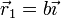 ,
, 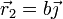 y
y 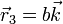
| Caso | 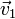 (cm/s) (cm/s)
| 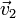 (cm/s) (cm/s)
| 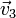 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 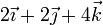
| 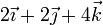
| 
|
| II | 
| 
| 
|
| III | 
| 
| 
|
| IV | 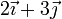
| 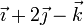
| 
|
| V | 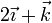
| 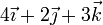
| 
|
| VI | 
| 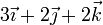
| 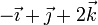
|
- Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
- Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
- Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
- Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.





