Problemas de dinámica del punto material (G.I.T.I.)

De Laplace

Revisión de 18:48 13 oct 2010

1 Caída libre de un cuerpo

Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia.

1. Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente, partiendo del reposo desde una altura h = 2 km, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s².
2. Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura z arbitraria.
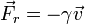
3. Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma 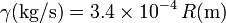siendo γ una constante de fricción que para una esfera en aire es de valor con R el radio de la partícula. Si se incluye esta fuerza, ¿qué ecuación de movimiento resulta para la velocidad vertical?
4. Razone que, partiendo de la ecuación anterior, resulta que la velocidad tiende a un valor límite.
5. Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿Con qué velocidad llega al suelo? ¿Cuánto tarda en caer? ¿Cuánta energía mecánica se pierde por el camino?
6. Determine la expresión exacta de la velocidad y la altura como función del tiempo

2 Tensión de un péndulo

Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo de masa m y longitud l₀ pasa por su punto más bajo, como función del ángulo máximo θ₀ con el que se separa de la vertical.

Determine la tensión de la cuerda en el punto más bajo y el punto de máxima amplitud.

3 Partícula sometida a fuerza magnética

Una partícula con carga q y masa m inmersa en un campo magnético uniforme experimenta una fuerza

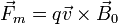
Supongamos que la partícula posee inicialmente una velocidad perpendicular al campo .

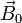1. Demuestre que la energía cinética de la partícula es constante.
2. Pruebe que la mase se mueve en una trayectoria plana.
3. Determine el radio de curvatura de la trayectoria. ¿Qué tipo de movimiento describe una carga en un movimiento uniforme?

4 Caída a lo largo de una hélice

Una pequeña anilla de masa m esta obligada a moverse a lo largo de una hélice de radio A y paso de rosca b cuyo eje está situado verticalmente. La anilla se encuentra sometida a la acción de la gravedad y parte del reposo desde una altura h. Cuando se encuentra a una altura z, ¿con qué velocidad se mueve? ¿Qué fuerza ejerce la anilla sobre la hélice?

5 Cálculo de energías potenciales

Para las siguientes fuerzas, consideradas en una dimensión

• Peso: F = − mg
• Elástica: F = − k(x − l₀)
• Gravitatoria: F = − GMm / x²

1. Determine la energía potencial de la que derivan.
2. Trace las curvas de potencial para las tres fuerzas.
3. Considere el caso de una partícula sometida simultáneamente a una fuerza elástica y al peso, ¿cuál es la energía potencial como función de la posición? ¿Qué forma tiene su curva de potencial? ¿Qué movimiento describe una partícula sometida a estas dos fuerzas a la vez?

6 Movimiento rectilíneo por tramos

Una partícula de masa m, realiza un movimiento rectilíneo sobre la parte positiva de un eje cartesiano OX. Cuando la distancia entre la partícula y el origen O supera una cierta longitud b conocida, la partícula es atraída hacia O por una fuerza de módulo mk / x² (siendo k una constante); pero, sin embargo, cuando x < b, la partícula es repelida desde O por una fuerza de módulo mbk / x³.

1. Determine y represente gráficamente la energía potencial de la partícula en función de su coordenada x (considerando que dicha función es nula en el infinito y exigiendo su continuidad en x = b).
2. Sabiendo que la partícula inicia su movimiento desde el reposo instantáneo en el punto P₀ de coordenada x = 2b, determine su energía mecánica.
3. ¿En qué otro punto alcanzará la partícula el reposo instantáneo (punto de retorno)? ¿Cuánto tiempo tardará en llegar desde x = b hasta dicho punto?

7 Partícula en el interior de un aro

Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula situada en el punto más bajo del aro si se quiere que llegue al punto más alto si la partícula es:

1. Una anilla ensartada en el aro
2. Una bolita que desliza por el interior del aro, sin estar unida a él.

Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores.

8 Partícula que desliza sobre una esfera

Una partícula P, de masa m, es abandonada en reposo en el punto más alto de una esfera de radio R que descansa apoyada en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determine el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo.

9 Efecto de la rotación en la gravedad aparente

Estudie la influencia del movimiento de rotación propia de la Tierra sobre el peso aparente de un objeto próximo a su superficie en función de la latitud λ. Si la aceleración de caída libre de un objeto a nivel del mar medida respecto a la superficie terrestre vale 9.78 m/s^2 en el ecuador, ¿cuánto vale allí la aceleración de la gravedad?

10 Partícula sujeta de dos hilos

Una masa m = 10 kg cuelga inicialmente de un hilo de 50 cm de longitud sujeto del techo a una distancia de 80 cm de la pared más cercana. Para evitar que el primer hilo se rompa, se afianza la masa sujetándola con un hilo adicional de 50 cm atado horizontalmente a la pared. Determine la tensión de cada hilo. ¿Ha aumentado o disminuido la tensión del hilo original?

11 Equilibrio de partícula en parábola

Una partícula de masa m se encuentra sometida simultáneamente a su peso y la fuerza atractiva de un resorte de constante k y longitud natural nula anclado en el punto 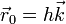. La partícula está ensartada en la parábola z = bx².

1. Determine la(s) posición(es) de equilibrio de la masa sobre la parábola.
2. Calcule la fuerza de reacción vincular de la parábola sobre la partícula en la(s) posición(es) de equilibrio.
3. Trace la curva de la energía potencial como función de la coordenada x y discuta la estabilidad de las posibles posiciones de equilibrio.

12 Oscilador armónico en el plano

Una partícula de masa m se encuentra sujeta a un resorte de constante k y longitud natural nula, que ejerce una fuerza

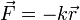
La posición inicial de la masa y su velocidad inicial son:

        

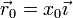
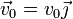
1. Demuestre que el movimiento de esta partícula se restringe al plano OXY
2. Exprese el momento cinético de la partícula en función de x, y y sus derivadas temporales, 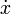y 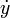. ¿A qué es igual esta cantidad, teniendo en cuenta las condiciones iniciales?
3. Exprese la energía cinética, la potencial y la energía mecánica de la partícula en función de x, y, 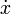y .
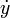4. Demuestre que la energía mecánica es constante y halle su valor en función de las condiciones iniciales.