Partícula sometida a fuerza magnética

De Laplace

Contenido

1 Enunciado
2 Energía cinética
3 Componente paralela
4 Componente ortogonal
5 Caso P₂ = 0
6 Caso P₁ = 0

1 Enunciado

Sea una partícula con carga $q$ y masa $m$ sometida exclusivamente a un campo magnético uniforme y constante, de forma que experimenta la fuerza

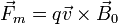
$\vec{F}_m = q\vec{v}\times\vec{B}_0$

Supongamos que la partícula posee una velocidad inicial $\vec{v}_0$

Demuestre que la energía cinética de la partícula es una integral primera.
Demuestre que el producto 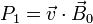$P_1 = \vec{v}\cdot\vec{B}_0$ es también una constante de movimiento.
De acuerdo con lo anterior, ¿es 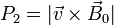$P_2 = |\vec{v}\times\vec{B}_0|$ una integral primera?
Suponga que $P_1 \neq 0$ y $P 2 = 0$ , ¿qué representa en términos de la velocidad inicial? ¿Qué tipo de movimiento describe la partícula en este caso?
Suponga ahora P₁ = 0 y ,
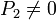1. ¿A qué tipo de velocidad inicial corresponde?
2. Demuestre que en este caso la trayectoria es plana.
3. Calcule el radio de curvatura de la trayectoria. ¿Qué tipo de movimiento describe la partícula?

2 Energía cinética

La energía cinética de la carga es

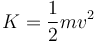
$K = \frac{1}{2}mv^2$

Para ver que es una integral primera, derivamos respecto al tiempo

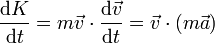
$\frac{\mathrm{d}K}{\mathrm{d}t}=m\vec{v}\cdot\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}= \vec{v}\cdot(m\vec{a})$

Sustituyendo aquí la fuerza magnética

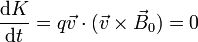
$\frac{\mathrm{d}K}{\mathrm{d}t}=q\vec{v}\cdot(\vec{v}\times\vec{B}_0)=0$

Puesto que la fuerza es puramente normal en todo momento, la potencia desarrollada por ella es nula y la energía cinética permanece constante. Ello implica que el movimiento de una carga en un campo magnético es siempre uniforme.

3 Componente paralela

La cantidad

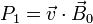
$P_1 = \vec{v}\cdot\vec{B}_0$

es proporcional a la componente de la velocidad paralela al campo magnético

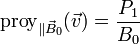
$\mathrm{proy}_{\parallel\vec{B}_0}(\vec{v}) = \frac{P_1}{B_0}$

De nuevo, para ver que es una integral primera, derivamos respecto al tiempo

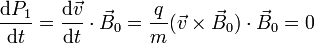
$\frac{\mathrm{d}P_1}{\mathrm{d}t}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\cdot\vec{B}_0= \frac{q}{m}(\vec{v}\times\vec{B}_0)\cdot\vec{B}_0 = 0$

Puesto que la derivada es nula, $P 1$ es una integral primera. Geométricamente, esto quiere decir que la proyección de la velocidad en la dirección del campo magnético se mantiene constante en todo momento.

4 Componente ortogonal

La cantidad $P 2$

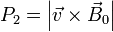
$P_2 = \left|\vec{v}\times\vec{B}_0\right|$

es proporcional a la proyección ortogonal de la velocidad sobre el campo magnético

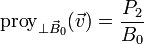
$\mathrm{proy}_{\perp\vec{B}_0}(\vec{v}) = \frac{P_2}{B_0}$

La constancia de $P 2$ se deduce de la de $P 1$ y de la energía cinética $K$ . Tenemos que, por un lado

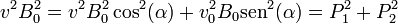
$v^2 B_0^2 = v^2B_0^2\cos^2(\alpha) + v_0^2B_0\mathrm{sen}^2(\alpha) = P_1^2 + P_2^2$

y por otro lado

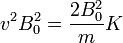
$v^2B_0^2 = \frac{2B_0^2}{m}K$

y por tanto

$P_2 = \sqrt{\frac{2B_0^2}{m}K-P_1^2}$

Si $K$ y $P 1$ son integrales primeras, $P 2$ también lo es. Geométricamente, tenemos que la velocidad tiene un componente paralela y una ortogonal. Puesto que el módulo de la velocidad es constante y la proyección paralela tampoco varía en el tiempo, resulta que la magnitud de la componente normal permanece invariable, aunque su dirección pueda ir cambiando.

5 Caso P₂ = 0

El caso $P 2 = 0$ corresponde a que la velocidad inicial no tiene componente ortogonal a 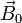$\vec{B}_0$ , esto es, se trata de una velocidad inicial paralela al campo magnético.

La constancia de $P 2$ implica que la velocidad siempre es paralela al campo magnético. Puesto que la rapidez también permanece constante, se deduce que la velocidad permanece constante en módulo dirección y sentido

$\vec{v}=\vec{v}_0 = \mathrm{cte}$

y el movimiento resultante es rectilíneo y uniforme en la dirección del campo magnético.

6 Caso P₁ = 0

En este caso no hay componente de la velocidad paralela al campo magnético. Esto corresponde a una velocidad inicial perpendicular al campo magnético.

La constancia de $P 1$ implica que la velocidad es siempre perpendicular a 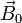$\vec{B}_0$ . La aceleración también lo es. Por tanto, el producto vectorial de $\vec{v}$ y $\vec{a}$ tiene siempre la dirección paralela al campo magnético, el vector binormal es constante y la trayectoria es plana.

Por otro lado, puesto que la fuerza es siempre perpendicular a la velocidad, la aceleración es normal en todo momento y

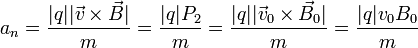
$a_n = \frac{|q||\vec{v}\times\vec{B}|}{m} = \frac{|q|P_2}{m} = \frac{|q||\vec{v}_0\times\vec{B}_0|}{m} = \frac{|q|v_0B_0}{m}$

El radio de curvatura en cada instante será igual a

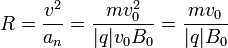
$R = \frac{v^2}{a_n} = \frac{mv_0^2}{|q|v_0B_0} = \frac{mv_0}{|q|B_0}$

Este radio es constante y por tanto la carga describe un movimiento circular uniforme.

El valor del radio de la circunferencia, proporcional a la cantidad de movimiento de la partícula, se denomina radio de Larmor y es esencial en el descubrimiento de nuevas partículas. La velocidad angular de giro es, en módulo,

$\omega = \frac{v_0}{R} = \frac{|q|B_0}{m}$

Esta cantidad se conoce en física de partículas como frecuencia ciclotrón.

En el caso general en que ni $P 1$ ni $P 2$ sean nulas, el movimiento resultante es una combinación de los dos anteriores: un avance a velocidad constante en la dirección del campo magnético, acompañado de un giro uniforme alrededor de él, resultando un movimiento helicoidal.

Partícula sometida a fuerza magnética

De Laplace

Contenido

1 Enunciado

2 Energía cinética

3 Componente paralela

4 Componente ortogonal

5 Caso P₂ = 0

6 Caso P₁ = 0

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Partícula sometida a fuerza magnética

De Laplace

Contenido

1 Enunciado

2 Energía cinética

3 Componente paralela

4 Componente ortogonal

5 Caso P2 = 0

6 Caso P1 = 0

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

5 Caso P₂ = 0

6 Caso P₁ = 0