Caída libre de un cuerpo

De Laplace

Contenido

1 Enunciado
2 Tiempo y velocidad sin rozamiento
3 Energía sin rozamiento
4 Ecuación diferencial
5 Velocidad límite
6 Caída a la velocidad límite
7 Velocidad y posición con rozamiento

1 Enunciado

Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia.

Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.50 mm que cae verticalmente, partiendo del reposo desde una altura h = 2 km, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s².
Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura $z$ arbitraria.
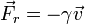
Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma 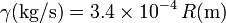$\vec{F}_r=-\gamma\vec{v}$ siendo $γ$ una constante de fricción que para una esfera en aire es de valor $\gamma(\mathrm{kg}/\mathrm{s}) = 3.4\times 10^{-4}\,R(\mathrm{m})$ con $R$ el radio de la partícula. Si se incluye esta fuerza, ¿qué ecuación diferencial resulta para la velocidad vertical?
Razone que, partiendo de la ecuación anterior, se llega a que la velocidad tiende a un valor límite.
Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿con qué velocidad llega al suelo? ¿Cuánto tarda en caer? ¿Cuánta energía mecánica se pierde por el camino?
Determine la expresión exacta de la velocidad y la altura como función del tiempo

2 Tiempo y velocidad sin rozamiento

Supondremos en primer lugar que no existe fricción con el aire. En ese caso, la única fuerza actuando sobre la partícula es el peso, de forma que la ecuación de movimiento

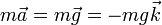
$m\vec{a}=m\vec{g}=-mg\vec{k}$

En principio, la masa inercial no tiene por qué coincidir con la que aparece en el peso. Sin embargo, Galileo mostró que eran iguales y que todos los cuerpos caen la misma aceleración

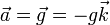
$\vec{a}=\vec{g}=-g\vec{k}$

Las condiciones iniciales para este problema son

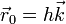
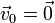
$\vec{r}_0 = h\vec{k}$ $\vec{v}_0=\vec{0}$

La integración de esta sistema es inmediata. Integrando una vez

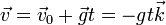
$\vec{v}=\vec{v}_0+\vec{g}t = -gt\vec{k}$

y una segunda vez

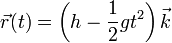
$\vec{r}(t) = \left(h-\frac{1}{2}gt^2\right)\vec{k}$

La partícula describe un movimiento rectilíneo uniformemente acelerado, aumentando la celeridad linealmente con el tiempo. La partícula impacta contra el suelo cuando $z = 0$ lo cual ocurre para

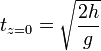
$t_{z=0}= \sqrt{\frac{2h}{g}}$

y la velocidad en ese momento

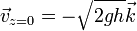
$\vec{v}_{z=0}=-\sqrt{2gh}\vec{k}$

La componente vertical de la velocidad es negativa pues va dirigida hacia abajo. La celeridad en el momento de impacto es

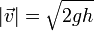
$\left|\vec{v}\right| = \sqrt{2gh}$

Para una altura de inicial de 2 km, se obtiene aproximadamente un tiempo de caída de 20 s y una celeridad de impacto de 200 m/s. Es evidente que no es esta la celeridad con la que una gota de lluvia (o un paracaidista) llega al suelo. Un cálculo correcto debe tener en cuenta la fricción con el aire.

3 Energía sin rozamiento

La energía cinética es igual a

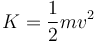
$K = \frac{1}{2}mv^2$

En el instante inicial, la partícula se encuentra en reposo y

$K = 0\,\mathrm{J}\qquad (z=h)$

En el momento del impacto

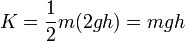
$K = \frac{1}{2}m(2gh) = mgh$

Para hallar el valor numérico necesitamos la masa de la partícula. Para una esfera de agua de radio 0.50 mm su masa es

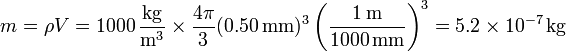
$m = \rho V =1000\,\frac{\mathrm{kg}}{\mathrm{m}^3}\times\frac{4\pi}{3}(0.50\,\mathrm{mm})^3\left(\frac{1\,\mathrm{m}}{1000\,\mathrm{mm}}\right)^3 = 5.2\times10^{-7}\,\mathrm{kg}$

lo que nos da una energía cinética final

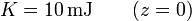
$K = 10\,\mathrm{mJ}\qquad(z=0)$

La energía potencial la obtenemos integrando la fuerza desde el origen de potencial hasta una cierta posición. La fuerza que actúa sobre la partícula es su peso

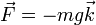
$\vec{F}=-mg\vec{k}$

Si tomamos como origen de energías el suelo ( $z = 0$ ) la energía potencial a una cierta altura es

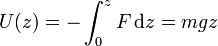
$U(z)=-\int_0^z F\,\mathrm{d}z = mgz$

En el instante inicial $z = h$ y

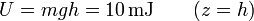
$U = mgh = 10\,\mathrm{mJ}\qquad (z=h)$

En el instante final, su altura es nula y

$U = 0\,\mathrm{J}\qquad (z=0)$

La energía mecánica es suma de las dos anteriores. Esta suma posee un valor constante

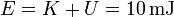
$E = K + U = 10\,\mathrm{mJ}$

Para una altura intermedia las expresiones de las diferentes energías son

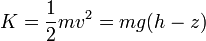
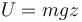
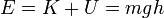
$K = \frac{1}{2}mv^2 = mg(h-z)$ $U=mgz\,$ $E=K+U = mgh\,$

4 Ecuación diferencial

Una partícula pequeña que se mueve en un fluido viscoso, como el aire, experimenta una fuerza de rozamiento que, para pequeñas celeridades, es proporcional a la velocidad y opuesta a ella

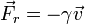
$\vec{F}_r=-\gamma\vec{v}$

de forma que el movimiento de una gota de lluvia verifica la ecuación de movimiento

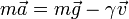
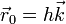
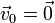
$m\vec{a}=m\vec{g}-\gamma\vec{v}$ $\vec{r}_0=h\vec{k}$ $\vec{v}_0=\vec{0}$

Puesto que el movimiento es puramente vertical, podemos reducir el problema al estudio de la componente Z y escribir todos los vectores como

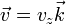
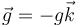
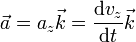
$\vec{v}=v_z\vec{k}$ $\vec{g}=-g\vec{k}$ $\vec{a}=a_z\vec{k}=\frac{\mathrm{d}v_z}{\mathrm{d}t}\vec{k}$

Tenemos entonces la ecuación de movimiento

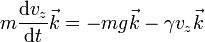
$m\frac{\mathrm{d}v_{z}}{\mathrm{d}t}\vec{k}=-mg\vec{k}-\gamma v_{z}\vec{k}$

Puesto que dos vectores son iguales cuando lo son sus componentes, podemos igualar la componente Z y reducir el problema a la ecuación escalar

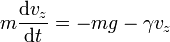
$m\frac{\mathrm{d}v_{z}}{\mathrm{d}t}=-mg-\gamma v_{z}$

Nótese que en esta ecuación no se ha hecho ninguna hipótesis sobre el sentido de la velocidad, sólo sobre su dirección. La componente $v z$ puede ser un número negativo (de hecho lo será, pues la partícula está cayendo), en cuyo caso la fuerza de rozamiento irá hacia arriba. El que aparezca un signo menos delante de la fuerza de rozamiento no implica que el sentido sea hacia abajo.

5 Velocidad límite

Antes de dar la solución, veamos cómo es el movimiento. Inicialmente la velocidad es nula, por lo que no hay fricción. El movimiento comienza siendo prácticamente uniformemente acelerado. Sin embargo, a medida que la celeridad va aumentando, la fricción crece y la aceleración disminuye. Llega un momento en que la fuerza de rozamiento iguala al peso, y la velocidad deja de aumentar en módulo, permaneciendo en su valor límite, dado por

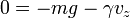
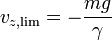
$0 = -mg -\gamma v_{z}\,$ $\Rightarrow$ $v_{z,\mathrm{lim}} = -\frac{mg}{\gamma}$

es negativa, pues se dirige hacia abajo.

Su valor numérico lo obtenemos hallando en primer lugar el valor de \gamma para esta gota de lluvia. Sustituyendo R = 0.50 mm

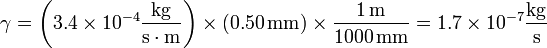
$\gamma = \left(3.4\times 10^{-4} \frac{\mathrm{kg}}{\mathrm{s}\cdot\mathrm{m}}\right)\times(0.50\,\mathrm{mm})\times\frac{1\,\mathrm{m}}{1000\,\mathrm{mm}}=1.7\times 10^{-7}\frac{\mathrm{kg}}{\mathrm{s}}$

lo que nos da la celeridad límite

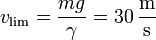
$v_\mathrm{lim} = \frac{mg}{\gamma}= 30\,\frac{\mathrm{m}}{\mathrm{s}}$

Esta velocidad ya es considerablemente inferior a la que habíamos obtenido suponiendo despreciable el rozamiento. Aun así, es considerablemente mayor que el valor experimental que se tiene para las gotas de lluvia, que puede rondar los 10 m/s. La diferencia se debe a que el rozamiento es realmente más intenso y requiere fórmulas más complicadas.

6 Caída a la velocidad límite

Si la altura de caída es muy grande, puede suponerse que la velocidad es prácticamente la límite para todo el trayecto, con lo que la celeridad de impacto es la celeridad límite

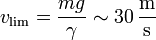
$v_\mathrm{lim} = \frac{mg}{\gamma}\sim 30\,\frac{\mathrm{m}}{\mathrm{s}}$

y el tiempo de caída es aproximadamente

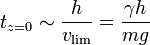
$t_{z=0}\sim \frac{h}{v_\mathrm{lim}} = \frac{\gamma h}{mg}$

Este resultado sí está de acuerdo con la experiencia cotidiana de que los objetos más pesados tardan menos en caer e impactan con una mayor celeridad. Para una gota de agua de 0.50 mm de radio predice un tiempo de caída de 67 s y una celeridad de impacto de 30 m/s, valor mucho más razonable que el que omite el rozamiento. La energía mecánica de la gota al llegar al suelo es exclusivamente la energía cinética asociada a la celeridad límite, la cual evaluada para los datos numéricos del enunciado resulta ser de 0.2 mJ, que comparados con los 10 mJ de energía mecánica inicial revelan el hecho de que la práctica totalidad de la energía mecánica (en concreto, 9.8 mJ) se ha visto disipada durante la caída por causa de la fuerza de fricción viscosa.

7 Velocidad y posición con rozamiento

La solución exacta la obtenemos hallando el incremento de velocidad entre dos instantes sucesivos

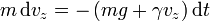
$m\,\mathrm{d}v_{z} = -\left(mg+\gamma v_{z}\right)\mathrm{d}t$

Despejando obtenemos el tiempo que tarda en producirse un aumento de velocidad diferencial como

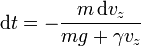
$\mathrm{d}t = -\frac{m\,\mathrm{d}v_{z}}{mg+\gamma v_{z}}$

Sumando todos los incrementos

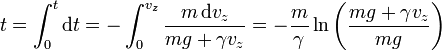
$t = \int_0^t\mathrm{d}t = -\int_0^{v_{z}} \frac{m\,\mathrm{d}v_{z}}{mg+\gamma v_{z}} = -\frac{m}{\gamma}\ln\left(\frac{mg+\gamma v_{z}}{mg}\right)$

Despejando la velocidad como función del tiempo

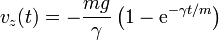
$v_{z}(t) = -\frac{mg}{\gamma}\left(1-\mathrm{e}^{-\gamma t/m}\right)$

El comportamiento de esta función predice que efectivamente la velocidad tiende hacia la velocidad límite. Integrando de nuevo obtenemos la altura como función del tiempo

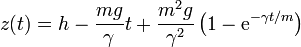
$z(t) = h-\frac{mg}{\gamma}t+\frac{m^2g}{\gamma^2}\left(1-\mathrm{e}^{-\gamma t/m}\right)$

Sin embargo, para hallar el instante exacto en que llega al suelo ( $t z = 0$ ) es preciso resolver una ecuación que solo admite solución numérica.

Caída libre de un cuerpo

De Laplace

Contenido

1 Enunciado

2 Tiempo y velocidad sin rozamiento

3 Energía sin rozamiento

4 Ecuación diferencial

5 Velocidad límite

6 Caída a la velocidad límite

7 Velocidad y posición con rozamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES