Problemas de corriente eléctrica
De Laplace
| Línea 47: | Línea 47: | ||
<center><math>\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ | <center><math>\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ | ||
r_2 \mathrm{e}^{-\alpha_2 z}+r_3 \mathrm{e}^{-\alpha_3 z} | r_2 \mathrm{e}^{-\alpha_2 z}+r_3 \mathrm{e}^{-\alpha_3 z} | ||
| - | </math></center> | + | </math></center> |
| + | |||
donde | donde | ||
Revisión de 09:29 5 jun 2008
Contenido |
1 Flujo de líquido por una tubería
Por el interior de una tubería cilíndrica de radio a fluye un líquido con una velocidad, dependiente de la distancia al eje, ρ, como
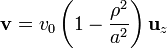
El líquido posee una densidad de carga uniforme ρ0, de forma que la densidad de corriente es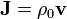 
. En el exterior del tubo no hay corriente.
- Calcule la intensidad de corriente que atraviesa una sección por la tubería.
- Si se desea que por la superficie del tubo circule una corriente superficial
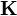, de forma que la corriente total sea nula, ¿cuánto debe valer ?
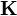2 Velocidad de arrastre
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
3 Nube de carga en expansión
Una nube esférica de carga (compuesta de una distribución de cargas puntuales flotando en el vacío) se encuentra en expansión, creciendo el radio de la esfera como R(t) = R0 + vt. La carga total de la nube, Q0, se encuentra distribuida en todo momento de forma uniforme en el volumen de la esfera.
A partir de la ley de conservación de la carga, calcule la densidad de corriente de conducción en la nube. Puede suponer que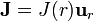 
y que esta densidad no es infinita en el centro de la esfera.
Calcule el campo eléctrico en los puntos del espacio y, a partir de éste, la corriente de desplazamiento. ¿Cuánto vale la densidad de corriente total?
¿Habrá campo magnético en el sistema?
4 Resistencia de un tubo
Sea un tubo cilíndrico, de radio interior a y exterior b, y longitud h, de un material de conductividad σ. Calcule la resistencia eléctrica
- Entre las dos bases.
- Entre la cara interior y la exterior.
5 Cable bimetálico
Entre los distintos tipos de cable empleados en la industria, se encuentra el de aluminio revestido de cobre. Está formado por un núcleo de aluminio de radio a (suponga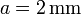 
), rodeado por una capa de cobre, de radio exterior b (sea 
).
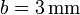- Calcule la resistencia de cable de esta clase de longitud
.
- Determine la corriente que circula por cada metal cuando se aplica una diferencia de potencial
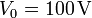al cable anterior.
6 Conductividad del suelo
Para determinar la conductividad σ del suelo se mide la corriente entre dos electrodos clavados en tierra y sometidos a una cierta diferencia de potencial.
- Suponga en primer lugar sólo un electrodo hemisférico de radio a, perfectamente conductor, puesto a un potencial V1 respecto a puntos muy alejados. En el estado estacionario, determínese la distribución de potencial en el suelo. Admita que el potencial depende exclusivamente de la distancia al centro del electrodo. A partir de este resultado, calcule la resistencia entre el electrodo y el infinito. Suponga que el suelo posee conductividad igual en todos sus puntos.
- Suponga ahora dos electrodos del tipo anterior, del mismo radio, y muy alejados entre sí. Si se conectan por el aire mediante un cable ideal y una fuente de continua de tensión V0, ¿qué corriente circula de un electrodo al otro?
- Si para una tensión de
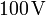entre dos electrodos de 
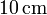de radio se mide una corriente de 
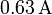, ¿cuánto vale la conductividad del suelo?
7 Corrientes atmosféricas
La resistividad del aire en la atmósfera decrece exponencialmente con la altura como
donde
El campo eléctrico en zonas despejadas de la superficie de la Tierra vale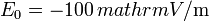 
. Este campo es prácticamente constante y va siempre en la dirección vertical.
A partir de estos datos halle
- El valor del campo eléctrico para un punto situado entre la superficie de la Tierra y la ionosfera (
).
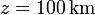- La diferencia de potencial entre la superficie y la ionosfera.
- La distribución de cargas en la atmósfera.
- La corriente total que llega a la superficie de la Tierra.
- La potencia necesaria para mantener esta corriente estacionaria
- Estime el tiempo que tardaría la atmósfera en descargarse si no existiera un mecanismo generador
