Coordenadas cartesianas. Definición
De Laplace
(Nueva página: rightEl sistema de coordenadas cartesianas <math>(x,y,z)\,</math> es el que tomaremos como sistema básico. Este sistema se define como el conjunto de distanci...) |
(→La mosca y el señor Descartes) |
||
| (14 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | <categorytree mode=pages depth="0" style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;">Sistemas de coordenadas</categorytree> | ||
| + | |||
| + | <categorytree mode=pages depth="0" style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;">Coordenadas cartesianas</categorytree> | ||
| + | |||
| + | <categorytree mode=pages depth="0" style="float:right; clear:right; margin-left:1ex; border:1px solid gray; padding:0.7ex; background-color:white;">Definición de sistemas</categorytree> | ||
| + | |||
| + | ==Definición== | ||
[[Imagen:car-def.png|right]]El sistema de coordenadas cartesianas <math>(x,y,z)\,</math> es el que tomaremos | [[Imagen:car-def.png|right]]El sistema de coordenadas cartesianas <math>(x,y,z)\,</math> es el que tomaremos | ||
| Línea 12: | Línea 19: | ||
el punto. Las tres coordenadas varían en el mismo rango: | el punto. Las tres coordenadas varían en el mismo rango: | ||
| - | <math>x\in (-\infty,+\infty)\qquad y\in (-\infty,+\infty)\qquad z\in (-\infty,+\infty)</math> | + | <center><math>x\in (-\infty,+\infty)\qquad y\in (-\infty,+\infty)\qquad z\in (-\infty,+\infty)</math></center> |
En términos de las coordenadas cartesianas, el vector de posición se | En términos de las coordenadas cartesianas, el vector de posición se | ||
escribe como | escribe como | ||
| - | <math>\mathbf{r} = x\mathbf{i}+y\mathbf{j}+z\mathbf{k}</math> | + | <center><math>\mathbf{r} = x\mathbf{i}+y\mathbf{j}+z\mathbf{k}</math></center> |
| Línea 23: | Línea 30: | ||
La invención de las coordenadas cartesianas se debe a René Descartes (o | La invención de las coordenadas cartesianas se debe a René Descartes (o | ||
| - | + | ''Cartesius'', del cual toman el nombre). Según parece, | |
encontrándose en la cama con gripe, fue incordiado por una ruidosa | encontrándose en la cama con gripe, fue incordiado por una ruidosa | ||
mosca. Dentro de su estado febril, a Descartes se le ocurrió que si se | mosca. Dentro de su estado febril, a Descartes se le ocurrió que si se | ||
| Línea 37: | Línea 44: | ||
===¿Donde se usan las coordenadas cartesianas?=== | ===¿Donde se usan las coordenadas cartesianas?=== | ||
| - | En todas partes. Por poner un ejemplo de la vida diaria, podemos pensar | + | En todas partes. Por poner un ejemplo de la vida diaria, podemos pensar en la ubicación de los productos en un hipermercado, identificados por una calle (<math>x</math>), una profundidad en la calle (<math>y</math>) y una altura de estante (<math>z</math>). |
| - | en la ubicación de los productos en un hipermercado, identificados por | + | |
| - | una calle ( | + | ==Enlaces== |
| - | estante ( | + | * '''Siguiente:''' [[Coordenadas cilíndricas. Definición]] |
| + | * '''Anterior:''' [[Definición de sistemas de coordenadas]] | ||
| + | * [[Coordenadas cartesianas. Líneas y superficies coordenadas]] | ||
| + | * [[Coordenadas cartesianas. Base vectorial]] | ||
| + | |||
| + | [[Categoría:Coordenadas cartesianas|10]] | ||
| + | [[Categoría:Definición de sistemas|20]] | ||
última version al 18:22 13 abr 2010
Contenido |
1 Definición
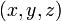es el que tomaremos
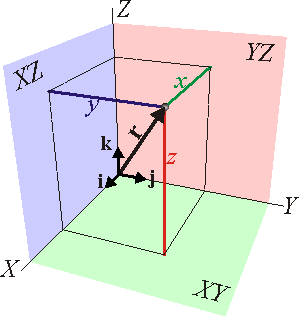
como sistema básico. Este sistema se define como el conjunto de distancias (con signo) a tres planos ortogonales.
- La coordenada x es la distancia al plano YZ.
- La coordenada y es la distancia al plano XZ.
- La coordenada z es la distancia al plano XY.
El signo en estas coordenadas indica a qué lado del plano se encuentra el punto. Las tres coordenadas varían en el mismo rango:
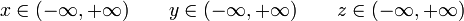
En términos de las coordenadas cartesianas, el vector de posición se escribe como
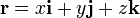
1.1 La mosca y el señor Descartes
La invención de las coordenadas cartesianas se debe a René Descartes (o Cartesius, del cual toman el nombre). Según parece, encontrándose en la cama con gripe, fue incordiado por una ruidosa mosca. Dentro de su estado febril, a Descartes se le ocurrió que si se anotaba la distancia a las paredes y al suelo, podría describirse la posición de la mosca como función del tiempo.
Esta invención, que podría parecer trivial, fue absolutamente revolucionaria, ya que permitió pasar de la geometría sintética (basada en figuras y en la que los puntos eran identificados por letras) a la geometría analítica en la que los entes geométricos y los teoremas son expresados mediante fórmulas y relaciones numéricas.
1.2 ¿Donde se usan las coordenadas cartesianas?
En todas partes. Por poner un ejemplo de la vida diaria, podemos pensar en la ubicación de los productos en un hipermercado, identificados por una calle (x), una profundidad en la calle (y) y una altura de estante (z).
