Potencial eléctrico debido a una polarización

De Laplace

(Diferencias entre revisiones)

última version al 19:48 14 feb 2010

El potencial eléctrico debido a una polarización es la suma de los potenciales debidos a cada dipolo.

El potencial de un solo dipolo situado en el origen de coordenadas es

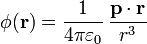
$\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\,\frac{\mathbf{p}\cdot\mathbf{r}}{r^3}$

Si en lugar de encontrarse en el origen se encuentra en un punto $\mathbf{r}_0$ empleamos la posición relativa a este punto

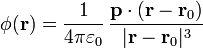
$\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\,\frac{\mathbf{p}\cdot(\mathbf{r}-\mathbf{r}_0)}{|\mathbf{r}-\mathbf{r}_0|^3}$

Si ahora consideramos un conjunto de dipolos situados en posiciones 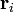$\mathbf{r}_i$ el potencial eléctrico total será la suma de los potenciales individuales

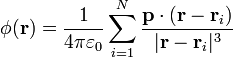
$\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N\frac{\mathbf{p}\cdot(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}$

Cuando el número de dipolos es muy grande, la suma se puede aproximar por una integral. Para ello, dividimos el volumen total polarizado en elementos de volumen $Δτ'$ y aplicamos que, según la definición de polarización de un medio material

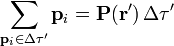
$\sum_{\mathbf{p}_i\in\Delta\tau'}\mathbf{p}_i = \mathbf{P}(\mathbf{r}')\,\Delta\tau'$

con lo que queda

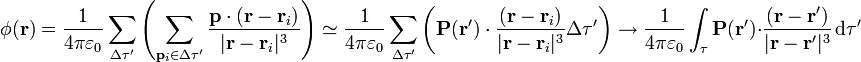
$\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{\Delta\tau'}\left(\sum_{\mathbf{p}_i\in\Delta\tau'}\frac{\mathbf{p}\cdot(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}\right)\simeq \frac{1}{4\pi\varepsilon_0}\sum_{\Delta\tau'}\left(\mathbf{P}(\mathbf{r}')\cdot\frac{(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}\Delta\tau'\right) \to \frac{1}{4\pi\varepsilon_0}\int_\tau \mathbf{P}(\mathbf{r}'){\cdot}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau'$

Esta integral suele ser difícil de calcular por métodos analíticos. Uno de los pocos ejemplos en los que es factible es el de una esfera polarizada uniformemente.

@@ Línea 13: / Línea 13: @@
 <center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N\frac{\mathbf{p}\cdot(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}</math></center>
-Cuando el número de dipolos es muy grande, la suma se puede aproximar por una integral. Para ello, dividimos el volumen total polarizado en elementos de volumen <math>\Delta\tau'</math> y aplicamos que, según la definición de [[polarización en un material]]
+Cuando el número de dipolos es muy grande, la suma se puede aproximar por una integral. Para ello, dividimos el volumen total polarizado en elementos de volumen <math>\Delta\tau'</math> y aplicamos que, según la definición de [[polarización de un medio material]]
 <center><math>\sum_{\mathbf{p}_i\in\Delta\tau'}\mathbf{p}_i = \mathbf{P}(\mathbf{r}')\,\Delta\tau'</math></center>
@@ Línea 22: / Línea 22: @@
 </math></center>
-Esta integral suele ser difícil de calcular por métodos analíticos.
+Esta integral suele ser difícil de calcular por métodos analíticos. Uno de los pocos ejemplos en los que es factible es el de una [[esfera polarizada uniformemente]].
-Una descripción alternativa es mediante las ''[[densidades de carga de polarización]]'' o de ''carga ligada'', definidas como
-<center><math>\rho_p = -\nabla{\cdot}\mathbf{P}</math>{{qquad}}{{qquad}}<math>\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]\,</math></center>
-La última fórmula, con el salto en la polarización, se aplica a una interfaz entre dos dieléctricos. Si uno de ellos es el vacío (en el
-cual <math>\mathbf{P}=\mathbf{0}</math>), esta expresión se reduce a <math>\sigma_p = \mathbf{P}{\cdot}\mathbf{n}</math>. En términos de <math>\rho_p</math> y <math>\sigma_p</math> el potencial es
-<center><math>\phi = \frac{1}{4\pi\varepsilon_0}\int_\tau\frac{\rho_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+
-\frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'</math></center>
-Empleando las cargas de polarización, las ecuaciones de la electrostática en presencia de dieléctricos se escriben como
-<center><math>\nabla{\cdot}\mathbf{E} = \frac{\rho_l+\rho_p}{\varepsilon_0}</math>{{qquad}}{{qquad}}<math>\nabla\times \mathbf{E} =\mathbf{0}</math></center>
-con las condiciones de salto
-<center><math>\mathbf{n}{\cdot}[\mathbf{E}] = \frac{\sigma_l+\sigma_p}{\varepsilon_0}</math>{{qquad}}{{qquad}}<math>\mathbf{n}\times
-[\mathbf{E}]=\mathbf{0}</math></center>
-siendo <math>\rho_l</math> y <math>\sigma_l</math> las ''densidades de carga libre'', definidas como aquellas que no son de polarización.
 [[Categoría:Comportamiento dieléctrico de la materia]]

Potencial eléctrico debido a una polarización

De Laplace

última version al 19:48 14 feb 2010

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES