Entrar Página Discusión Historial Go to the site toolbox

Test del Examen Parcial 2013-2014

De Laplace

Contenido

1 Posible máquina térmica

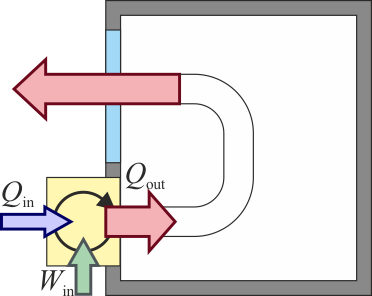
Una supuesta máquina térmica extrae 500 MW de un foco a 1200 K y produce 200 MW de calor de desecho que expulsa al ambiente a 300 K. ¿Qué podemos decir de esta máquina?

  • A Es posible y tiene un rendimiento del 75%
  • B Es posible y tiene un rendimiento del 40%
  • C Esta máquina es imposible.
  • D Es posible y tiene un rendimiento del 60%

1.1 Solución

La respuesta correcta es la D.

De acuerdo con los datos de la pregunta

\dot{Q}_\mathrm{in}=500\,\mathrm{MW}\qquad\qquad\dot{Q}_\mathrm{out}=200\,\mathrm{MW}

lo que da un posible rendimiento

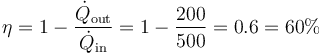
\eta = 1-\frac{\dot{Q}_\mathrm{out}}{\dot{Q}_\mathrm{in}}=1-\frac{200}{500}=0.6=60\%

Tenemos que ver si esta máquina es posible. El máximo rendimiento lo da una máquina reversible que opere entre las temperaturas extremas

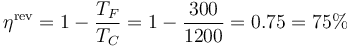
\eta^\mathrm{rev}=1-\frac{T_F}{T_C}=1-\frac{300}{1200}=0.75=75\%

Puesto que el rendimiento propuesto es menor que el máximo, la máquina es posible y su rendimiento es el 60%.

2 Principio del motor diésel

¿Por qué un motor diésel puede alcanzar una relación de compresión más alta que uno de gasolina, que sigue el ciclo Otto?

  • A Eso es falso. La mayor relación de compresión la alcanzan los motores de gasolina.
  • B Porque los motores diésel trabajan a una temperatura más baja que los de gasolina.
  • C Porque el diésel comprime solamente aire.
  • D Porque el diésel emplea gasoil como combustible.

2.1 Solución

La respuesta correcta es la C.

Tal como se explica en el artículo general correspondiente a las Máquinas térmicas y en el específico sobre el Ciclo Diesel, la ventaja del motor diésel es que comprime solamente aire, inyectándose el combustible una vez que el pistón está cerca del punto muerto superior (PMS). Al comprimir solo aire, la relación de compresión (cociente entre el volumen en el PMI y en el PMS) puede ser muy alta, ya que no hay peligro de que explote.

3 Dilatación de una arandela

Una arandela de acero tiene a 20°C un radio interior de 4 mm y uno exterior de 8 mm. El coeficiente de dilatación lineal del acero es 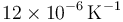12\times 10^{-6}\,\mathrm{K}^{-1} Cuando la arandela se calienta hasta 100°C. ¿Cuánto varía el radio del agujero?

  • A Disminuye en 4 μm
  • B Disminuye en 2 μm
  • C Aumenta en 2 μm.
  • D Aumenta en 4 μm.

3.1 Solución

La respuesta correcta es la D.

La fórmula para la dilatación lineal de un sólido es

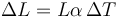
\Delta L = L \alpha\,\Delta T

Aplicándola al caso del radio queda

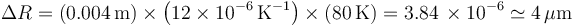
\Delta R = (0.004\,\mathrm{m})\times\left(12\times 10^{-6}\,\mathrm{K}^{-1}\right)\times(80\,\mathrm{K})=3.84\,\times 10^{-6}\simeq 4\,\mu\mathrm{m}

Luego el radio del agujero aumenta en 4 micras.

4 Afirmación sobre el primer principio

¿Cuál de las siguientes afirmaciones es cierta?

  • A En todo proceso cíclico de un sistema, el trabajo neto que entra es nulo.
  • B En todo proceso cíclico de un sistema, el calor neto que entra es nulo.
  • C Para todo sistema, la suma del calor y del trabajo netos que entran es independiente del proceso entre dos estados dados.
  • D En todo proceso de un sistema el calor neto que entra es igual al trabajo neto que sale de él.

4.1 Solución

La respuesta correcta es la C.

La respuesta C es simplemente el enunciado del Primer Principio de la Termodinámica.

Si la respuesta A o B fueran ciertas, no podrían existir las máquinas o los refrigeradores, mientras que si fuera cierta la D nunca podría cambiar la temperatura de nada, ya que la energía interna sería siempre constante.

5 Diagrama pV del agua

La gráfica representa una isoterma en las proximidades de un cambio de fase de agua a vapor, en un diagrama pV.

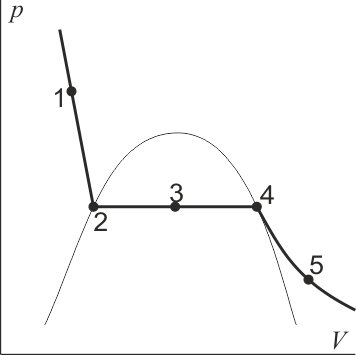
Archivo:saturacion.png

En el estado etiquetado como “2” tenemos

  • A Líquido saturado
  • B Vapor saturado
  • C Vapor sobrecalentado
  • D Líquido subenfriado

5.1 Solución

La respuesta correcta es la A.

A medida que vamos pasando de agua líquida a vapor de agua el volumen que ocupa aumenta. por tanto, en la gráfica el agua queda a la izquierda y el vapor de agua a la derecha.

Tal como se describe en el artículo sobre propiedades del agua, en el estado 1 tenemos agua a mayor presión que la de saturación o a menor temperatura que la correspondiente a la de saturación a esa presión. Por eso se dice que tenemos en 1 líquido comprimido o líquido subenfriado.

Cuando se aumenta el volumen se alcanza la saturación, en la que el agua está en equilibrio térmico con su vapor. En 2 tenemos agua saturada (justo a punto de entrar en ebullición), en 3 tenemos mezcla saturada de agua y vapor y 4 todo el agua se ha transformado en vapor, con lo que tenemos vapor saturado.

Si seguimos aumentando el volumen, en el estado 5 tenemos vapor sobrecalentado, es decir, vapor de agua a una temperatura superior a la de ebullición o saturación a esa presión.

Por tanto, en el 2, lo que hay es líquido saturado.

6 Calentamiento de una habitación

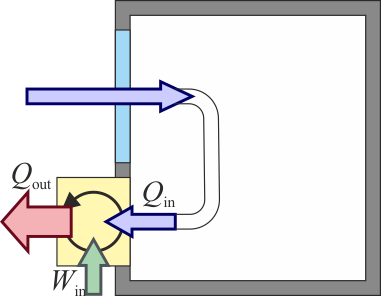
Una habitación de encuentra a 22°C y el exterior a 2°C. Si las paredes tienen una resistencia térmica de 8 mK/W y para mantener constante la temperatura de la habitación se usa una bomba de calor, cuál es el flujo de trabajo (potencia) mínimo que hay que consumir para mantener la habitación caldeada?

6.1 Pregunta 1

  • A 169 W
  • B 37 MW
  • C 2500 W
  • D 2270 W

6.1.1 Solución

La respuesta correcta es la A.

Tenemos aquí dos cálculos. Por un lado hallar cuanto calor escapa de la habitación por conducción, y por otro cuanto trabajo hace falta para reponer ese calor.

El flujo de calor hacia el exterior lo da la ley de Fourier

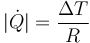
|\dot{Q}| = \frac{\Delta T}{R}

que en este caso da

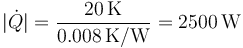
|\dot{Q}| = \frac{20\,\mathrm{K}}{0.008\,\mathrm{K}/\mathrm{W}}=2500\,\mathrm{W}

Este es el calor que escapa y que hay que reponer, pero no es esto lo que se pide. Hay que hallar la potencia mínima necesaria para reponerlo. Ésta la da una bomba de calor reversible que opere entre las dos temperaturas

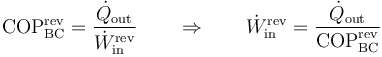
\mathrm{COP}_\mathrm{BC}^\mathrm{rev}=\frac{\dot{Q}_\mathrm{out}}{\dot{W}^\mathrm{rev}_\mathrm{in}}\qquad\Rightarrow\qquad \dot{W}^\mathrm{rev}_\mathrm{in} = \frac{\dot{Q}_\mathrm{out}}{\mathrm{COP}_\mathrm{BC}^\mathrm{rev}}

siendo el coeficiente de desempeño máximo

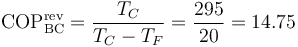
\mathrm{COP}_\mathrm{BC}^\mathrm{rev}=\frac{T_C}{T_C-T_F}=\frac{295}{20}=14.75

y la potencia mínima

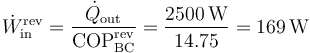
\dot{W}^\mathrm{rev}_\mathrm{in} = \frac{\dot{Q}_\mathrm{out}}{\mathrm{COP}_\mathrm{BC}^\mathrm{rev}}=\frac{2500\,\mathrm{W}}{14.75}=169\,\mathrm{W}

6.2 Pregunta 2

Supongamos que se eleva la temperatura de la habitación a 25°C. ¿Cuánto aumenta aproximadamente la potencia mínima necesaria?

  • A Un 15%.
  • B Un 1%.
  • C Un 30%
  • D Un 12%

6.2.1 Solución

La respuesta correcta es la B.

Cuando cambiamos la diferencia de temperaturas se modifican dos factores:

  • Escapa más calor de la habitación
  • Disminuye el coeficiente de desempeño de la bomba de calor

Repitiendo los cálculos de la pregunta anterior obtenemos, para el nuevo flujo de calor

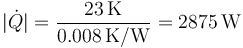
|\dot{Q}| = \frac{23\,\mathrm{K}}{0.008\,\mathrm{K}/\mathrm{W}}=2875\,\mathrm{W}

y para el nuevo coeficiente de desempeño

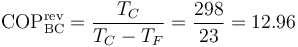
\mathrm{COP}_\mathrm{BC}^\mathrm{rev}=\frac{T_C}{T_C-T_F}=\frac{298}{23}=12.96

lo que da la nueva potencia mínima

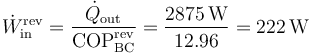
\dot{W}^\mathrm{rev}_\mathrm{in} = \frac{\dot{Q}_\mathrm{out}}{\mathrm{COP}_\mathrm{BC}^\mathrm{rev}}=\frac{2875\,\mathrm{W}}{12.96}=222\,\mathrm{W}

En proporción, comparando la nueva potencia mínima con la de la pregunta anterior

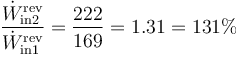
\frac{\dot{W}^\mathrm{rev}_\mathrm{in2}}{\dot{W}^\mathrm{rev}_\mathrm{in1}}=\frac{222}{169}=1.31 = 131\%

lo que supone un incremento en torno a un 30%. Vemos como una subida aparentemente pequeña en la temperatura interior supone un gran aumento en el consumo.

7 Producción de entropía en un frigorífico

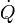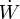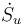El interior de un frigorífico se mantiene a una temperatura constante TF, estando el exterior a TC. Por conducción, hay un flujo de calor hacia el interior de valor \dot{Q}. El frigorífico, para extraer este calor, consume una potencia \dot{W}. ¿Cuánto aumenta la entropía del universo por segundo, \dot{S}_u?

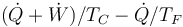
  • A (\dot{Q}+\dot{W})/T_C-\dot{Q}/T_F
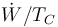
  • B \dot{W}/T_C
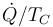
  • C \dot{Q}/T_C
  • D \dot{Q}/T_F-\dot{Q}/T_C

7.1 Solución

La respuesta correcta es la B.

Tenemos aquí dos procesos simultáneos:

  • La producción de entropía por el flujo de calor por conducción
  • La producción de entropía por el refrigerador

El total será la suma de ambos.

El primer término supone un aumento de la entropía del interior, donde se vierte calor, y una disminución del exterior, de donde se extrae. La cantidad de calor extraída y cedida es la misma:

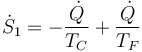
\dot{S}_1 = -\frac{\dot{Q}}{T_C}+\frac{\dot{Q}}{T_F}

Para el refrigerador el principio es el mismo, ahora tenemos calor extraído del interior y calor expulsado al exterior, con la diferencia de que el calor expulsado es ahora mayor que el extraído, ya que hay que contar el trabajo que se convierte en calor

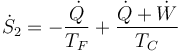
\dot{S}_2 = -\frac{\dot{Q}}{T_F}+\frac{\dot{Q}+\dot{W}}{T_C}

Sumando las dos contribuciones

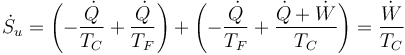
\dot{S}_u=\left(-\frac{\dot{Q}}{T_C}+\frac{\dot{Q}}{T_F}\right)+\left(-\frac{\dot{Q}}{T_F}+\frac{\dot{Q}+\dot{W}}{T_C}\right)=\frac{\dot{W}}{T_C}

El resultado neto es que la producción de entropía debida a la transferencia de calor de ida y vuelta se cancela, y solo queda la producción debida al trabajo extra que se convierte en calor.

Obtenido de "http://tesla.us.es/wiki/index.php/Test_del_Examen_Parcial_2013-2014"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 10:55, 8 abr 2014. - Esta página ha sido visitada 9.510 veces. - Aviso legal - Acerca de Laplace