Test de la tercera convocatoria de Física I 2013-2014 (GIE)

De Laplace

1 Movimiento de una L

Las velocidades de los extremos de una barra en L que describe un movimiento plano son las representadas en la figura, donde la cuadrícula está medida en m para las distancias y en m/s para las velocidades

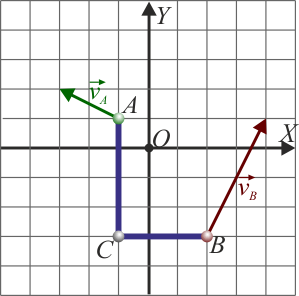
1.1 Pregunta 1

¿Dónde se encuentra el centro instantáneo de rotación (CIR)?

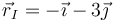
A $\vec{r}_I=-\vec{\imath}-3\vec{\jmath}$
B $\vec{r}_I=-2\vec{\imath}-\vec{\jmath}$
C $\vec{r}_I=\vec{0}$
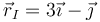
D $\vec{r}_I=3\vec{\imath}-\vec{\jmath}$

1.1.1 Solución

La respuesta correcta es la B.

En un movimiento plano, el CIR se encuentra en la intersección de las perpendiculares por cada punto a la velocidad de dicho punto. Trazando sendas perpendiculares por A y por B a las velocidades respectivas obtenemos que el punto de corte es el (−2,−1).

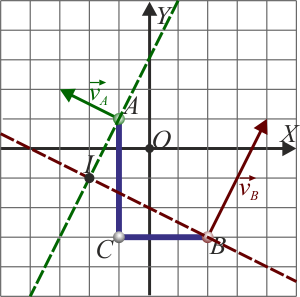
1.2 Pregunta 2

¿Cuál es la velocidad del vértice C?

A No hay información suficiente para calcularla
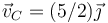
B $\vec{v}_C=(5/2)\vec{\jmath}$
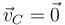
C $\vec{v}_C=\vec{0}$
D $\vec{v}_C=2\vec{\imath}+\vec{\jmath}$

1.2.1 Solución

La respuesta correcta es la D.

Una vez que tenemos localizado el CIR sabemos que para cualquier otro punto, la velocidad se encuentra en la perpendicular a la recta que pasa por el CIR y por él. De las cuatro soluciones, hay solo una que cumple esta ortogonalidad, lo que descarta la opción B.

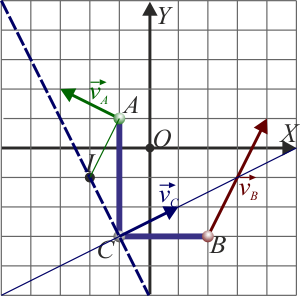
Ahora, el punto C no coincide con el CIR, luego su velocidad no es nula. Esto descarta la opción C.

Por otra parte, a igualdad de distancia al eje, misma rapidez. C está a la misma distancia de I que el vértice A, luego tiene la misma rapidez que éste. Queda el sentido de la velocidad, que lo da la regla de la mano derecha. La respuesta que cumple todas estas condiciones es la D.

También puede calcularse sin necesidad de emplear métodos gráficos.

Por la condición de rigidez se cumple que

$\vec{v}_C\cdot\overrightarrow{CA}=\vec{v}_A\cdot\overrightarrow{CA}\qquad\qquad \vec{v}_C\cdot\overrightarrow{CB}=\vec{v}_B\cdot\overrightarrow{CB}$

siendo

$\vec{v}_A=-2\vec{\imath}+\vec{\jmath}\qquad\vec{v}_B=2\vec{\imath}+4\vec{\jmath}\qquad\qquad \vec{v}_C=v_x\vec{\imath}+v_y\vec{\jmath}$

y

$\overrightarrow{CA}=4\vec{\jmath}\qquad\overrightarrow{CB}=3\vec{\imath}$

por tanto

$\left\{\begin{array}{rcl}4v_y & = & 4\cdot 1\\ 3v_x & = & 3\cdot 2\end{array}\right. \qquad\Rightarrow\qquad \left\{\begin{array}{rcl}v_y & = & 1\\ v_x & = & 2\end{array}\right.\qquad\Rightarrow\qquad \vec{v}_C=2\vec{\imath}+\vec{k}$

2 Relación del ergio con el julio

El sistema cegesimal se basa en el centímetro como unidad de longitud, el gramo como unidad de masa y el segundo como unidad de tiempo. La unidad de energía en el sistema cegesimal es el ergio, combinación de las básicas. ¿A cuantos julios equivale un ergio?

A $10 - 5$
B $10 - 4$
C $10 - 3$
D $10 - 7$

2.1 Solución

La respuesta correcta es la D.

Las dimensiones de la energía son

$[E]=\frac{M\cdot L^2}{T^2}$

por tanto, un ergio y un julio son iguales a

$1\,\mathrm{erg}=1\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}\qquad\qquad 1\,\mathrm{J}=1\,\frac{,\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}^2}$

aplicando los factores de conversión

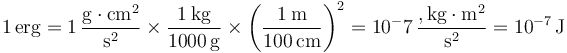
$1\,\mathrm{erg}=1\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}\times \frac{1\,\mathrm{kg}}{1000\,\mathrm{g}}\times\left(\frac{1\,\mathrm{m}}{100\,\mathrm{cm}}\right)^2 = 10^-7\,\frac{,\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}^2}=10^{-7}\,\mathrm{J}$

3 Partícula sometida a dos fuerzas

Una partícula de 1 kg está sometida a dos fuerzas constantes de 10 N, que forman un ángulo de 120°. La aceleración de esta partícula, en módulo, es igual a…

A 20 m/s²
B 0 m/s²
C 10 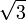$\sqrt{3}$ m/s²
D 10 m/s²

3.1 Solución

La respuesta correcta es la D.

Es una consecuencia de la suma de vectores.

para este caso particular, la fuerza resultante tiene el mismo módulo que las dos que se suman. Puesto que la masa es 1 kg, resulta la aceleración de la respuesta D.

4 Partícula sometida a un potencial

Una partícula describe un movimiento rectilíneo sometida a una fuerza 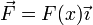$\vec{F}=F(x)\vec{\imath}$ cuya energía potencial vale

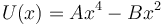
$U(x) = Ax^4-Bx^2\,$

( $A$ y $B$ , constantes positivas)

4.1 Pregunta 1

¿Cuánto vale la fuerza sobre la partícula, $F (x)$ ?

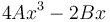
A $-4Ax^3+2Bx\,$
B $(4Ax^3-2Bx)v\,$
C 0
D $4Ax^3-2Bx\,$

4.1.1 Solución

La respuesta correcta es la A.

Dada una fuerza conservativa, el valor de esta puede hallarse a partir de su energía potencial mediante el gradiente cambiado de signo. En el caso de que dependa de una sola variable, el cálculo se reduce a hallar

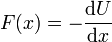
$F(x) = -\frac{\mathrm{d}U}{\mathrm{d}x}$

que en este caso da la respuesta A.

4.2 Pregunta 2

¿Qué tipo de punto es $x = 0$ para esta energía?

A De retorno.
B De equilibrio indiferente.
C De equilibrio estable.
D De equilibrio inestable.

4.2.1 Solución

La respuesta correcta es la D.

La primera derivada de la energía se anula en $x = 0$ .

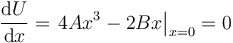
$\frac{\mathrm{d}U}{\mathrm{d}x}=\left. 4Ax^3 - 2Bx\right|_{x=0} = 0$

La segunda derivada es negativa en este punto

$\frac{\mathrm{d}^2U}{\mathrm{d}x^2}=\left.12Ax^2 - 2B\right|_{x=0} = -2B < 0$

Esto quiere decir que la energía potencial tiene un máximo en ese punto. Por tanto, se trata de un punto de equilibrio inestable.

5 Propiedad de un m.a.s.

En un movimiento armónico simple, cuando la elongación iguala a la amplitud…

A la velocidad y la aceleración son nulas.
B ni la velocidad ni la aceleración son nulas.
C la velocidad es nula, pero la aceleración no.
D la velocidad no es nula, pero la aceleración si.

5.1 Solución

La respuesta correcta es la C.

La amplitud de la oscilación es justamente la elongación máxima. Por tanto, cuando la elongación iguala a la amplitud alcanza su máximo alejamiento de la posición de equilibrio y a partir de ahí vuelve hacia atrás. Es ese instante de máximo alejamiento, la velocidad (derivada de la posición) es nula. La aceleración, sin embargo, no lo es, pues la velocidad está cambiando de positiva a negativa.

6 Ángulo entre velocidad y aceleración

La velocidad y la aceleración de una partícula forman, en un instante dado, un ángulo de $2π / 3$ . En ese instante la partícula…

A tiene una rapidez constante.
B está frenando.
C está aumentando su rapidez.
D tiene una rapidez máxima.

6.1 Solución

La respuesta correcta es la B.

La aceleración tangencial de una partícula es igual a

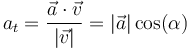
$a_t = \frac{\vec{a}\cdot\vec{v}}{|\vec{v}|}=|\vec{a}|\cos(\alpha)$

siendo α el ángulo que forman la velocidad y la aceleración. En este caso, al ser mayor de π/2, este coseno es negativo y

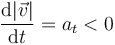
$\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=a_t < 0$

Como la rapidez está disminuyendo, la partícula está frenando.

7 Conservación en un sistema cerrado

En un sistema cerrado de partículas sometido exclusivamente a fuerzas internas newtonianas, ¿qué magnitud no se conserva en general?

A El momento cinético.
B La energía cinética.
C La masa.
D La cantidad de movimiento.

7.1 Solución

La respuesta correcta es la B.

En un sistema cerrado, las partículas que lo forman son siempre las mismas, por lo que la masa es constante.

Las fuerzas newtonianas entre un par de partículas son las que cumplen la tercera ley de Newton: son opuestas entre sí y además en la línea que une las dos partículas. Tal como se ve en el tema de sistemas de partículas,estas fuerzas conservan la cantidad de movimiento y el momento cinético. No conservan la energía cinética.

8 Movimiento con potencia constante

Una partícula se mueve en línea recta partiendo del reposo de forma que es constante la potencia que desarrolla la fuerza que actúa sobre ella. Para esta partícula, ¿cómo aumenta su rapidez con el tiempo?

A Permanece constante.
B Como $t$ .
C Como $t 2$ .
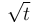D Como $\sqrt{{t}}$ .

8.1 Solución

La respuesta correcta es la D.

Por el teorema de las fuerzas vivas o del trabajo-energía cinética

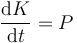
$\frac{\mathrm{d}K}{\mathrm{d}t}=P$

Si la potencia es constante, la energía cinética aumenta linealmente con el tiempo

$K = \overrightarrow{K_0}^{=0} +\int_0^ t P\,\mathrm{d}t=Pt$

y por tanto la rapidez aumenta como la raíz cuadrada del tiempo

$\frac{1}{2}m|\vec{v}|^2 = P t \qquad\Rightarrow\qquad |\vec{v}|=\sqrt{\frac{2P}{m}t}$

9 Movimiento en polares

Una partícula se mueve de forma que su posición se expresa en coordenadas polares como

$\rho = k t\qquad\qquad\varphi = \Omega t$

con $k$ y $Ω$ constantes positivas.

9.1 Pregunta 1

La velocidad de esta partícula es

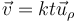
A $\vec{v}=kt\vec{u}_\rho$
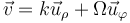
B $\vec{v}=k\vec{u}_\rho+\Omega\vec{u}_\varphi$
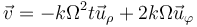
C $\vec{v}=-k\Omega^2 t\vec{u}_\rho+2k\Omega\vec{u}_\varphi$
D $\vec{v}=k\vec{u}_\rho+k\Omega t\vec{u}_\varphi$

9.1.1 Solución

La respuesta correcta es la D.

La velocidad de una partícula, en coordenadas polares, se expresa como

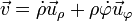
$\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\varphi}\vec{u}_\varphi$

siendo, en este caso,

$\dot{\rho}=k\qquad\qquad \dot{\varphi}=\Omega\qquad\qquad \rho\dot{\varphi} = k\Omega t$

lo que nos lleva a la respuesta D.

9.2 Pregunta 2

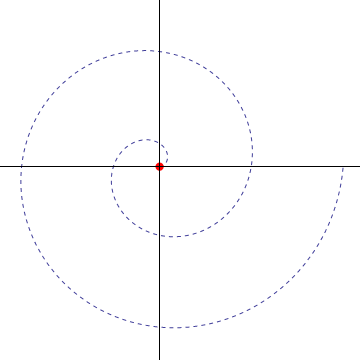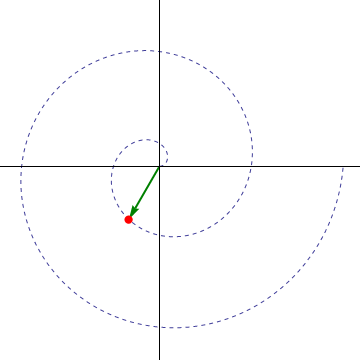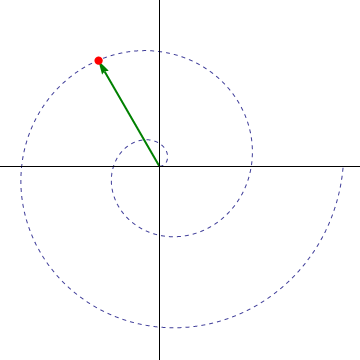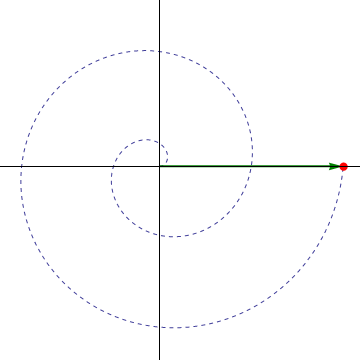
La trayectoria que describe la partícula es una…

A hélice.
B circunferencia.
C recta.
D espiral.

9.2.1 Solución

La respuesta correcta es la D.

Esta partícula se mueve de forma que va aumentando su distancia al origen (ρ va creciendo) al mismo tiempo que va girando en torno a él (φ va aumentando). Por tanto, la curva que describe es una espiral. Concretamente la llamada espiral de Arquímedes

10 Gráfica de un oscilador amortiguado

A un oscilador armónico con rozamiento viscoso sobreamortiguado, situado inicialmente en la posición de equilibrio se le comunica una cierta velocidad inicial. ¿Cuál de las cuatro figuras siguientes corresponde a su elongación como función del tiempo?

A	B


C	D

10.1 Solución

La respuesta correcta es la B.

Un oscilador sobreamortiguado se caracteriza por que no oscila, sino que decae exponencialmente hasta la posición de equilibrio. Esto nos deja con las respuestas B y D. Ahora bien, en este caso la partícula parte del origen con una cierta velocidad, es decir, está en x=0 en t=0. Por tanto la respuesta correcta es la B.

11 Victoria en una carrera

En una carrera de 400 m, los atletas deben dar una vuelta completa al estadio, coincidiendo la meta con la salida. En esta carrera el ganador es el que tenga la mayor…

A velocidad instantánea.
B rapidez (o celeridad) instantánea.
C velocidad media.
D rapidez (o celeridad) media.

11.1 Solución

La respuesta correcta es la D.

Gana la carrera el que menos tarde en recorrer la distancia dada, que es la misma para todos. Si la rapidez media es igual a

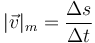
$|\vec{v}|_m = \frac{\Delta s}{\Delta t}$

se tiene que gana el que tenga mayor rapidez media.

No la velocidad media, ya que la velocidad se refiere al desplazamiento como vector, que es nulo en este caso para todos los corredores; ni tampoco los valores instantáneos, que nos informan de lo que hacen en un momento dado, pero no en el global de la carrera.

12 Colisión de un neutrón

Un neutrón de masa $m$ viaja con velocidad 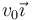$v_0\vec{\imath}$ e impacta frontalmente contra un núcleo de helio de masa $4 m$ que se encuentra en reposo. Tras la colisión, el neutrón se queda en reposo.

12.1 Pregunta 1

¿Cuál es la velocidad del centro de masas del sistema después de la colisión?

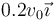
A $0.2v_0\vec{\imath}$
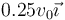
B $0.25v_0\vec{\imath}$
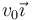
C $v_0\vec{\imath}$
D $0.5v_0\vec{\imath}$

12.1.1 Solución

La respuesta correcta es la A.

En una colisión, la velocidad del centro de masas es la misma antes y depués de ella, por la conservación de la cantidad de movimiento

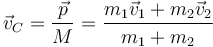
$\vec{v}_C=\frac{\vec{p}}{M}=\frac{m_1\vec{v}_1+m_2\vec{v}_2}{m_1+m_2}$

siendo su valor

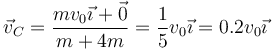
$\vec{v}_C=\frac{mv_0\vec{\imath}+\vec{0}}{m+4m}=\frac{1}{5}v_0\vec{\imath}=0.2v_0\vec{\imath}$

12.2 Pregunta 2

¿Es esta colisión elástica o inelástica?

A No hay información suficiente para saberlo.
B Elástica.
C Inelástica.
D Es imposible que el neutrón se quede parado tras la colisión.

12.2.1 Solución

La respuesta correcta es la C.

La energía cinética inicial es

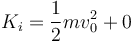
$K_i = \frac{1}{2}mv_0^2 + 0$

Para la final, calculamos la velocidad que adquiere el núcleo de helio. Por la conservación de la cantidad de movimiento

$mv_0\vec{\imath} + 4m\vec{0}= m\vec{0}+4m\vec{v}_{2f}\qquad\Rightarrow\qquad \vec{v}_{2f}=\frac{v_0}{4}\vec{\imath}$

y por tanto la energía cinética vale

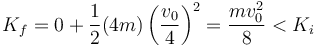
$K_f = 0+\frac{1}{2}(4m)\left(\frac{v_0}{4}\right)^2 = \frac{mv_0^2}{8} < K_i$

Se pierde energía cinética y por tanto la colisión es inelástica.

También puede verse a partir del coeficiente de restitución

$C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}}=-\frac{v_0/4-0}{0-v_0}=\frac{1}{4}$

o simplemente observando que si fuera una colisión elástica, la partícula más ligera rebotaría hacia atrás.

Test de la tercera convocatoria de Física I 2013-2014 (GIE)

De Laplace

Contenido

1 Movimiento de una L

1.1 Pregunta 1

1.1.1 Solución

1.2 Pregunta 2

1.2.1 Solución

2 Relación del ergio con el julio

2.1 Solución

3 Partícula sometida a dos fuerzas

3.1 Solución

4 Partícula sometida a un potencial

4.1 Pregunta 1

4.1.1 Solución

4.2 Pregunta 2

4.2.1 Solución

5 Propiedad de un m.a.s.

5.1 Solución

6 Ángulo entre velocidad y aceleración

6.1 Solución

7 Conservación en un sistema cerrado

7.1 Solución

8 Movimiento con potencia constante

8.1 Solución

9 Movimiento en polares

9.1 Pregunta 1

9.1.1 Solución

9.2 Pregunta 2

9.2.1 Solución

10 Gráfica de un oscilador amortiguado

10.1 Solución

11 Victoria en una carrera

11.1 Solución

12 Colisión de un neutrón

12.1 Pregunta 1

12.1.1 Solución

12.2 Pregunta 2

12.2.1 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES