Leyes de conservación en un sistema de partículas
De Laplace
Contenido |
1 Leyes de conservación
La utilidad de las definiciones del centro de masas y las propiedades colectivas de un sistema de partículas se pone de manifiesto cuando se estudia cómo varían en el tiempo y en qué casos son constantes de movimiento.
2 De la cantidad de movimiento
Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es

esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas

y la derivada de la cantidad de movimiento queda

Pero, de acuerdo con la tercera ley de Newton

y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil

siendo  la resultante de las fuerzas externas aplicadas, esto es
la resultante de las fuerzas externas aplicadas, esto es
- la derivada de la cantidad de movimiento es igual a la resultante de las fuerzas externas aplicadas sobre el sistema.
- En particular: En ausencia de fuerzas externas, la cantidad de movimiento de un sistema de partículas permanece constante.
En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe
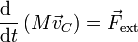
es decir:
- El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se encontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema.
- En particular, el centro de masas de un sistema de partículas sometidas exclusivamente a fuerzas internas permanece en reposo o en un estado de movimiento uniforme.
En un sistema cerrado, en el que la masa total permanece constante, la derivada de la masa es cero y obtenemos
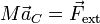
Como ejemplo tenemos el lanzamiento de un objeto. Aunque las distintas partes del objeto pueden seguir trayectorias complicadas, su CM se mueve como una partícula sometida exclusivamente a la acción del peso, es decir, describe una parábola
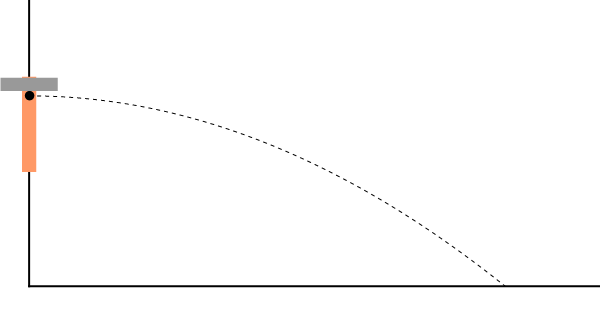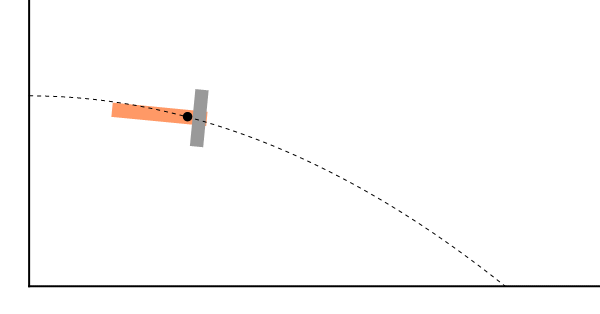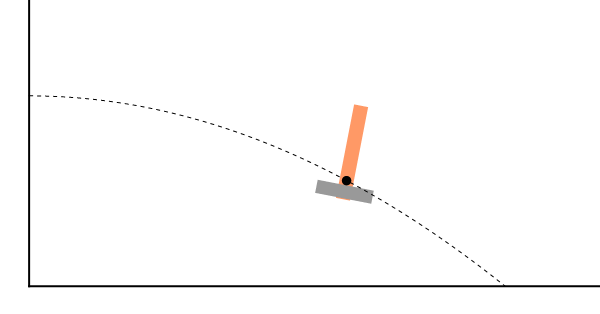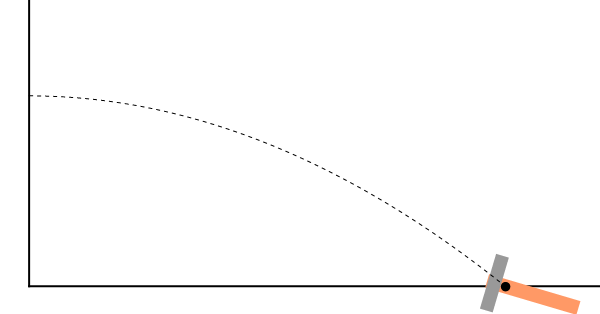
Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide.
3 Del momento cinético
Derivando igualmente en la expresión del momento cinético de un sistema de partículas obtenemos
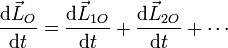
Para cada partícula la derivada del momento angular es el momento de las fuerzas aplicadas sobre ella:
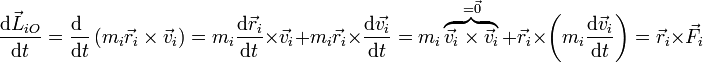
y, para el momento cinético total
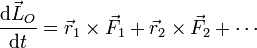
De nuevo, esta expresión requiere conocer las fuerzas internas del sistema, que son usualmente desconocidas. Por ello, descomponemos de nuevo en sumas de fuerzas externas e internas

Las fuerzas newtonianas, que verifican la tercera ley de Newton, no solo cumplen que son iguales y opuestas, sino que además van en la dirección de la recta que une las dos partículas

Combinando las dos ecuaciones queda
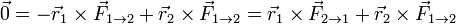
esto es, los momentos de las fuerzas internas se anulan mutuamente. Esta condición se cumple en la mayoría de los casos prácticos (fuerzas eléctricas o gravitatorias). En este caso, los momentos de las fuerzas internas se anulan dos a dos y queda
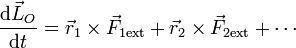
En palabras:
- La derivada del momento angular o cinético de un sistema de partículas es igual a la suma de los momentos de las fuerzas externas aplicadas sobre el sistema.
- En particular, en un sistema de partículas sometido exclusivamente a fuerzas internas, el momento angular permanece constante.
4 El caso de la energía cinética
Para la energía cinética no existe un teorema tan simple como para la cantidad de movimiento o el momento cinético. Operando del mismo modo que para estas dos cantidades, en sencillo probar que
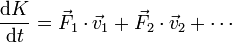
esto es, la derivada de la energía cinética es la potencia desarrollada por todas las fuerzas ejercidas en el sistema. Sin embargo, en este caso, no podemos eliminar las fuerzas internas de la ecuación. La razón es que las fuerzas internas sí pueden variar la energía cinética total.
Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total.





