Test de la 1ª convocatoria CMR 2017-2018

De Laplace

Contenido

1 Plato en rotación
- 1.1 Pregunta 1
- 1.2 Pregunta 2
2 Fuerza central
3 Sistema de tres fuerzas
4 Tensor de inercia
- 4.1 Pregunta 1
- 4.2 Pregunta 2
5 Vínculos entre dos masas
6 Masa en plano inclinado móvil
- 6.1 Pregunta 1
- 6.2 Pregunta 2

1 Plato en rotación

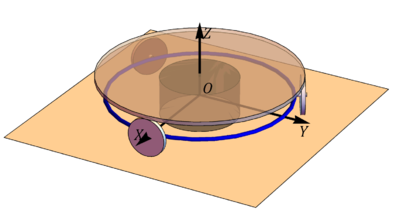
El plato de un microondas es un disco de radio $R$ ("sólido 2"), que gira con velocidad angular 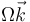$\Omega\vec{k}$ alrededor de su eje $O Z 1$ . Para que no roce con la caja, se apoya sobre tres ruedecillas de radio $r$ (siendo una de ellas el sólido “3”), montadas sobre un aro de plástico también de radio $R$ . El contacto del plato con las ruedecillas y de éstas con el suelo del horno es de rodadura sin deslizamiento. Se toma un sistema de ejes en el que el $O Z 0$ es el eje del plato y el $O X 0$ el horizontal que pasa por el centro de la ruedecilla “3”.

1.1 Pregunta 1

¿Cuál es la velocidad angular, respecto al suelo, del aro donde van montados las ruedecillas?

A $\vec{0}$ .
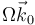B $\Omega\vec{k}_0$ .
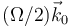C $(\Omega/2) \vec{k}_0$ .
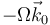D $-\Omega\vec{k}_0$ .

Solución

La respuesta correcta es la C.

Puesto que la ruedecilla rueda sin deslizar sobre el disco, la velocidad del punto B, de contacto con el disco, es la misma que la del disco en ese punto

La velocidad del punto A, de contacto con el suelo, es nula, por estar rodando también sin deslizar

El centro del disco C, situado en el punto medio entre A y B, posee una velocidad que es la media de estas dos. O dicho de otra manera, el punto superior de una rueda se mueve al doble de velocidad que el centro

Este punto también pertenece al sólido 0 y por tanto la velocidad angular del aro es la mitad que la del disco

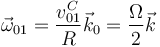
$\vec{\omega}_{01}=\frac{v^C_{01}}{R}\vec{k}_0=\frac{\Omega}{2}\vec{k}$

1.2 Pregunta 2

¿Cuánto vale la velocidad angular de la ruedecilla respecto a su eje, $O X 0$ ?

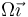A $\Omega\vec{\imath}$ .
B 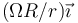$(\Omega R/r) \vec{\imath}$ .
C $-(\Omega R/2r) \vec{\imath}$ .
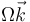D $\Omega\vec{k}$ .

Solución

La respuesta correcta es la C.

Respecto al sólido 1, el punto C avanza con velocidad

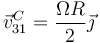
$\vec{v}^C_{31}=\frac{\Omega R}{2}\vec{\jmath}$

y el punto A está inmóvil

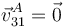
$\vec{v}^A_{31}=\vec{0}$

Respecto al sólido 0, el punto C estará inmóvil, mientras que A retrocede con velocidad

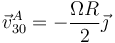
$\vec{v}^A_{30}=-\frac{\Omega R}{2}\vec{\jmath}$

y al estar C en el eje de rotación de este movimiento

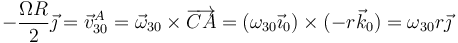
$-\frac{\Omega R}{2}\vec{\jmath}=\vec{v}^A_{30}=\vec{\omega}_{30}\times\overrightarrow{CA}=(\omega_{30}\vec{\imath}_0)\times(-r\vec{k}_0)=\omega_{30}r\vec{\jmath}$

por lo que

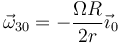
$\vec{\omega}_{30}=-\frac{\Omega R}{2r}\vec{\imath}_0$

2 Fuerza central

Una partícula se mueve sobre el espacio sometida exclusivamente a la acción de una fuerza central con centro O, 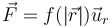$\vec{F}=f(|\vec{r}|)\vec{u}_r$ . ¿Cuál de las siguientes cantidades no es una constante de movimiento?

A La energía mecánica
B El momento cinético respecto a O, el origen de coordenadas.
C La cantidad de movimiento.
D La masa de la partícula.

Solución

La respuesta correcta es la C.

Por la segunda ley de Newton

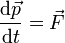
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\vec{F}$

Por tanto, si hay una fuerza actuando sobre la partícula, su cantidad de movimiento no es constante.

3 Sistema de tres fuerzas

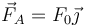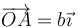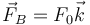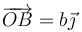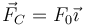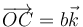Un sólido está sometido al sistema de tres fuerzas $\vec{F}_A=F_0 \vec{\jmath}$ aplicada en $\overrightarrow{OA}=b\vec{\imath}$ , $\vec{F}_B=F_0 \vec{k}$ aplicada en $\overrightarrow{OB}=b\vec{\jmath}$ y $\vec{F}_C=F_0 \vec{\imath}$ aplicada en $\overrightarrow{OC}=b\vec{k}$ . Este sistema de fuerzas es equivalente a…

A un sistema nulo.
B un par de fuerzas.
C una fuerza única.
D un tornillo.

Solución

La respuesta correcta es la D.

Aplicamos el esquema

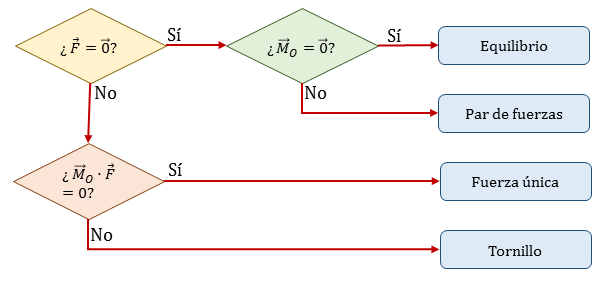
La resultante del sistema no es nula:

$\vec{F}=\vec{F}_A+\vec{F}_B+\vec{F}_C=F_0(\vec{\imath}+\vec{\jmath}+\vec{k})$

Por tanto, no puede ser ni un sistema nulo ni un par de fuerzas.

Hallamos el momento respecto a O

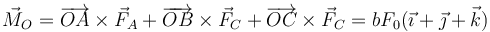
$\vec{M}_O=\overrightarrow{OA}\times\vec{F}_A+\overrightarrow{OB}\times\vec{F}_C+\overrightarrow{OC}\times\vec{F}_C=bF_0(\vec{\imath}+\vec{\jmath}+\vec{k})$

Este momento no es perpendicular a $\vec{F}$ (de hecho, es paralelo a la resultante). Por tanto, el sistema equivale a un tornillo.

4 Tensor de inercia

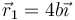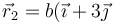Un sólido está formado por dos masas iguales, $m 1 = m 2 = m$ , unidas por una varilla sin masa. las dos partículas se hallan en $\vec{r}_1=4b\vec{\imath}$ y $\vec{r}_2=b(\vec{\imath}+3\vec{\jmath}$ ), respectivamente.

4.1 Pregunta 1

¿Cuánto vale su tensor de inercia respecto al triedro OXYZ?

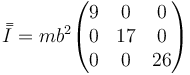
A $\bar{\bar{I}}=mb^2\begin{pmatrix}9 & 0 & 0\\0 & 17 & 0 \\ 0 & 0 & 26\end{pmatrix}$
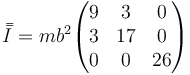
B $\bar{\bar{I}}=mb^2\begin{pmatrix}9 & 3 & 0\\3 & 17 & 0 \\ 0 & 0 & 26\end{pmatrix}$
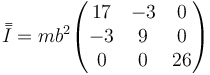
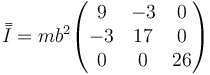
C $\bar{\bar{I}}=mb^2\begin{pmatrix}17 & -3 & 0\\-3 & 9 & 0 \\ 0 & 0 & 26\end{pmatrix}$
D $\bar{\bar{I}}=mb^2\begin{pmatrix}9 & -3 & 0\\-3 & 17 & 0 \\ 0 & 0 & 26\end{pmatrix}$

Solución

La respuesta correcta es la D.

Los elementos diagonales del tensor de inercia son los momentos de inercia

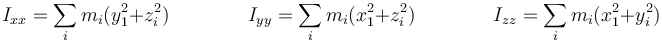
$I_{xx}=\sum_i m_i(y_1^2+z_i^2)\qquad\qquad I_{yy}=\sum_i m_i(x_1^2+z_i^2)\qquad\qquad I_{zz}=\sum_i m_i(x_1^2+y_i^2)$

y los no diagonales son los productos de inercia cambiados de signo

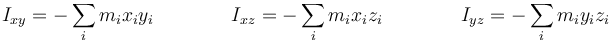
$I_{xy}=-\sum_i m_i x_iy_i\qquad\qquad I_{xz}=-\sum_i m_i x_iz_i\qquad\qquad I_{yz}=-\sum_i m_i y_iz_i$

Como solo tenemos dos masas, no hay problema en hallar cada elemento, pero comparando los resultados propuesto basta con hallar $I x x$ e $I x y$

$I_{xx} = m(0+0)+m(3b)^2 = 9mb^2\qquad\qquad I_{xy}=-m(4b)0-mb(3b)=-3mb^2$

y vemos que la correcta es la D.

4.2 Pregunta 2

¿Cuál de los siguientes es un eje principal de inercia de este sólido respecto al punto O?

A OX
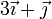
B La recta que pasa por O y lleva la dirección de $3\vec{\imath}+\vec{\jmath}$
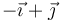
C La recta que pasa por O y lleva la dirección de $-\vec{\imath}+\vec{\jmath}$
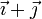
D La recta que pasa por O y lleva la dirección de $\vec{\imath}+\vec{\jmath}$

Solución

La respuesta correcta es la B.

Si $\vec{u}$ va en la dirección d eun vector principal se cumple que

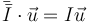
$\bar{\bar{I}}\cdot\vec{u}=I\vec{u}$

es decir el producto por el tensor de inercia produce un vector paralelo al original.

Aplicando esto a los diferentes vectores de las opciones resulta para la opción B

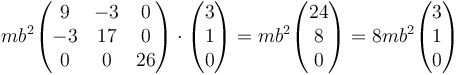
$mb^2\begin{pmatrix}9 & -3 & 0\\-3 & 17 & 0 \\ 0 & 0 & 26\end{pmatrix} \cdot \begin{pmatrix} 3 \\ 1 \\ 0\end{pmatrix} = mb^2 \begin{pmatrix} 24 \\ 8 \\ 0\end{pmatrix}= 8mb^2\begin{pmatrix} 3 \\ 1 \\ 0\end{pmatrix}$

por lo que ésta es una dirección principal, siendo el momento principal de inercia $8 m b 2$ .

5 Vínculos entre dos masas

Un sistema está formado por dos masas iguales situadas sobre una superficie horizontal unidas por una varilla rígida de longitud $b$ . La masa 2 puede deslizar sin rozamiento sobre la superficie mientras que la masa 1 está montada sobre una cuchilla ortogonal a la varilla. La cuchilla impide el movimiento perpendicular a su orientación.

¿Cuál de los siguientes no es un vínculo sobre el sistema?

A $(x 2 - x 1) 2 + (y 2 - y 1) 2 = b 2$
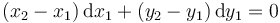
B $(x_2-x_1 )\,\mathrm{d}x_1+(y_2-y_1 )\,\mathrm{d}y_1=0$
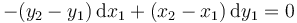
C $-(y_2-y_1 )\,\mathrm{d}x_1+(x_2-x_1 )\,\mathrm{d}y_1=0$
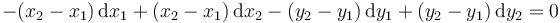
D $-(x_2-x_1 )\,\mathrm{d}x_1+(x_2-x_1 )\,\mathrm{d}x_2-(y_2-y_1 )\,\mathrm{d}y_1+(y_2-y_1 )\,\mathrm{d}y_2=0$

Solución

La respuesta correcta es la C.

Las dos masas están a una cierta distancia fijada, por lo que cumple el vínculo A

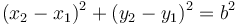
$(x_2-x_1 )^2+(y_2-y_1 )^2=b^2\,$

Si hallamos la forma pfaffiana de este vínculo obtenemos la opción D

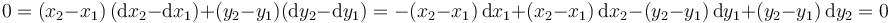
$0=(x_2-x_1 )\,(\mathrm{d}x_2-\mathrm{d}x_1)+(y_2-y_1 )(\mathrm{d}y_2-\mathrm{d}y_1)=-(x_2-x_1 )\,\mathrm{d}x_1+(x_2-x_1 )\,\mathrm{d}x_2-(y_2-y_1 )\,\mathrm{d}y_1+(y_2-y_1 )\,\mathrm{d}y_2=0$

Por otro lado, el desplazamiento de la masa 1 debe ser perpendicular a la varilla

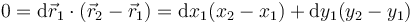
$0=\mathrm{d}\vec{r}_1\cdot(\vec{r}_2-\vec{r}_1)=\mathrm{d}x_1(x_2-x_1)+\mathrm{d}y_1(y_2-y_1)$

que es la opción B.

6 Masa en plano inclinado móvil

Se tiene un sistema plano formado por un bloque triangular de masa $m 1$ , altura h e inclinación β sobre el cual se encuentra una masa m_2. Esta masa puede deslizar sin rozamiento sobre el bloque. Éste, a su vez, puede deslizar sin rozamiento sobre una superficie horizontal. Sea s la distancia de $m 2$ al vértice superior del bloque y sea x la distancia horizontal del bloque a un punto fijo. Abreviamos C=cos⁡(β), S=sen⁡(β)

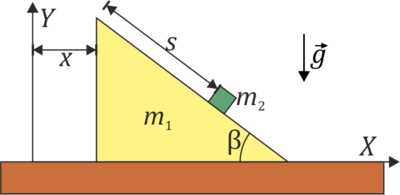
6.1 Pregunta 1

La lagrangiana de este sistema es, teniendo en cuenta que siempre se puede sumar una constante,…

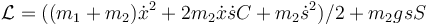
A $\mathcal{L}=((m_1+m_2 )\dot{x}^2+2m_2\dot{x}\dot{s}C+m_2 \dot{s}^2 )/2+m_2 gsS$
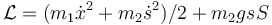
B $\mathcal{L}=(m_1 \dot{x}^2+m_2 \dot{s}^2 )/2+m_2 gsS$
C $\mathcal{L}=((m_1+m_2 ) \dot{x}^2+m_2 \dot{s}^2 )/2-m_2 gsS$
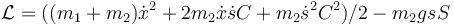
D $\mathcal{L}=((m_1+m_2 ) \dot{x}^2+2m_2 \dot{x}\dot{s}C+m_2 \dot{s}^2 C^2 )/2-m_2 gsS$

Solución

La respuesta correcta es la A.

La energía cinética del bloque es simplemente

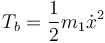
$T_b=\frac{1}{2}m_1\dot{x}^2$

La de la partícula es

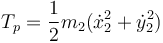
$T_p=\frac{1}{2}m_2(\dot{x}_2^2+\dot{y}_2^2)$

siendo

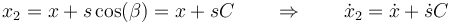
$x_2=x+s\cos(\beta)=x+sC\qquad\Rightarrow\qquad \dot{x}_2=\dot{x}+\dot{s}C$

y

$y_2=h-s\,\mathrm{sen}(\beta)=h-sS\qquad\Rightarrow\qquad \dot{y}_2=-\dot{s}S$

Sustituyendo nos queda la energía cinética total

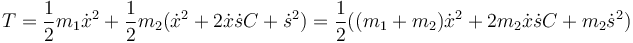
$T=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2(\dot{x}^2+2\dot{x}\dot{s}C+\dot{s}^2)=\frac{1}{2}((m_1+m_2)\dot{x}^2+2m_2\dot{x}\dot{s}C+m_2\dot{s}^2)$

Esto ya nos permite identificar la respuesta correcta. El último término corresponde a la energía potencial

$U=m_2gy_2=m_2gh-m_2gsS = U_0-m_2gsS\,$

La constante se puede omitir, ya que desaparece al derivar para hallar las ecuaciones de Lagrange.

6.2 Pregunta 2

¿Cuánto valen las aceleraciones de las coordenadas x y s?

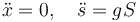
A $\ddot{x}=0,\quad \ddot{s}=gS$
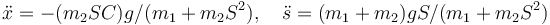
B $\ddot{x}=-(m_2 SC)g/(m_1+m_2 S^2 ),\quad\ddot{s}=(m_1+m_2 )gS/(m_1+m_2 S^2 )$
C $\ddot{x}=-m_2g/(m_1+m_2 ), \quad \ddot{s}=(m_1 Sg/(m_1+m_2 )$
D $\ddot{x}=0, \quad \ddot{s}=m_1 Sg/(m_1+m_2 )$

Solución

La respuesta correcta es la C.

Hallamos las ecuaciones de movimiento a partir de las ecuaciones de Lagrange. Para x tenemos

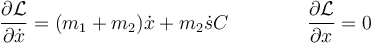
$\frac{\partial\mathcal{L}}{\partial \dot{x}}=(m_1+m_2)\dot{x}+m_2 \dot{s}C\qquad\qquad \frac{\partial\mathcal{L}}{\partial x}=0$

lo que da

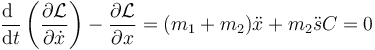
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial \dot{x}}\right)-\frac{\partial\mathcal{L}}{\partial x}=(m_1+m_2)\ddot{x}+m_2 \ddot{s}C=0$

Para s tenemos

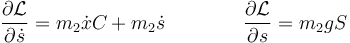
$\frac{\partial\mathcal{L}}{\partial \dot{s}}=m_2 \dot{x}C+m_2\dot{s}\qquad\qquad \frac{\partial\mathcal{L}}{\partial s}=m_2gS$

lo que da

$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial \dot{s}}\right)-\frac{\partial\mathcal{L}}{\partial s}=m_2 \ddot{x}C+m_2\ddot{s}-m_2gS=0$

De la primera despejamos 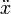$\ddot{x}$

$\ddot{x}=-\frac{m_2C}{m_1+m_2}\ddot{s}$

y sustituimos en la segunda

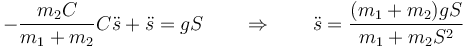
$-\frac{m_2C}{m_1+m_2}C\ddot{s}+\ddot{s}=gS\qquad\Rightarrow\qquad \ddot{s}=\frac{(m_1+m_2)gS}{m_1+m_2S^2}$

Para x queda la aceleración

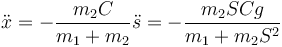
$\ddot{x}=-\frac{m_2C}{m_1+m_2}\ddot{s}=-\frac{m_2SCg}{m_1+m_2S^2}$

Cuando la masa desciende se conserva la cantidad de movimiento horizontal, por lo que si la masa va hacia la derecha, el bloque debe acelerarse hacia la izquierda.

Test de la 1ª convocatoria CMR 2017-2018

De Laplace

Contenido

1 Plato en rotación

1.1 Pregunta 1

1.2 Pregunta 2

2 Fuerza central

3 Sistema de tres fuerzas

4 Tensor de inercia

4.1 Pregunta 1

4.2 Pregunta 2

5 Vínculos entre dos masas

6 Masa en plano inclinado móvil

6.1 Pregunta 1

6.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES