Sistema de dos partículas
De Laplace
Contenido |
1 Sistema de dos partículas
2 Explosión de un proyectil
Supongamos un proyectil de masa M que es disparado con un mortero desde el suelo. Cuando el proyectil lleva recorrida horizontalmente una distancia a y se encuentra en el punto más alto de la parábola, se parte en dos pedazos desiguales. Uno de ellos, de masa M / 3 cae justo en la vertical del punto de explosión. El segundo fragmento impacta en el suelo al mismo tiempo que el primero. ¿A qué distancia del primero?
Una forma de resolver esto sería determinar la velocidad del segundo fragmento inmediatamente tras la explosión y estudiar su movimiento parabólíco siguiente, para hallar su alcance, pero no se nos dice ni la velocidad inicial, ni el ángulo con que fue disparado el proyectil.
Lo más sencillo es utilizar que el centro de masas se mueve como una partícula sometida a la resultante de las fuerzas externas, en este caso, el peso total. Por tanto, describe el arco de parábola completo, hasta impactar en el suelo, a una distancia 2a del punto del disparo.
Si el fragmento de masa M / 3 se encuentra en x1 = a y el centro de masas en xC = 2a, ambos a la altura y = 0, la posición del segundo fragmento la obtenemos de
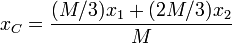
 3xC = x1 + 2x2
3xC = x1 + 2x2  6a = a + 2x2
6a = a + 2x2 
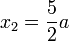
3 Dos partículas unidas por un oscilador armónico
Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad v0 alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?
4 Dos partículas unidas por una barra
Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que puden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v0 perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?





