Primera convocatoria 2014/15 (F2GIA)

De Laplace

1 Esfera con huecos cargados y condensador

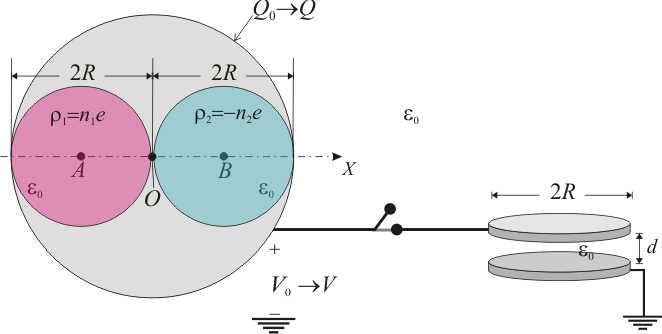
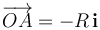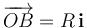Una esfera conductora de radio $2 R$ y centro $O$ tiene practicados en su interior dos huecos esféricos tangentes pero no conectados, ambos de radio $R$ , de centros $A$ y $B$ , de manera que $\overrightarrow{OA}=-R\!\ \mathbf{i}$ , y $\overrightarrow{OB}=R\!\ \mathbf{i}$ . Inicialmente, los huecos están vacíos y la esfera descargada.

Se procede a introducir en los huecos sendos gases ionizados, con iones de distinto signo y en concentraciones $n 1$ y $n 2$ lo suficientemente bajas como para poder considerar que las correspondientes cargas eléctricas se distribuyen uniformemente en cada uno de los volúmenes; así en el hueco de centro $A$ hay una densidad volumétrica de carga constante 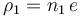$\rho_1=n_1\!\ e$ , y en la de centro $B$ , es $\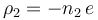rho_2=-n_2\!\ e$ .

Obtenga las expresiones de las magnitudes que se indican a continuación, en función de los parámetros descritos, una vez que el sistema recupera el equilibrio electrostático

a) Carga eléctrica libre,

Q 0

, en la superficie exterior de la esfera conductora, y densidad superficial que describe su distribución.

b) Campo eléctrico dentro de cada uno de los huecos con gas ionizado.

c) Valor

V 0

del potencial electrostático a que se encuentra la esfera conductora. Diferencia de potencial entre los centros

A

y

B

de los huecos.

A continuación, la esfera se conecta mediante un cable conductor muy largo a un disco conductor de radio $R$ , que se encuentra separado una distancia $d$ de otro disco idéntico conectado a tierra, formando ambos un condensador plano paralelo. El espacio entre los discos está relleno de aire.

En este nuevo sistema...

d) ¿Qué relación deben verificar

R

y

d

para que la carga

Q 0

de la superficie conductora se reparta a partes iguales entre ésta y el disco del condensador al cuál está conectada?

e) Determine la expresión del potencial electrostático

V

en la esfera conductora y el disco, en función de los parámetros

R

y

d

.

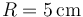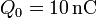f) Considérese el caso $R=5\,\mathrm{cm}$ y $Q_0=10\,\mathrm{nC}$ . Determine el valor mínimo posible para la distancia

d

de separación entre discos.

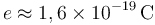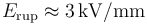Datos: carga elemental: $\;\displaystyle e\approx 1,6\times 10^{-19}\,\mathrm{C}$ ; campo de ruptura dieléctrica del aire, $E_\mathrm{rup}\approx 3\,\mathrm{kV/mm}$ .

2 Circuito eléctrico con bombilla móvil

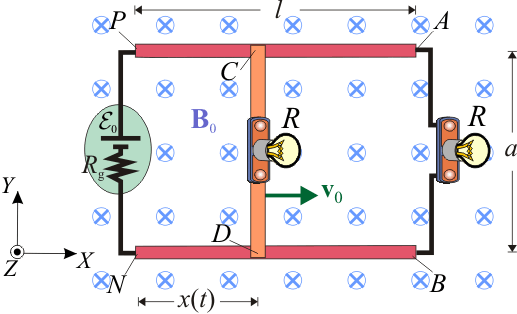
El circuito eléctrico de la figura está formado por dos regletas conductoras, ambas de longitud $l$ , dispuestas en paralelo y separadas por una distancia fija $a$ . Sendos extremos de dichas regletas están conectados a los electrodos $P$ y $N$ de un generador d.c. (batería), cuya f.e.m. tiene un valor constante 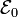$\mathcal{E}_0$ y una resistencia interna $R g$ . Los otros extremos de las dos regletas, $A$ y $B$ , se conectan a través de una bombilla incandescente de resistencia $R$ . Además, se tienen otros dos segmentos conductores, alineados y conectados por otra bombilla idéntica a la anterior, y con los extremos libres, $C$ y $D$ , siempre en contacto con las regletas. El resto de resistencias eléctricas del sistema son despreciables frente al valor $R$ de las bombillas, excepto la resistencia interna del generador, que vale $R g = R / 2$ . Todo el sistema está sometido a un campo magnético uniforme 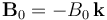$\mathbf{B}_0=-B_0\!\ \mathbf{k}$ perpendicular al plano $O X Y$ que contiene al circuito, y de sentido opuesto al eje $O Z$ , tal como se indica en la figura.

Inicialmente, la rama conductora $C D$ está en reposo, en contacto con los extremos de las regletas que se hallan conectados a la batería ( $P$ y $N$ ). En esta situación, obtenga las expresiones de las siguientes magnitudes en función de los parámetros indicados en el enunciado:

: a) Intensidad de corriente total suministrada por el generador, e intensidades en cada una de las ramas.; b) Expresión de la energía que por unidad de tiempo se disipa en cada resistencia. ¿Cómo serán, comparativamente, las intensidades luminosas de las bombillas?

A partir de un cierto instante, la rama

C D

con bombilla incluida, se desplaza hacia la bombilla fija que cierra el circuito entre

A

y

B

, manteniéndose perpendicular a las regletas conductoras y alcanzando una velocidad constante de valor

v 0

. En esta nueva situación, obtenga las expresiones de:

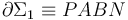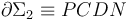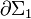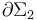: c) Flujos magnéticos a través de las espiras $\partial \Sigma_1\equiv PABN$ y $\partial \Sigma_2\equiv PCDN$ , y fuerzas electromotrices inducidas en cada una de ellas.; d) Ecuaciones del circuito en las espiras $\partial \Sigma_1$ y $\partial \Sigma_2$ .; e) Intensidades de las corrientes eléctricas que recorren el generador y cada una de las dos bombillas. ¿Qué puede decir acerca de las intensidades luminosas de las bombillas en relación con las iniciales? ¿Podría llegar a apagarse alguna de ellas?