Primera Convocatoria Ordinaria 2020/21 (G.I.E.R.M.)

De Laplace

Contenido

1 Barra con extremo en un arco de circunferencia
2 Partícula colgando de una cuerda con longitud variable
3 Disco con muelle enganchado en su centro
4 Partícula moviéndose en una elipse sometida a una fuerza central

1 Barra con extremo en un arco de circunferencia

El extremo $A$ de la barra de la figura (sólido "2") desliza sobre el eje fijo $O X 1$ . El otro extremo $B$ se mueve a lo largo de un arco de circunferencia de radio $R = 10 b$ (sólido "1"). La velocidad respecto al eje $O X 1$ del extremo $A$ de la barra es constante y de módulo $v 0$ . En el instante indicado en la figura el ángulo $β$ verifica

$\mathrm{sen}\,\beta = 4/5, \qquad \cos\beta = 3/5.$

Escribe la expresión del vector 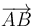$\overrightarrow{AB}$ en la base del sólido "1".
Encuentra gráficamente y analíticamente la posición del C.I.R. del movimiento {21} (puedes hacer la determinación gráfica en el propio dibujo)
Encuentra la reducción cinemática del movimiento {21} en el punto $A$ .

2 Partícula colgando de una cuerda con longitud variable

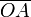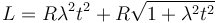El punto $A$ recorre la línea de puntos con rapidez constante $v 0 = λ R$ , siendo $λ$ una constante. La masa $m$ cuelga de una cuerda que desliza sobre el punto $A$ . La longitud total de la cuerda (es decir, la suma de las longitudes $\overline{OA}$ y $\overline{AB}$ ) varía en el tiempo según la ley $L = R\lambda^2 t^2 + R\sqrt{1+\lambda^2t^2}$ . Esto puede realizarse con un pequeño motor que desenrolle la cuerda en $O$ . En el instante inicial el punto $A$ se encontraba sobre el eje $Y$ . Durante todo el movimiento el trozo de cuerda entre $A$ y $B$ se mantiene vertical.

Escribe el vector 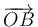$\overrightarrow{OB}$ . ¿Que tipo de curva describe la masa?
Calcula la velocidad y aceleración de la masa en todo instante de tiempo.
Calcula fuerza que la cuerda ejerce sobre la masa y la potencia que le transmite.

3 Disco con muelle enganchado en su centro

Un disco de masa $m$ y radio $R$ rueda sin deslizar sobre una superficie horizontal rugosa. El centro del disco está conectado al punto $A$ con un muelle de constante elástica $k = m g / R$ y longitud natural nula. Además, actúa sobre el disco un par de fuerzas 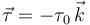$\vec{\tau}=-\tau_0\,\vec{k}$ , con $τ 0 > 0$ . En el instante inicial el disco estaba en reposo y su centro se encontraba sobre el eje $Y$ .

Dibuja el diagrama de cuerpo libre del disco.
Calcula la aceleración del centro del disco.
Si $τ 0 = m g R$ , ¿para que valor de $x$ el disco empieza a deslizar?

4 Partícula moviéndose en una elipse sometida a una fuerza central

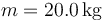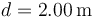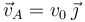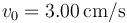Una partícula de masa $m=20.0\,\mathrm{kg}$ recorre una trayectoria elíptica en el plano $X Y$ . La ecuación de la elipse es $(x / 2 d) 2 + (y / d) 2 = 1$ , con $d=2.00\,\mathrm{m}$ . En el instante inicial la partícula se encontraba en el punto $A$ con velocidad $\vec{v}_A=v_0\,\vec{\jmath}$ , siendo $v_0=3.00\,\mathrm{cm/s}$ . Durante su movimiento la partícula se encuentra sometida a una fuerza dirigida siempre hacia el origen $O$ .