Preguntas de test del Primer Principio de la Termodinámica (GIE)
De Laplace
1 Calor en el calentamiento de un gas
Si un gas ideal se calienta a presión constante, ¿cómo se relacionan el calor que entra y la variación de la energía interna?
- A Qin > ΔU
- B Qin < ΔU
- C Qin = ΔU
- D Puede darse cualquiera de las tres situaciones anteriores.
- Solución
La respuesta correcta es la A.
En cualquier proceso de un gas ideal

mientras que si es a presión constante
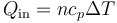
De acuerdo con la ley de Mayer para un gas ideal
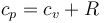
y por tanto

Otra forma de verlo es considerar que en un calentamiento a presión constante el gas se expande, por la ley de Charles, y por tanto realiza un trabajo sobre el entorno. Por la primera ley de la termodinámica

2 Energía y trabajo en el calentamiento de un gas
En una expansión cuasiestática de un gas ideal a presión constante, ¿cuánto vale el incremento de la energía interna del gas y el trabajo realizado sobre él?
- A
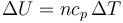 ;
; 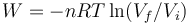 .
.
- B
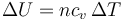 ;
; 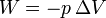 .
.
- C
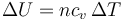 ;
; 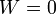 .
.
- D
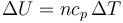 ;
; 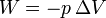 .
.
- A
- Solución
La respuesta correcta es la B.
La variación de la energía interna es independiente del proceso
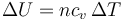
mientras que el trabajo realizado sobre el gas es
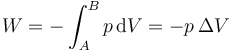
3 Mezcla de aguas
En un recipiente con paredes diatermas se mezclan 1000 cm³ de agua a 60 °C con 3000 cm³ de agua a 20 °C, que también es la temperatura exterior. ¿Cuál es la temperatura final del agua en el equilibrio?
- A 40°C
- B 30°C
- C 80°C
- D 20°C.
- Solución
La respuesta correcta es la D.
Si el sistema tiene paredes diatermas no está aislado térmicamente del exterior. Por tanto, su temperatura final será la del ambiente, que es 20 °C.
4 Trabajo en la fusión del hielo
Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0°C, al cual se le cede lentamente calor a una presión de 101.3 kPa hasta que convierte por completo en agua (densidad de masa 1000 kg/m³). ¿Qué trabajo se realiza sobre el sistema?
- A −9.15 J.
- B Ninguno.
- C +9.15 J.
- D −9.15 kJ.
- Solución
La respuesta correcta es la C.
De entrada puede parecer extraño que haya un trabajo en este proceso pues parece que al derretirse el hielo por calentamiento, nadie está haciendo fuerza sobre él, ni se está moviendo.
Pero no es así. Desde el mismo momento en que cambia el volumen, habiendo una presión externa, se está realizando trabajo. ¿Quién lo hace? El aire que rodea el hielo. Esa atmósfera de presión ejerce una fuerza sobre el hielo y lo comprime al pasar a la forma de agua. Si no estuviera el aire exterior, las moléculas de agua se desperdigarían y no formarían agua líquida.
El trabajo realizado a presión externa constante vale

Los volúmenes inicial y final los obtenemos de que conocemos la masa y la densidad. Para el hielo
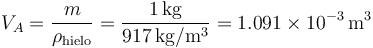
y para el agua
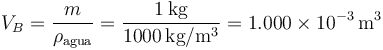
de forma que la variación del volumen es

Al fundirse el hielo, el volumen ocupado se reduce casi en un 10%.
El trabajo realizado vale
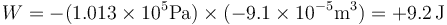
El trabajo es positivo ya que el aire exterior comprime al sistema.
5 Agua necesaria para fundir hielo
¿Cuanta agua a 20°C es aproximadamente necesaria para fundir por completo 100 g de hielo a 0°C?
- A 4.0 kg
- B 8.0 kg
- C 400 g
- D 80 kg
- Solución
La respuesta correcta es la C.
Para fundir el máximo de hielo posible debemos extraer el calor del agua, anfriándola hasta que esté en equilibrio con el hielo fundido (agua a 0°C). Entonces, usando lel SI
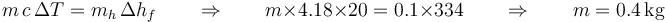
Este es un ejemplo en el que es algo más sencillo el usar unidades distintas del SI. Si se usan calorías en vez de julios, tenemos que

de donde

6 Comparación de tres procesos
Para los procesos cuasiestáticos de la figura, correspondientes a un gas ideal…

6.1 Pregunta 1
¿En cuál es mayor la variación de la energía interna?
- A En el proceso 3.
- B En el proceso 1.
- C Tiene el mismo valor en los tres procesos.
- D En el proceso 2.
- Solución
La respuesta correcta es la C.
La energía interna es una función de estado. Por tanto, su variación en un proceso depende solo de su valor en el estado final y el inicial. Puesto que estos son coincidentes para los tres procesos de la figura, la variación de energía interna es la misma en los tres casos.
6.2 Pregunta 2
¿En cuál es mayor el calor absorbido por el gas?
- A En el proceso 2.
- B En el proceso 1.
- C Tiene el mismo valor en los tres procesos.
- D En el proceso 3.
- Solución
La respuesta correcta es la B.
De acuerdo con el primer principio de la termodinámica
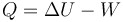
Puesto que la variación de la energía interna es la misma para los tres procesos y que el trabajo es positivo en los tres casos (se trata de compresiones), el calor mayor se obtendrá donde menor sea el trabajo. El trabajo es menor donde el área bajo la curva sea la más pequeña, lo cual ocurre en el proceso 1.
7 Expansión con aumento de presión
Se tiene una cantidad fija de un gas ideal diatómico situada a una presión p0, volumen V0 y temperatura T0. Experimenta un proceso tal que la presión final es 2p0 y el volumen 2V0.
7.1 Pregunta 1
El incremento de la energía interna en este proceso vale…
- A 0
- B (15 / 2)p0V0
- C − (15 / 2)p0V0
- D (5 / 2)p0V0
- Solución
La respuesta correcta es la B.
La variación de la energía interna depende solo de la variación en la temperatura
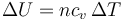
En el caso de un gas ideal diatómico cv = (5 / 2)R, por lo que
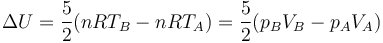
Sustituyendo los datos

7.2 Pregunta 2
Supongamos que el proceso anterior ocurre de manera cuasiestática según la ley
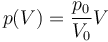
¿Cuánto trabajo se realiza sobre el gas en esta expansión cuasiestática?
- A + (3 / 2)p0V0
- B + (5 / 2)p0V0
- C − (3 / 2)p0V0
- D 0
- Solución
La respuesta correcta es la C.
En un proceso cuasiestático el trabajo se puede calcular mediante la integral
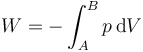
Sustituyendo la relación entre p y V
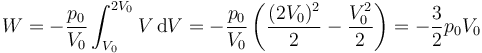
El trabajo es negativo pues se trata de una expansión en la que el gas hace trabajo sobre el ambiente.
7.3 Pregunta 3
¿Cuánto calor entra en el gas en la expansión cuasiestática?
- A − 9p0V0
- B 9p0V0
- C 0
- D Depende de si el recipiente es adiabático o no.
- Solución
La respuesta correcta es la B.
De acuerdo con el primer principio de la termodinámica
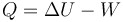
que en este caso nos da
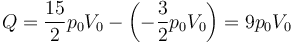
8 Equivalencia de una BTU
Una British Thermal Unit (BTU) es la energía necesaria para elevar la temperatura de 1 libra de agua (1 lb = 0.454 kg) de 39°F a 40°F (siendo 1.8°F = 1°C). Si el calor específico del agua es igual a 4.186 kJ/(kg·°C), ¿a qué equivale 1 BTU en el SI?
- A 3.420 kJ
- B 5.123 kJ
- C 1.055 kJ
- D 16.59 kJ
- Solución
La respuesta correcta es la C.
El calor necesario para elevar la temperatura de una cierta cantidad de agua es

siendo en este caso
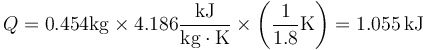
En primera aproximación, una BTU viene a ser lo mismo que un kilojulio.
9 Trabajo en un ciclo
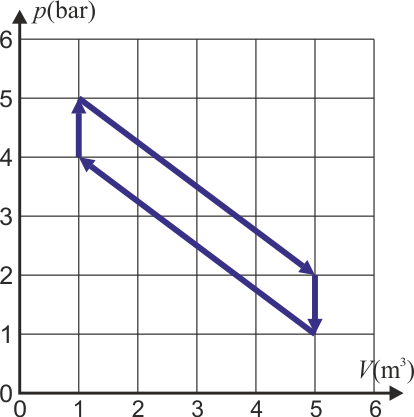
¿Qué trabajo neto realiza sobre el ambiente en un ciclo una máquina que realiza el siguiente ciclo termodinámico?
- A +400 kJ
- B −500 kJ
- C −400 kJ
- D +500 kJ
- Solución
La respuesta correcta es la A.
En un ciclo termodinámico, el trabajo realizado por el ambiente sobre la máquina es igual al área de la superficie encerrada, con signo positivo si se recorre en sentido antihorario (funciona como una estufa, absorbiendo trabajo y cediendo calor) y negativo si se recorre en sentido horario (funciona como un motor, absorbiendo calor y cediendo trabajo). Si lo que buscamos es el trabajo de la máquina sobre el ambiente, Wout se cambia el signo.
En este caso la figura es un paralelogramo, cuya área se calcula como base por altura, o bien se halla directamente con ayuda de la cuadrícula. La base (distancia en horizontal entre los lados verticales es
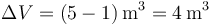
y la altura es la longitud de un tramo vertical
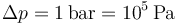
lo que da el trabajo
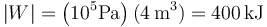
Este ciclo se recorre en sentido horario, por lo que se trata de un motor. El trabajo que realiza la máquina sobre el ambiente es positivo.
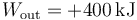
10 Tubo con dos cámaras
Un tubo de sección S está dividido en dos cámaras de longitud L. Las paredes son adiabáticas y la pared central es inamovible y está forrada de aislante térmico. Inicialmente, en la cámara de la izquierda (1) hay aire a temperatura T1 = T0 y presión p0 y en la de la derecha (2) aire a T2 = 3T0 y la misma presión. Se retira el aislante del tabique central (sin eliminar el tabique).

10.1 Pregunta 1
¿Cuál es la relación entre las masas de aire en las dos cámaras?
- A m2 = 3m1
- B m1 = m2
- C m1 = 9m2
- D m1 = 3m2
- Solución
La respuesta correcta es la D.
Para los dos cámaras se cumple la ley de los gases ideales
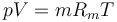
siendo en este caso iguales en las dos cámaras la constante de los gases (aire en ambas cámaras), la presión a la que se encuentran y el volumen que ocupan. Por tanto, se cumple
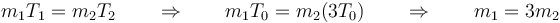
10.2 Pregunta 2
¿Qué ecuación, de las siguientes, permite calcular la temperatura de equilibrio final? (los subíndices se refieren a cada una de las dos cámaras).
- A ΔS1 + ΔS2 = 0
- B W2out = W1in
- C p1f = p2f, T1f = T2f.
- D ΔU1 + ΔU2 = 0
- Solución
La solución correcta es la D.
Una vez que se retira el aislante, pasa calor de la cámara más caliente a la más fría. Puesto que el volumen no cambia, esto implica un cambio en las presiones respectivas, por lo que se rompe el equilibrio mecánico. En el estado de equilibrio térmico final las presiones no son iguales y no se puede usar la opción C.
El proceso será en general irreversible, por lo que tampoco se puede aplicar que no hay variación de entropía (A).
Puesto que no hay cambio en el volumen de cada cámara no se realiza ningún trabajo, lo cual descarta la opción B (que es trivialmente cierta, 0 = 0, pero no es útil).
Queda la opción D. Puesto que el sistema completo está aislado térmicamente, no se intercambia calor con el exterior. Puesto que es rígido, tampoco hay trabajo. Por tanto, se conserva la energía interna. Lo que aumente la de uno de las cámaras será igual a lo que disminuya la de la otra.
10.3 Pregunta 3
¿Cuál es dicha temperatura final de las cámaras?
- A Tf = 4T0
- B Tf = 2T0
- C Tf = T0
- D Tf = 3T0 / 2
- Solución
La respuesta correcta es la D.
Aplicando la ecuación del apartado anterior

lo que da
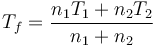
puesto que tenemos
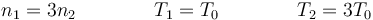
queda
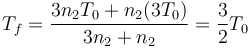
10.4 Pregunta 4
En el equilibrio final, ¿cómo es la fuerza sobre la pared central?
- A Apunta hacia la cámara 1.
- B Es nula.
- C Apunta hacia la cámara 2.
- D Puede apuntar en cualquiera de los dos sentidos, dependiendo del valor de T0.
- Solución
La respuesta correcta es la C
En el estado final, la presión de la cámara 1 cumple
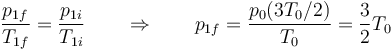
mientras que la de la cámara 2 verifica
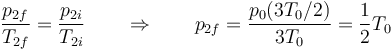
Al calentarse el gas de la cámara 1 aumenta su presión, mientras que al enfriarse el gas de la cámara 2 disminuye la suya. Por tanto en el estado final hay una fuerza que va de la cámara 1 (mayor presión) a la 2 (menor presión).
Esta fuerza debe ser resistida por la rigidez de la pared central. Si en lugar de una pared tuviéramos un émbolo, éste se desplazaría hasta que se alcanzara simultáneamente el equilibrio térmico y el mecánico.
11 Expansión adiabática y temperatura
En una expansión adiabática de un gas ideal, si T1 es su temperatura inicial y T2 es la final, ¿qué relación existe entre ellas?
- A T2 > T1.
- B T2 < T1.
- C T2 = T1.
- D Puede darse cualquiera de las otras tres situaciones, dependiendo de si el proceso es reversible o no.
- Solución
La respuesta correcta es la B.
En una expansión adiabática, el sistema realiza trabajo sobre el ambiente. Puesto que no entra calor en el sistema, este trabajo se realiza a costa de la energía interna, que por tanto disminuye. Si disminuye la energía interna del gas también lo hace su temperatura. Por tanto, la temperatura final es inferior a la inicial.
Este es el principio en que se basan muchos refrigeradores.
12 Masa que cuelga de una cámara de aire
Se tiene una balanza formada por un recipiente cilíndrico de 16 cm² de sección lleno de aire (considerado como un gas ideal). El tubo está cerrado herméticamente en su parte inferior por un émbolo que puede deslizarse sin rozamiento y que tiene un gancho en su cara inferior. Las paredes y el émbolo no están aislados térmicamente. Inicialmente el émbolo se encuentra a 15 cm de la pared superior, y el gas en equilibrio mecánico y térmico con el exterior, que se halla a 1 bar y 300 K. Se cuelga bruscamente del pistón un saco de harina de 4 kg.
12.1 Pregunta 1
¿Cuánto desciende aproximadamente el pistón hasta que se alcanza de nuevo el equilibrio?
- A 3 cm.
- B 5 cm.
- C 3 mm.
- D 0 cm.
- Solución
La respuesta correcta es la B.
La solución desarrollada aparece en el problema “Masa que cuelga de una cámara de aire”.
12.2 Pregunta 2
¿Cuánto vale aproximadamente el calor que entra en el sistema en este proceso?
- A +5.9 J
- B −6.7 J
- C 0 J
- D +6.7 J
- Solución
La respuesta correcta es la A.
La solución desarrollada aparece en el problema “Masa que cuelga de una cámara de aire”.
12.3 Pregunta 3
Suponga que el saco tiene un agujero, de forma que la harina se escapa lentamente hasta vaciarse por completo (despreciamos el peso del propio saco). ¿Cuánto vale el calor que entra en el sistema en este segundo proceso?
- A +5.9 J
- B −6.7 J
- C 0 J
- D +6.7 J
- Solución
La respuesta correcta es la B.
La solución desarrollada aparece en el problema “Masa que cuelga de una cámara de aire”.
Esta se puede resolver sin hacer cálculos, ya que en la compresión a temperatura constante entra trabajo en el sistema y sale calor, por lo que el calor que entra debe ser negativo.
13 Proceso de un gas diatómico
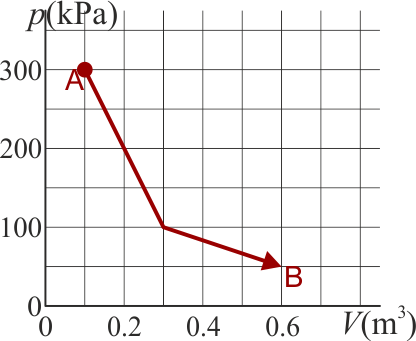
Un gas ideal diatómico experimenta un proceso cuasiestático desde un estado A a un estado B, según la gráfica de la figura
13.1 Pregunta 1
¿Cuánto es la variación de la energía interna del gas?
- A No podemos conocerlo sin saber el número de moles.
- B Es nula.
- C +62.5 kJ
- D −53.7 kJ
- Solución
La respuesta correcta es la B.
La variación en la energía interna es
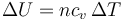
Si sustituimos la relación entre la capacidad calorífica molar y la constante de los gases ideales queda
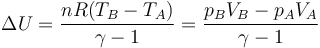
El valor numérico de esta cantidad es
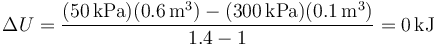
El estado final tiene la misma temperatura que el inicial y no hay variación en la energía interna.
13.2 Pregunta 2
¿Cuánto calor entra en el gas en este proceso?
- A −53.7 kJ
- B No podemos conocerlo sin saber el número de moles.
- C +62.5 kJ
- D +53.7 kJ
- Solución
La respuesta correcta es la C.
Calculamos el calor aplicando el primer principio de la termodinámica
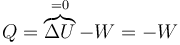
A su vez, el trabajo lo calculamos a partir de la integral de la presión

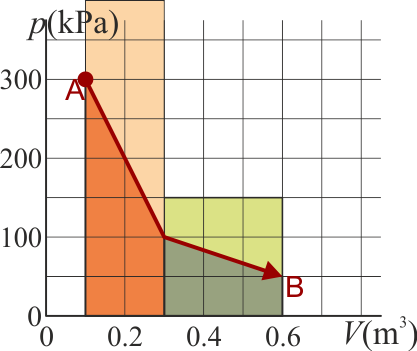
El área bajo la curva es la suma de dos trapecios. Su valor puede hallarse o bien aplicando la fórmula del área de un trapecio u observando que cada uno es la mitad de un rectángulo. Por ello
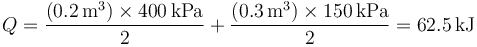
14 Aluminio sobre hielo
Un bloque de aluminio de 4 kg a 80 °C se coloca sobre un gran bloque de hielo a 0 °C. ¿Cuánto hielo se derrite, aproximadamente? (calor específico del aluminio: 0.897 kJ/(kg·K); calor específico del agua: 4.18 kJ/(kg·K); entalpía específica de fusión del agua: 333.55 kJ/kg)
- A 215 g
- B 4.0 kg
- C 860 g.
- D 11 g
- Solución
La respuesta correcta es la C.
El calor fluye del aluminio hacia el hielo, bajando su temperatura, hasta que llegue a 0°C. En ese momento se alcanza el equilibrio térmico con el hielo y deja de fluir calor. Como se nos dice que el bloque de hielo es grande, suponemos que el hielo no llega a agotarse, por lo que todo el calor del aluminio se emplea en fundir hielo.
El calor que sale del aluminio es
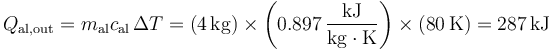
La masa de hielo que se funde es

Esta pregunta se puede hacer de forma sencilla por simple estimación. El calor específico es algo menos que la unidad, así que la cantidad de calor que sale es algo menos que 4×80 = 320 kJ. Como la entalpía específica de fusión son unos 340kJ por cada kilogramo, se derretirá algo menos de un kg. La única respuesta que cumple esto es la C.
15 Cámara que deja de estar aislada
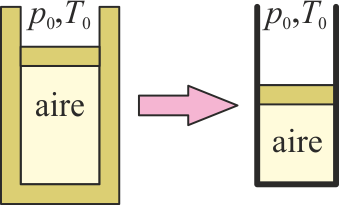
Se tiene una cierta cantidad de aire en un cilindro con paredes adiabáticas y con un pistón también adiabático, que puede moverse pero permanece en reposo, situado en un ambiente a presión p0 y temperatura T0. Al retirar el aislamiento térmico del cilindro, se encuentra que el pistón comprime el gas.
15.1 Pregunta 1
Antes de retirar el aislamiento, ¿había equilibrio entre el aire y el ambiente?
- A Había equilibrio tanto térmico como mecánico.
- B No había equilibrio ni térmico ni mecánico.
- C Había equilibrio mecánico, pero no térmico.
- D Había equilibrio térmico, pero no mecánico.
- Solución
La respuesta correcta es la C.
Puesto que el pistón puede moverse pero no lo hace, existe equilibrio mecánico. Por otra parte, al retirar el aislante térmico el sistema evoluciona, lo que indica que antes de retirarlo no existía equilibrio térmico.
15.2 Pregunta 2
¿Qué podemos decir de la temperatura inicial del gas, Ti?
- A No podemos saber nada de la temperatura inicial.
- B Ti = T0
- C Ti > T0
- D Ti < T0
- Solución
La respuesta correcta es la C.
La presión en el instante inicial y el final es la misma, ya que hay equilibrio mecánico con el ambiente. Por tanto se cumple la ley de Charles
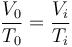
o, lo que es lo mismo,
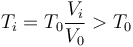
A presión constante, si el volumen se reduce es porque el gas se enfría. Por tanto, su temperatura inicial era superior a la final.
16 Otro proceso sobre un gas
Un gas ideal diatómico ocupa un cierto volumen V0 a una presión p0 y una temperatura T0. Primero, manteniendo constante su volumen, se reduce lentamente su presión a p0 / 2. Luego, manteniendo constante su nueva presión, se pone gradualmente en contacto con un foco a temperatura T0
16.1 Pregunta 1
¿Como se relacionan el volumen inicial, V0, y final Vf, del gas?
- A Vf = V0
- B Vf = V0 / 2
- C Vf = 2V0
- D Vf = 4V0
- Solución
La respuesta correcta es la C.
En el estado final la temperatura es la misma que la inicial, por lo que se cumple la ley de Boyle
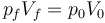
Puesto que la presión se reduce a la mitad, el volumen aumenta al doble
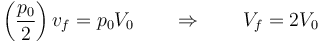
16.2 Pregunta 2
¿Cuánto trabajo intercambia el gas en este proceso?
- A Win = p0V0 / 2
- B Wout = p0V0 / 2
- C Win = p0V0
- D Wout = p0V0
- Solución
La respuesta correcta es la B.
El primer proceso es uno a volumen constante, por lo que en él no se realiza trabajo. El segundo es a presión constante, por lo que el trabajo corresponde al área de un rectángulo
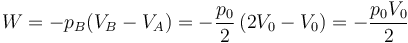
Es negativo porque se trata de una expansión y es el gas el que trabaja sobre el ambiente. En términos de trabajo que entra o trabajo que sale sería
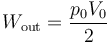
17 Proceso de un gas ideal
Un gas ideal diatómico ocupa inicialmente un volumen de 0.2 m³ a 1 bar y 300 K. Se comprime cuasiestáticamente hasta que su volumen es 0.1 m³ según el proceso (p en bares, V en m³)
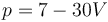
17.1 Pregunta 1
Para este proceso, ¿cuánto trabajo se realiza sobre el gas?
- A +20 kJ
- B −0.25 J.
- C +25 kJ
- D −25 kJ
- Solución
La respuesta correcta es la C.
Por tratarse de un proceso cuasiestático, el trabajo puede calcularse integrando la presión interna
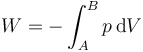
En este caso, midiendo la presión en bares y el volumen en metros cúbicos
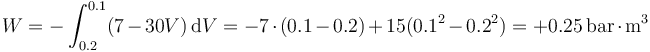
siendo
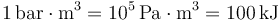
queda
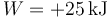
17.2 Pregunta 2
¿Cuánto varía su energía interna?
- A +0.20 J
- B +25 kJ
- C +50 kJ
- D −50 kJ
- Solución
La respuesta correcta es la C.
Para un gas ideal, la variación de la energía interna entre dos estados (cuando cv es constante) se puede calcular como
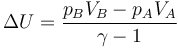
En el estado inicial tenemos

y en el final
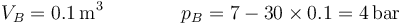
Esto nos da una variación en la energía interna
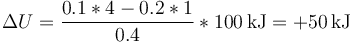
Asimismo, el primer principio de la termodinámica nos dice que en este proceso entra un calor
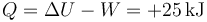
18 Flujo de calor en esfera
Un recipiente esférico de vidrio (con conductividad térmica 0.96 W/m·K) de 10 cm de radio y 2 mm de espesor está lleno de agua a 10 °C, estando el aire exterior a 20 °C. ¿Cuánto vale el flujo de calor que entra en la esfera?
- A +201 W
- B +480 W
- C +603 W
- D −201 W
- Solución
La respuesta correcta es la C.
El flujo de calor a través de una lámina sólida lo da la ley de Fourier
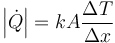
siendo la resistencia térmica en este caso
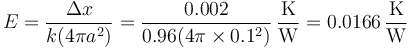
y el flujo de calor

19 Calor que atraviesa una ventana
Una ventana aislante está formada por un vidrio ( ) de 5 mm de espesor, una capa de aire (
) de 5 mm de espesor, una capa de aire (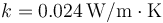 ) de 2 cm y otro vidrio de 5 mm. ¿Cuánto vale la resistencia térmica de 1 m² de ventana?
) de 2 cm y otro vidrio de 5 mm. ¿Cuánto vale la resistencia térmica de 1 m² de ventana?
- A 385 K/W
- B 1.19 K/W
- C 2.60 mK/W
- D 0.84 K/W
- Solución
La respuesta correcta es la D.
La resistencia térmica de una lámina es igual a
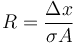
Si tenemos varias capas en serie las resistencias se suman

En este caso, puesto que la capa de aire es más gruesa y además conduce mucho peor el calor, la principal contribución a la resistencia total vendrá de la capa de aire, por lo que podemos aproximar
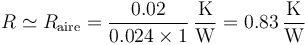
de lo cual ya tenemos la respuesta correcta.
Un cálculo exacto, incluyendo las tres capas da
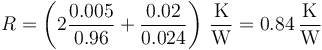
20 Variación del calor por radiación
Se calienta un trozo de metal de 300 K a 900 K. ¿Cómo cambia la cantidad de calor que escapa del metal por radiación?
- A Se multiplica por 3.
- B Se divide por 3.
- C Se multiplica por 9.
- D Se multiplica por 81.
- Solución
La respuesta correcta es la D.
El calor radiado cumple la ley de Stefan-Boltzmannn
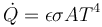
donde lo relevante en este caso es que depende como la cuarta potencia de la temperatura. Por tanto, si esta se multiplica por 3, el flujo de calor radiado se multiplica por 34 = 81.





