Energía y leyes de conservación (GIOI)
De Laplace
Constantes de movimiento
Una constante de movimiento (también llamada integral primera) es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una) cuyo valor es constante, pese a que la posición y la velocidad sí son variables en el tiempo
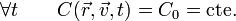
Por ejemplo, supongamos una partícula que describe el movimiento circular
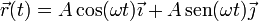
Este movimiento verifica las relaciones
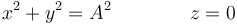
Así, aunque tanto x como y son funciones del tiempo, una combinación de las dos coordenadas permanece constante. Si hubiéramos conocido esta constancia antes de determinar la ley horaria, sabríamos que la trayectoria es una circunferencia, aunque la rapidez pudiera ser desconocida.
El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posición y velocidad en cualquier instante)
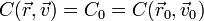
El ejemplo más conocido de constante de movimiento, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.
Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. A continuación estudiaremos tres magnitudes, construidas a partir de la posición y la velocidad, cuyas leyes de evolución pueden determinarse a partir de las leyes de Newton. Estas cantidades, si se dan las condiciones adecuadas, son constantes de movimiento, y por tanto son las primeras candidatas cuando en un problema se buscan integrales primeras. Estas magnitudes son:





