Cálculo de aceleración en una curva
De Laplace
Contenido |
1 Enunciado
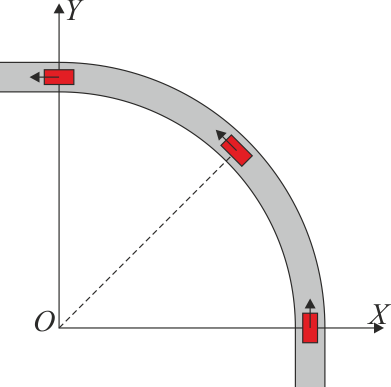
Un coche entra en una curva de 90° y 100 m de radio a 80 km/h. Disminuye su rapidez uniformemente hasta salir de la curva a 50 km/h.
- Determine su rapidez cuando ha recorrido 1/3 de la curva, la mitad y 2/3 de ella.
- Halle su aceleración tangencial y su aceleración normal en los mismos puntos.
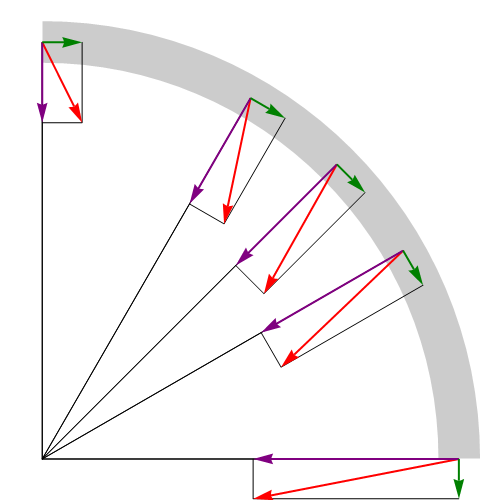
- Exprese el vector aceleración en estos puntos en los ejes indicados en la figura
2 Rapidez
Como en el problema de la aceleración en una recta podría parecer que la rapidez varía linealmente con la posición y por tanto, a mitad de la curva la velocidad se habrá reducido en un 50% de la variación total. Sin embargo, no es así. Lo que es constante en este problema es la derivada respecto al tiempo, no la derivada respecto a la posición.
Se nos dice que
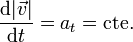
aunque no se nos dice cuánto vale esta cantidad, solo la velocidad en dos puntos conocidos (80 km/h a la entrada y 50 km/h a la salida).
El cálculo es análogo al caso rectilíneo, pero empleando la rapidez y la distancia recorrida en lugar de la velocidad y la posición. Tenemos por un lado que, al ser constante
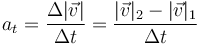
mientras que la rapidez media es la media de la rapidez inicial y la final

Si multiplicamos estas dos ecuaciones
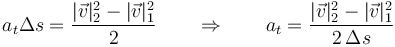
siendo la distancia recorrida
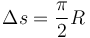
A este resultado se puede llegar también despejando de las ecuaciones del movimiento uniformemente acelerado para el movimiento a lo largo de la carretera
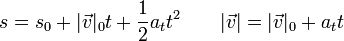
El valor resultante de la aceleración tangencial es, pasando las velocidades a m/s,
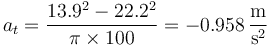
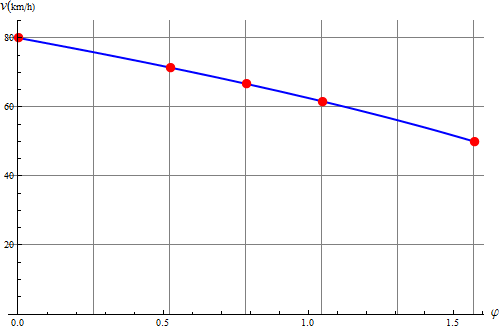
Para los puntos intermedios aplicamos la relación correspondiente para un cierto ángulo θ
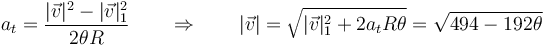
Aplicando esta fórmula a los valores indicados nos queda la tabla
| θ | 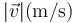
| 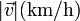
|
|---|---|---|
| 0 | 22.2 | 80.0 |
| π/6 | 19.8 | 71.4 |
| π/4 | 18.5 | 66.7 |
| π/3 | 17.1 | 61.6 |
| π/2 | 13.9 | 50.0 |
3 Componentes intrínsecas de la aceleración
3.1 Aceleración tangencial
La aceleración tangencial, según indica el enunciado, es constante, y su expresión y valor ya lo hemos calculado en el apartado anterior

3.2 Aceleración normal
La aceleración normal, en cada punto de la curva, tiene la expresión
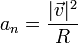
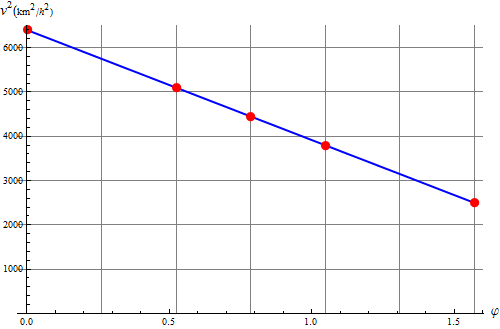
puesto que el radio de curvatura es constante y el cuadrado de la rapidez varía linealmente con la distancia, esta aceleración normal es también una función lineal del ángulo
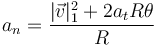
Sustituyendo los valores del enunciado (pasados a metros por segundo) queda
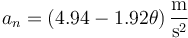
Esto nos da la siguiente tabla de valores
| θ | at(m / s2) | an(m / s2) |
|---|---|---|
| 0 | -0.958 | 4.94 |
| π/6 | -0.958 | 3.94 |
| π/4 | -0.958 | 3.43 |
| π/3 | -0.958 | 2.93 |
| π/2 | -0.958 | 1.93 |
4 Vector aceleración
Una vez que tenemos las componentes intrínsecas, construimos el vector aceleración como
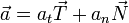
Aquí  es el vector unitario tangente a la trayectoria, en la dirección y sentido de la velocidad. En función del ángulo θ este unitario es igual a
es el vector unitario tangente a la trayectoria, en la dirección y sentido de la velocidad. En función del ángulo θ este unitario es igual a
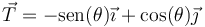
mientras que el vector normal es el unitario hacia adentro de la circunferencia
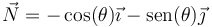
Combinando los dos términos nos queda el vector aceleración
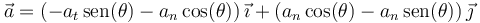
Sustituyendo los valores de los ángulos del enunciado
| θ | 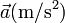
|
|---|---|
| 0 | 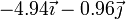
|
| π/6 | 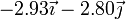
|
| π/4 | 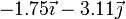
|
| π/3 | 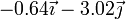
|
| π/2 | 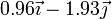
|