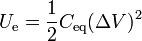Condensadores (GIOI)
De Laplace
Contenido |
1 Condensadores
1.1 Definición
Cuando tenemos un sistema de conductores separados por el vacío (o por un dieléctrico) y se fijan sus potenciales, habrá líneas de campo que vayan de uno a otro y también las habrá que vayan o vengan del infinito. En este sistema se almacena carga en cada conductor (que será positiva en algunos y negativa en otros). El sistema almacena igualmente una energía electrostática, que podemos situar en el campo eléctrico o en las cargas.
Podemos simplificar el estudio de la carga y la energía almacenada reduciendo el problema a partes más sencillas. Para ello nos centramos en lo que ocurre en cada par de conductores.
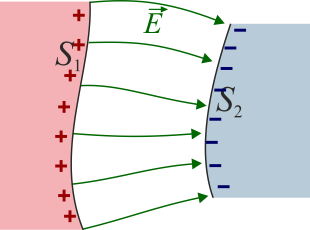
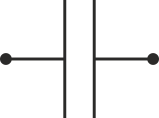
Dos superficies conductoras S1 y S2 están en influencia total cuando todas las líneas de campo que salen de una van a parar a la otra. Cuando tenemos dos superficies conductoras en influencia total se dice que tenemos un condensador y a las dos superficies se las conoce como las placas o armaduras del condensador. Su símbolo en teoría de circuitos está formado por dos líneas paralelas.
Una de las superficies tendrá carga positiva y la otra negativa. dado que el número de líneas de campo que salen de una van a parar a la otra, las dos cargas son iguales y opuestas.
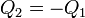
Esto quiere decir que un condensador no almacena carga neta, ya que esta siempre es cero. Cuando se dice que un condensador almacena tal o cual carga o se encuentra cargado, se refiere siempre a la carga de la placa positiva.
Lo que sí almacena un condensador es energía eléctrica, por el campo eléctrico que hay entre las placas
1.2 Capacidad de un condensador
Cuando tenemos un condensador cargado, existe un campo eléctrico que va de la placa positiva a la negativa. Por tanto, habrá una diferencia de potencial entre ambas placas
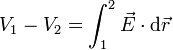
Esta d.d.p. es proporcional a la carga de las placas. Cuanto mayor sea la carga, mayor el campo y mayor la d.d.p. por lo que se puede escribir la relación
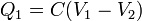
siendo C la capacidad del condensador. Puede definirse mediante la relación
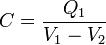
es decir, la capacidad de un condensador es igual al cociente entre la carga de una placa y la diferencia de potencial entre esa placa y la otra. Podemos tomar la placa que queramos como referencia, no necesariamente la positiva, ya que
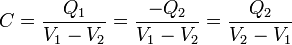
La capacidad de un condensador se mide en faradios (F) con 1 F = 1 C/1 V. Esta unidad, no obstante, es demasiado grande para las capacidades usuales, que se miden en picofaradios (1pF = 10−12F), nanofaradios (1nF = 10−9F) y microfaradios (1μF = 10−6F)
A pesar de que en la definición aparecen la carga y la diferencia de potencial, la capacidad de un condensador es una propiedad geométrica, que depende de la forma y distancia de las superficies, así como de los materiales interpuestos, pero no de a qué tensión se encuentran.
Aunque son conceptos similares, no es lo mismo la capacidad de un conductor que se refiere a la carga de un conductor en completa soledad, con la capacidad de un condensador, que relaciona dos superficies enfrentadas.
1.2.1 Condensador plano
El caso más sencillo de condensador, y el más utilizado como modelo, es el condensador plano formado por dos placas conductoras planas y paralelas, de área S y situadas a una distancia a a la una de la otra.
Una de las placas almacena una carga + Q y la otra una − Q. En un sistema real, el campo va de una placa a la otra, con líneas de campo que pueden ser curvadas
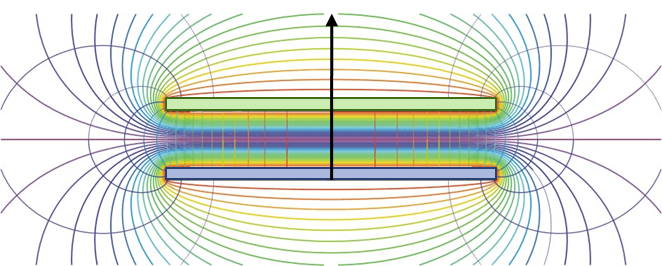
Sin embargo, si las placas están muy próximas, puede despreciarse el efecto de esas líneas exteriores (lo que se llaman los efectos de borde) y aproximar el campo entre las placas como uno entre dos planos paralelos de gran extensión.
En ese caso, la densidad de carga en cada placa es uniforme
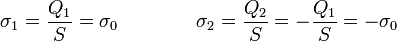
y, tal como se ve en un problema, el campo vale lo mismo en todos los puntos entre las placas
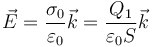
por lo que la diferencia de potencial entre las placas vale
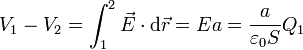
lo que nos da la capacidad
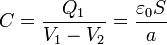
Vemos que el resultado no depende de la carga de las placas, sino del material interpuesto (vacío en este caso), el área de las placas (sin importar si son cuadradas, circulares o de otra forma) y la distancia entre ellas.
1.2.2 Condensador esférico
Un condensador esférico está formado por dos superficies esféricas concéntricas, de radios a y b. La esfera interior almacena una carga Q1 y la superficie esférica del hueco una Q2 = − Q1. Tal como se ve al estudiar el problema de dos esferas concéntricas con cargas 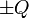 la diferencia de potencial entre ellas es
la diferencia de potencial entre ellas es
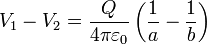
lo que nos da la capacidad
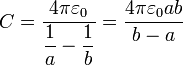
Este resultado contiene como caso particular la capacidad de un conductor esférico. Si consideramos una esfera en ausencia de más conductores, como un condensador una de cuyas placas es la propia esfera y la otra es la tierra, situada en el infinito, la capacidad equivale a tomar el límite 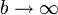
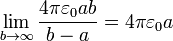
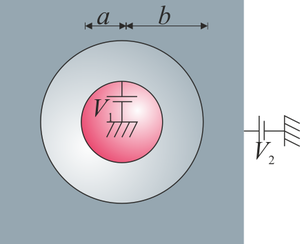
1.2.3 Condensador coaxial
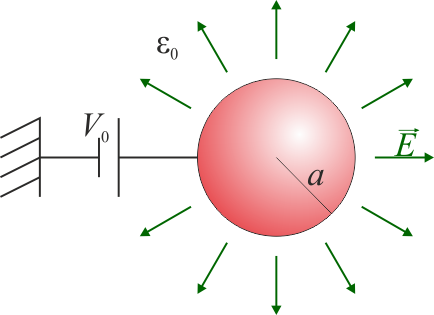
Otro tipo común de condensador es el coaxial, formado por dos cilindros concéntricos, como en los cables de antena de un televisor, ilustrados más arriba. Para una porción de longitud h de un cable de este tipo, con radio interior a y exterior b, la capacidad vale
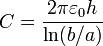
1.3 Circuitos equivalentes
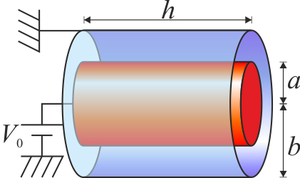
Una vez que se ha definido lo que es un condensador, su extensión es inmediata a cualquier sistema de conductores.

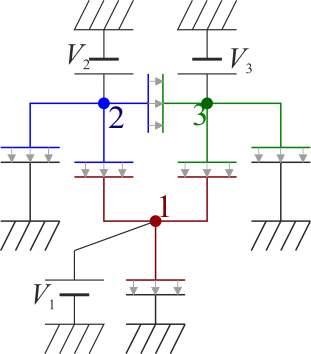
Cuando tenemos un conjunto de conductores, habrá líneas de campo que vaya de uno a otro y líneas que vayan al infinito. Construimos entonces un circuito en el que:
- Cada conductor es representado por un nodo (“1”, “2”,…)
- Hay un condensador entre cada par de nodos, que representa la influencia entre dos conductores.
- Hay un condensador entre cada nodo y tierra, que representa las líneas que van o vienen del infinito.
- Hay una fuente de tensión ideal que fija el voltaje de cada conductor.
1.4 Asociaciones de condensadores
De entre los posibles sistemas de condensadores, existen dos asociaciones que son especialmente importante, ya que permiten reducir un conjunto de condensadores a un solo elemento con una capacidad equivalente a toda la asociación.
1.4.1 Condensadores en paralelo
Dos condensadores están en paralelo cuando están conectados por sus dos extremos, de forma que la diferencia de potencial entre placas es la misma para los dos
La carga almacenada en la placa positiva de cada condensador será diferente en cada caso
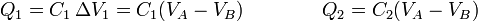
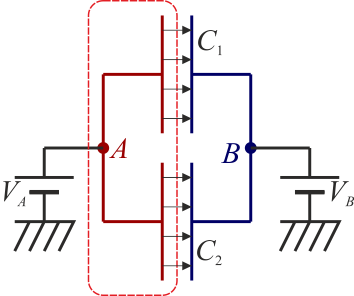
La carga almacenada en el conductor A es la de todos los condensadores unidos al nodo correspondiente
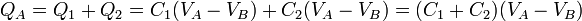
Por tanto, la asociación es equivalente a un solo condensador de capacidad la suma de las dos individuales
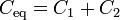
1.4.2 Condensadores en serie
Dos condensadores están en serie cuando están conectados por uno de sus extremos, y el nodo de conexión está aislado y descargado (gráficamente, si en el nodo de conexión no hay ninguna otra rama unida a una fuente u otro condensador).
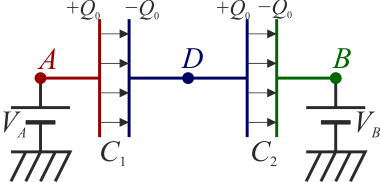
En este caso, si el primer condensador tiene una carga Q1 = Q0 en su placa positiva, tendrá una carga − Q0 en la negativa. Ahora bien, por ser el conductor central uno aislado y descargado, esta carga solo puede provenir del propio conductor, por lo que en la placa positiva del segundo condensador habrá una carga
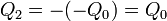
es decir, la carga en la placa positiva de ambos condensadores es la misma. La diferencia de potencial en cada uno es diferente. Si D es el punto central

La diferencia de potencial total de la asociación es la suma de estas dos
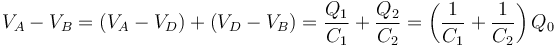
Puesto que el condensador equivalente cumple
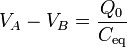
llegamos a
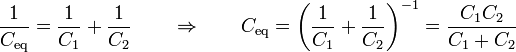
La capacidad equivalente a dos condensadores en serie es menor que cualquiera de ellas. Por ejemplo, para un condensador de 3 nF, puesto en serie con uno de 6 nF
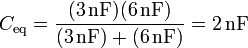
Podemos preguntarnos para qué sirve entonces asociar condensadores en serie. Aparte de que puede ocurrir que aparezcan de manera natural en el modelado de un sistema, pueden diseñarse de esta forma si lo que se desea es soportar una elevada diferencia de potencial. Si por ejemplo, tenemos una línea de alta tensión a 20kV, cuyo cable pasa por una torre, que está a tierra, el aislador que impide la descarga está formado por una serie de condensadores puestos en serie.

1.4.3 Combinación de asociaciones
Las asociaciones de condensadores en serie y en paralelo pueden asociarse a su vez, entre sí, reduciendo una red compleja a un conjunto mínimo de condensadores equivalentes.
Así, por ejemplo, la estructura
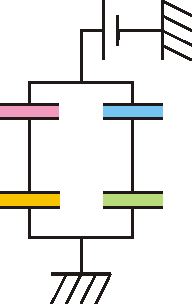
es una asociación en paralelo de dos asociaciones en serie. Para hallar la capacidad equivalente, primero se asocian cada uno de los pares en serie y luego el conjunto de dos en paralelo, tal como se ve en un problema.
Este sistema:
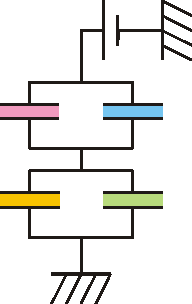
es una asociación en serie de dos asociaciones en paralelo. Para reducirlo a uno solo se opera de forma análoga.
A la hora de identificar asociaciones en serie y en paralelo no hay que dejarse engañar por la disposición en el dibujo. Así, estos dos condensadores están en serie
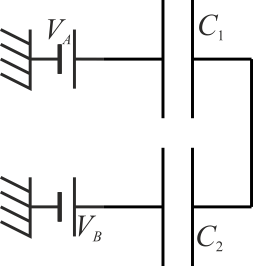
y estos dos en paralelo
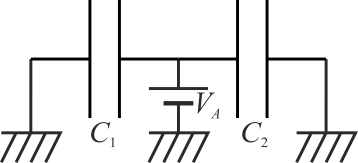
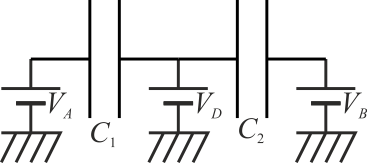
y estos, ni en serie ni en paralelo:
2 Energía en un sistema de conductores
Antes hemos dicho que en un sistema de conductores o en el equivalente circuito de condensadores se almacena energía eléctrica, porque las cargas se encuentran a cierto potencial o porque hay un campo eléctrico entre los conductores (ambas descripciones son equivalentes).
Consideraremos solo el caso de que toda la carga esté sobre los conductores y no en el espacio entre ellas. En este caso es de aplicación la fórmula para la energía de una distribución
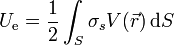
ya que toda la carga está en la superficie de los conductores. En esta expresión el potencial es función de la posición, ya que tendrá un valor diferente para cada uno de los conductores del sistema. Esta integral sobre todas las superficies la podemos descomponer en una suma de integrales sobre cada uno de los conductores
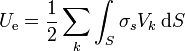
con la ventaja de que ahora el potencial en cada uno de los conductores tiene un solo valor, por lo que puede salir de cada integral
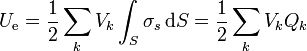
es decir, la energía solo depende de los potenciales de los diferentes conductores y de cuanto vale la carga total en cada uno de ellos, pero no de como está distribuida sobre la superficie.
Puesto que de antemano no se conocen simultáneamente la carga y el potencial de cada conductor (o una cosa o la otra), la energía solo se puede hallar una vez que se ha resuelto el problema del potencial y calculado las cantidades desconocidas.
En el caso particular de una sola esfera con carga Q su potencial vale
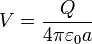
y por tanto su energía es
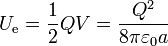
¿Cuánta energía hace falta para colocar una carga de 1 C es una esfera de 1 m de radio? Por simple sustitución obtenemos
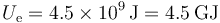
que es una cantidad gigantesca de energía, lo cual muestra la dificultad de concentrar una cantidad tan grande de carga.

Es más, si se calcula la presión a la que estaría sometida la esfera debida a a las fuerzas eléctricas, se obtiene un valor de 3500 bares (0.35 GPa), lo cual supera la resistencia de cualquier material conocido.
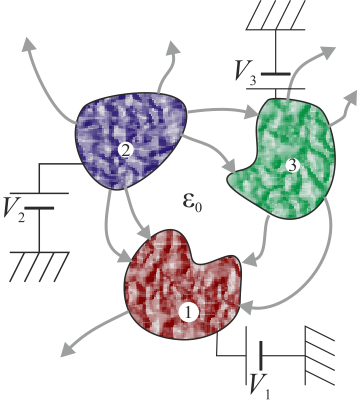
2.1 Energía de un condensador
En el caso particular de un condensador, tenemos dos superficies conductoras con cargas iguales y opuestas y una d.d.p. entre ellas. La energía almacenada en el condensador vale
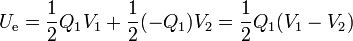
es decir, es igual a la carga del condensador (la de una se sus placas) multiplicada por la diferencia de potencial entre esa placa y la otra.
En función de la capacidad
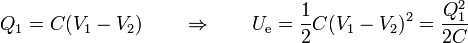
Así, para un condensador plano queda
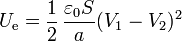
Podemos ver que se llega al mismo resultado a partir del campo eléctrico. En el caso de un condensador plano, el campo eléctrico es igual a
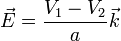
La densidad de energía eléctrica dentro del condensador
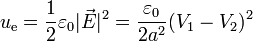
y la energía total almacenada en él, teniendo en cuenta que el volumen equivale al área de las placas multiplicada por la distancia entre ellas
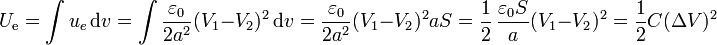
Concluimos entonces que un condensador es un dispositivo que almacena energía eléctrica por tener un campo eléctrico entre sus placas.
En el caso de que tengamos un sistema de condensadores, la energía total será la suma de la energía almacenada en cada uno
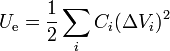
En particular, tanto para una asociación en serie como para una en paralelo la energía total es igual a la que almacenaría el condensador equivalente