Casos particulares de movimiento tridimensional (GIOI)

De Laplace

1 Rectilíneo

1.1 Caracterización

Un movimiento rectilíneo, como su nombre indica, es aquel cuya trayectoria es una recta (o un segmento).

Existen diferentes formas de caracterizar un movimiento rectilíneo

La trayectoria es una recta: Esto se puede expresar diciendo que existen dos vectores constantes, $\vec{A}$ , $\vec{u}$ tales que

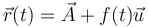
$\vec{r}(t) = \vec{A}+f(t)\vec{u}$

Esta expresión constituye una ecuación paramétrica de una recta.

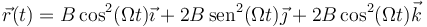
Así, por ejemplo, el movimiento $\vec{r}(t)=B\cos^2(\Omega t)\vec{\imath}+2B\,\mathrm{sen}^2(\Omega t)\vec{\jmath}+2B\cos^2(\Omega t)\vec{k}\,$

puede escribirse, usando la identidad fundamental de la trigonometría, como

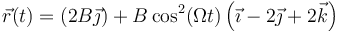
$\vec{r}(t) = \left(2B\vec{\jmath}\right)+B\cos^2(\Omega t)\left(\vec{\imath}-2\vec{\jmath}+2\vec{k}\right)\,$

La trayectoria está en la intersección de dos planos: Una recta puede definirse como la intersección de dos planos. por tanto, si encontramos vectores constantes 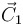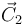$\vec{C}_1$ , $\vec{C}_2$ y escalares $k 1$ y $k 2$ tales que

$\vec{C}_1\cdot\vec{r}=k_1\qquad\qquad \vec{C}_2\cdot\vec{r}=k_2$

entonces la trayectoria es una recta.

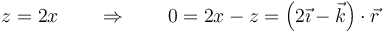
Así, para el ejemplo anterior se cumple $z = 2x \qquad\Rightarrow\qquad 0 = 2x-z = \left(2\vec{\imath}-\vec{k}\right)\cdot\vec{r}$

y

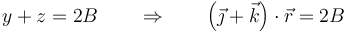
$y+z = 2B \qquad\Rightarrow\qquad \left(\vec{\jmath}+\vec{k}\right)\cdot\vec{r}=2B$

La dirección del vector tangente permanece constante: Esto implica que, una vez calculado el vector tangente, este permanece constante, o como mucho cambia de sentido.

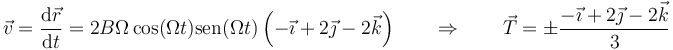
Así, para nuestro ejemplo $\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=2B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)\qquad \Rightarrow\qquad \vec{T}=\pm\frac{-\vec{\imath}+2\vec{\jmath}-2\vec{k}}{3}$

La aceleración normal es nula: $a n$ rd responsable del cambio de dirección en la velocidad, es siempre nula. La velocidad y la aceleración son siempre paralelas en un movimiento rectilíneo

$\mbox{Movimiento rectilineo}\qquad \Leftrightarrow \qquad\vec{T}=\mathrm{cte}\qquad \Leftrightarrow \qquad \vec{a}_n=\vec{0}\qquad \Leftrightarrow \qquad \vec{v}\times\vec{a}=\vec{0}\quad\forall t$

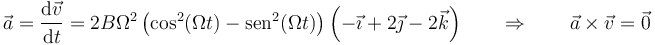
Siguiendo con nuestro ejemplo $\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=2B\Omega^2\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)\qquad \Rightarrow\qquad \vec{a}\times\vec{v}=\vec{0}$

El radio de curvatura tiende a infinito: Una recta se puede considerar como una circunferencia de radio infinito.

En el caso de un movimiento rectilíneo, el parámetro arco no es más que la distancia medida sobre la recta en que se desplaza la partícula, de forma que la posición, velocidad y aceleración en cualquier instante se pueden escribir como

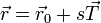
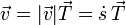
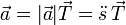
$\vec{r}=\vec{r}_0 + s\vec{T}$ $\vec{v}=|\vec{v}|\vec{T}=\dot{s}\,\vec{T}$ $\vec{a}=|\vec{a}|\vec{T}=\ddot{s}\,\vec{T}$

Puesto que la elección de ejes de coordenadas es arbitraria, si estamos estudiando el movimiento rectilíneo de una sola partícula, podemos tomar el eje X como la recta soporte del movimiento y reducir la descripción a una escalar

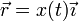
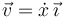
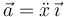
$\vec{r}=x(t)\vec{\imath}$ $\vec{v}=\dot{x}\,\vec{\imath}$ $\vec{a}=\ddot{x}\,\vec{\imath}$

1.2 Rectilíneo y uniforme

Un caso particular importante es el del movimiento con aceleración nula

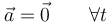
$\vec{a}=\vec{0}\qquad\forall t$

En este caso la velocidad es un vector constante

$\vec{v}=\vec{v}_0=\mathrm{cte}$

y por tanto el vector tangente, que marca la dirección, también lo es. Luego el movimiento es rectilíneo. Como además la rapidez es constante, también es uniforme. Luego todo movmiento con aceleración nula es rectilíneo y uniforme

Integrando otra vez obtenemos la posición

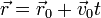
$\vec{r}=\vec{r}_0+\vec{v}_0t$

que es un caso particular de ecuaciones paramétricas de una recta.

1.3 Rectilíneo uniformemente acelerado

Otro caso particular de movimiento rectilíneo es aquel en que la aceleración es una constante y la velocidad inicial es paralela a ella

$\vec{a}=a_0\vec{u}\qquad\qquad \vec{v}=v_0\vec{u}$

con $\vec{u}$ un vector constante. En este caso, la velocidad en cualquier otro instante será

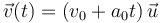
$\vec{v}(t) =\left(v_0+a_0t\right)\vec{u}$

En este movimiento la posición varía de forma cuadrática con el tiempo

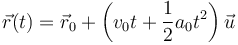
$\vec{r}(t) = \vec{r}_0+\left(v_0t+\frac{1}{2}a_0t^2\right)\vec{u}$

2 Movimiento plano

Dentro de los movimientos generales, un subconjunto muy importante es el de los movimientos planos, definidos por la condición de que la velocidad y la aceleración estén siempre contenidas en el mismo plano.

2.1 Caracterización del movimiento plano

En un movimiento en un plano, éste no tiene por qué ser uno de los planos coordenados, por lo que el criterio de que en el vector de posición aparezcan solo dos coordenadas ( $x$ e $y$ , por ejemplo) no es suficiente para establecer que el movimiento sea plano.

Para caracteriza cuándo un movimiento es plano tenemos varias técnicas equivalentes:

El vector de posición evoluciona en solo dos dimensiones: por tanto, el vector de posición es combinación lineal de dos vectores constantes

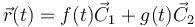
$\vec{r}(t)=f(t)\vec{C}_1+g(t)\vec{C}_2$

Un caso particular muy usual es aquél en que los dos vectores pertenecen a la base cartesiana.

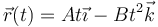
Así, la ecuación horaria $\vec{r}(t) = At \vec{\imath}-Bt^2\vec{k}$

corresponde a un movimiento plano. Un caso más general sería, por ejemplo,

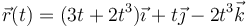
$\vec{r}(t)=(3t+2t^3)\vec{\imath}+t\vec{\jmath}-2t^3\vec{k}$

que no es evidente que se trata de un movimiento plano hasta que lo escribimos como

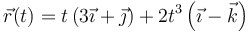
$\vec{r}(t)=t\left(3\vec{\imath}+\vec{\jmath}\right)+2t^3\left(\vec{\imath}-\vec{k}\right)$ que es una combinación lineal de dos vectores constantes.

La trayectoria está contenida en un plano: Es decir, existe un vector constante $\vec{B}$ y una constante $k$ tal que en todo momento

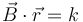
$\vec{B}\cdot\vec{r}=k$

Muchas veces, el vector $\vec{B}$ puede hallarse por simple inspección.

Otra forma de escribir esto mismo es hallar 4 constantes tales que, para todo instante

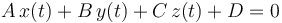
$A\,x(t) + B\,y(t)+C\,z(t) + D = 0$

siendo A,B,C las componentes del vector $\vec{B}$ .

Así para el ejemplo anterior se cumple que $\left\{\begin{array}{rcl}x & = & 3t+2t^3 \\ y & = & t \\ z & = & -2t^3\end{array}\right.\qquad\Rightarrow\qquad x = 3y-z\qquad\Rightarrow\qquad x - 3y + z = 0$

El vector velocidad y el vector aceleración definen un plano: Se trata de que este plano siempre sea el mismo. Para ello el vector binormal, unitario perpendicular al plano

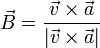
$\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}$

debe ser independiente del tiempo. A partir de la velocidad y la aceleración se halla $\vec{B}$ . Si es evidente que es constante, o su derivada respecto al tiempo es nula en todo momento, entonces el movimiento es plano.

$\vec{B}\neq \vec{B}(t) \qquad \Leftrightarrow\qquad \mbox{movimiento plano}$

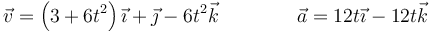
Siguiendo con el mismo ejemplo $\vec{v}=\left(3+6t^2\right)\vec{\imath}+\vec{\jmath}-6t^2\vec{k}\qquad\qquad \vec{a}=12t\vec{\imath}-12t\vec{k}$

Siendo el unitario de su producto vectorial

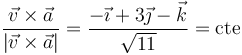
$\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}=\frac{-\vec{\imath}+3\vec{\jmath}-\vec{k}}{\sqrt{11}}=\mathrm{cte}$

Equivalentemente, en lugar de la velocidad y la aceleración pueden emplearse los vectores tangente y normal.

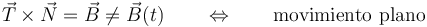
$\vec{T}\times \vec{N} = \vec{B} \neq \vec{B}(t) \qquad \Leftrightarrow\qquad \mbox{movimiento plano}$

La derivada de la aceleración está en el mismo plano que la velocidad y la aceleración: Otra forma consiste en observar que, puesto que la velocidad y la aceleración deben estar siempre en el mismo plano, la derivada respecto al tiempo de la aceleración (que nos da cómo varía ésta) también debe encontrarse en el mismo plano. Por tanto, debe ser ortogonal al vector $\vec{B}$ definido anteriormente. Esto nos lleva a la condición vectorial

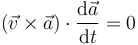
$(\vec{v}\times\vec{a})\cdot\frac{\mathrm{d}\vec{a}}{\mathrm{d}t} = 0$

En términos de las componentes cartesianas, esta condición se puede escribir

$\left|\begin{matrix} v_x & v_y & v_z \\ a_x & a_y & a_z \\ \dot{a}_x & \dot{a}_y & \dot{a}_z\end{matrix}\right| = 0 \qquad \Leftrightarrow\qquad \mbox{movimiento plano}$

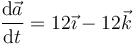
En nuestro caso, hallamos la derivada de la aceleración respecto al tiempo $\frac{\mathrm{d}\vec{a}}{\mathrm{d}t} = 12 \vec{\imath}-12\vec{k}$

Construimos el determinante con los tres vectores

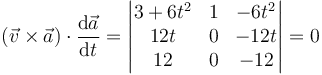
$(\vec{v}\times\vec{a})\cdot\frac{\mathrm{d}\vec{a}}{\mathrm{d}t} = \left|\begin{matrix} 3+6t^2 & 1 & -6t^2 \\ 12t & 0 & -12t \\ 12 & 0 & -12\end{matrix}\right| = 0$ Puesto que la segunda y la tercera fila son proporcionales, el determinante es nulo. Por tanto, el movimiento es plano, aunque no lo pareciera en principio.

2.2 Coordenadas cartesianas

En el caso del movimiento plano, puede elegirse un sistema de referencia en el que el plano de movimiento sea el OXY. En este caso, la posición, la velocidad y la aceleración pueden escribirse como vectores de solo dos componentes

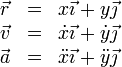
$\begin{array}{ccc} \vec{r} & = & x\vec{\imath}+y\vec{\jmath}\\ \vec{v} & = & \dot{x}\vec{\imath}+\dot{y}\vec{\jmath}\\ \vec{a} & = & \ddot{x}\vec{\imath}+\ddot{y}\vec{\jmath}\\ \end{array}$

2.3 Coordenadas polares

En el caso de movimiento en un plano, es útil considerar las coordenadas polares para describir el movimiento de la partícula, ${ρ,θ}$ . Estas coordenadas son la distancia al origen del sistema de referencia $(ρ)$ y el ángulo que forma el vector de posición con el eje $O X$ $(θ)$ .

$x = \rho\cos(\theta) \qquad y = \rho\,\mathrm{sen}(\theta)$

y sus inversas

$\rho = \sqrt{x^2+y^2}\qquad \theta=\mathrm{arctg}\left(\frac{y}{x}\right)$

Las coordenadas polares llevan asociadas una base vectorial 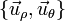$\{\vec{u}_{\rho},\vec{u}_{\theta}\}$ , que apuntan respectivamente en la dirección radial (en la que varía $ρ$ ) y acimutal (en la que varía $θ$ ). Esta base se relaciona con la canónica por el cambio de base

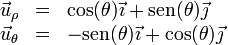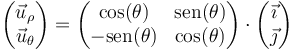
$\begin{array}{rcl} \vec{u}_\rho & = & \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \\ \vec{u}_\theta & = & -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \end{array}$ ó $\begin{pmatrix}\vec{u}_\rho \\\vec{u}_\theta\end{pmatrix} = \begin{pmatrix}\cos(\theta) & \mathrm{sen}(\theta)\\ -\mathrm{sen}(\theta) & \cos(\theta)\end{pmatrix}\cdot \begin{pmatrix}\vec{\imath} \\\vec{\jmath}\end{pmatrix}$

y su inverso

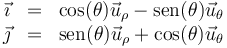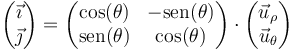
$\begin{array}{rcl} \vec{\imath} & = & \cos(\theta)\vec{u}_\rho-\mathrm{sen}(\theta)\vec{u}_\theta \\ \vec{\jmath} & = & \mathrm{sen}(\theta)\vec{u}_\rho+\cos(\theta)\vec{u}_\theta \end{array}$ ó $\begin{pmatrix}\vec{\imath} \\\vec{\jmath}\end{pmatrix} = \begin{pmatrix}\cos(\theta) & -\mathrm{sen}(\theta)\\ \mathrm{sen}(\theta) & \cos(\theta)\end{pmatrix}\cdot \begin{pmatrix}\vec{u}_\rho \\\vec{u}_\theta\end{pmatrix}$

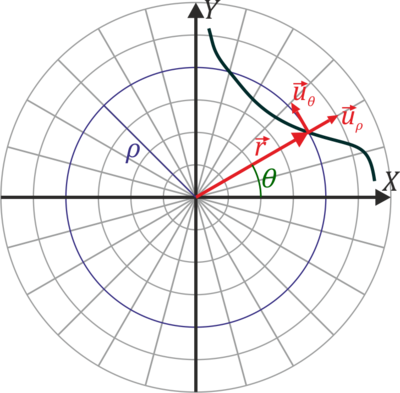
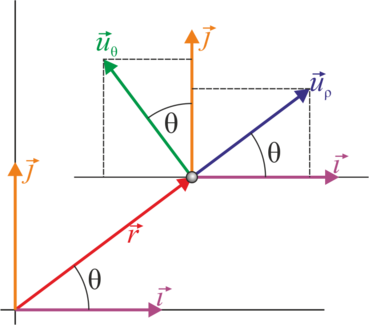
Los vectores unitarios en polares dependen de la posición. Aunque tengan el mismo nombre, el vector 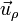$\vec{u}_\rho$ en un punto es diferente del vector 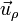$\vec{u}_\rho$ en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares.

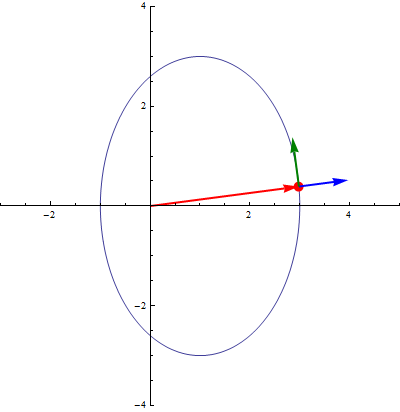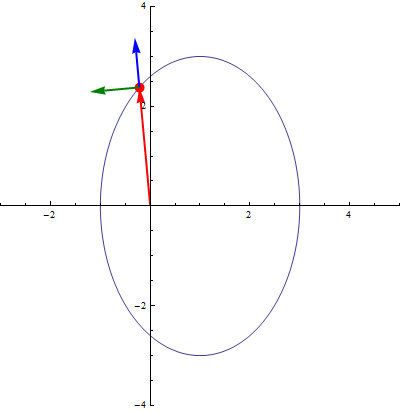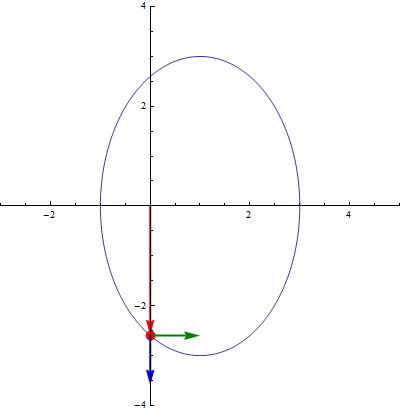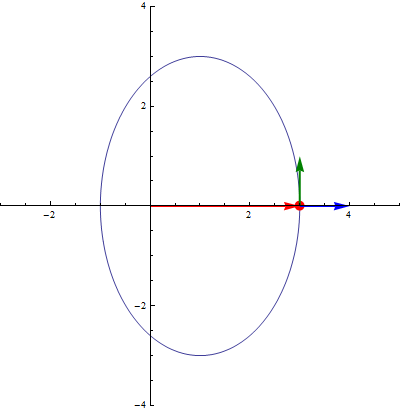
En particular, cuando consideramos el movimiento de una partícula, su posición, y por tanto los vectores de la base en polares, son funciones del tiempo. Por ello, cuando aparezca una derivada o una integral, habrá que tenerlos en cuenta. Sus derivadas respecto del tiempo valen

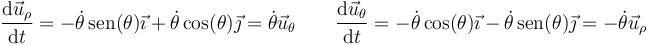
$\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}=-\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}\,+\,\dot{\theta}\cos(\theta)\vec{\jmath}=\dot{\theta}\vec{u}_\theta\qquad \frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}=-\dot{\theta}\cos(\theta)\vec{\imath}\,-\,\dot{\theta}\,\mathrm{sen}(\theta)\vec{\jmath}=-\dot{\theta}\vec{u}_\rho$

2.3.1 Posición en polares

Puesto que el vector 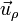$\vec{u}_\rho$ es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es

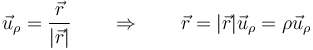
$\vec{u}_\rho = \frac{\vec{r}}{|\vec{r}|} \qquad\Rightarrow\qquad \vec{r}=|\vec{r}|\vec{u}_\rho = \rho\vec{u}_\rho$

2.3.2 Velocidad en polares

la velocidad la calculamos derivando esta expresión respecto al tiempo, donde debemos recordar que también hay que derivar el vector unitario. Aplicamos la derivada de un producto

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}\rho}{\mathrm{d}t}\vec{u}_\rho + \rho\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta$

Esta expresión nos dice que la velocidad se compone de dos partes, una radial, debida a que la partícula se acerca o aleja del origen de coordenadas, y una acimutal, asociada al giro en torno a éste.

Por ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen,

$\rho = A = \mathrm{cte}\qquad\Rightarrow\qquad \dot{\rho}=0\qquad\qquad \dot{\theta}=\omega$

y resulta la velocidad

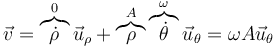
$\vec{v} = \overbrace{\dot{\rho}}^{0}\vec{u}_\rho + \overbrace{\rho}^{A}\overbrace{\dot{\theta}}^{\omega}\vec{u}_\theta = \omega A\vec{u}_\theta$

En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen.

Sin embargo, el que la velocidad acimutal sea distinta de cero (que visto desde el origen se vea girar), no implica que el movimiento sea circular, ni siquiera curvo.

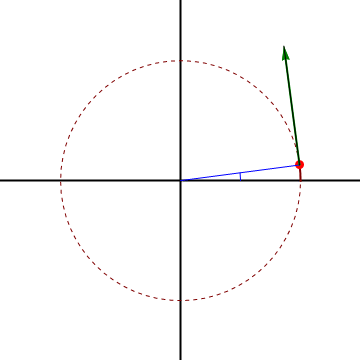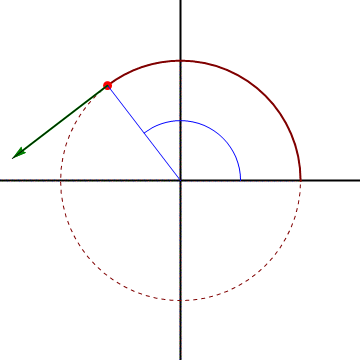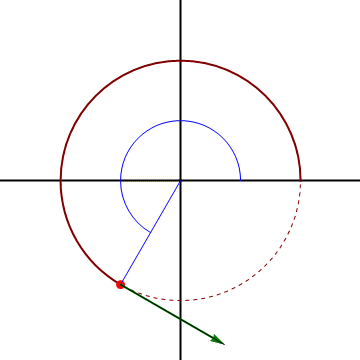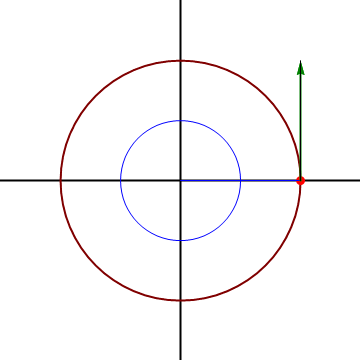
Consideremos el caso de una partícula que sigue un movimiento rectilíneo y uniforme a lo largo de una recta paralela al origen de forma que

$x = L\qquad y = v_0 t$

La expresión de este movimiento en polares es

$\rho = \sqrt{x^2+y^2} = \sqrt{L^2+v_0^2t^2}\qquad\qquad\theta=\,\mathrm{arctg}\left(\frac{y}{x}\right)=\,\mathrm{arctg}\left(\frac{v_0t}{L}\right)$

Las derivadas respecto al tiempo de estas dos magnitudes valen

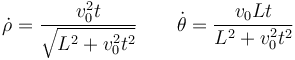
$\dot{\rho}=\frac{v_0^2 t}{\sqrt{L^2+v_0^2 t^2}}\qquad \dot{\theta} = \frac{v_0L t}{L^2+v_0^2t^2}$

y esto nos da la velocidad instantánea

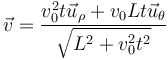
$\vec{v}=\frac{v_0^2 t\vec{u}_\rho+v_0Lt\vec{u}_\theta}{\sqrt{L^2+v_0^2t^2}}$

vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro.

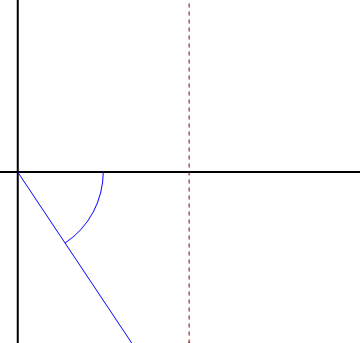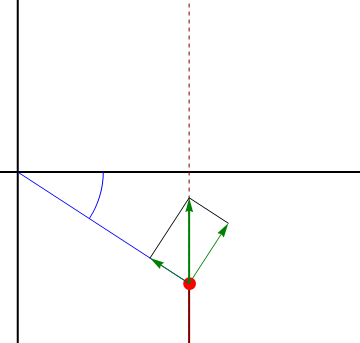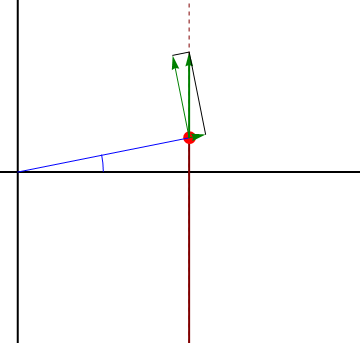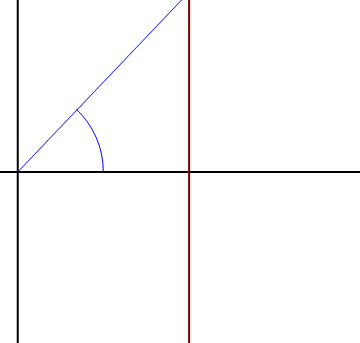
2.3.3 Aceleración en polares

Operando igualmente obtenemos la expresión de la aceleración en polares, solo que esta vez debemos derivar más términos y también el vector 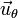$\vec{u}_\theta$

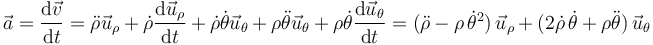
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{\rho}\vec{u}_\rho + \dot{\rho}\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} +\dot{\rho}\dot{\theta}\vec{u}_\theta+\rho\ddot{\theta}\vec{u}_\theta+\rho\dot{\theta}\frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}=(\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta}$

En el caso del movimiento circular tenemos que, para la coordenada radial

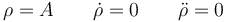
$\rho = A\qquad\dot{\rho}=0\qquad \ddot{\rho}=0$

y para la acimutal

$\dot{\theta}=\omega\qquad\ddot{\theta}=\alpha$

lo que nos da la aceleración lineal

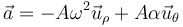
$\vec{a}=-A\omega^2\vec{u}_\rho+A\alpha\vec{u}_\theta$

En general tendrá tanto componente radial (que en este caso coincide con la aceleración normal) como componente acimutal (que en este caso coincide con la tangencial).

En el caso del movimiento rectilíneo y uniforme, tras una serie de cálculos bastante laboriosos se llega a que

$\ddot{\rho}-\rho\,\dot{\theta}^2=0\qquad\qquad \rho\ddot{\theta}+2\dot{\rho}\dot{\theta}=0$

y por tanto

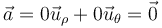
$\vec{a}=0\vec{u}_\rho+0\vec{u}_\theta = \vec{0}$

como corresponde a un movimiento rectilíneo y uniforme.

2.3.4 Resumen de expresiones

Los vectores de posición, velocidad y aceleración en este sistema quedan, por tanto,

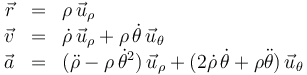
$\begin{array}{rcl} \vec{r} & = & \rho\,\vec{u}_{\rho}\\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta}\\ \vec{a} & = &(\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta} \end{array}$

En coordenadas polares, la rapidez es igual a

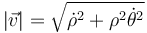
$|\vec{v}| = \sqrt{\dot{\rho}^2+\rho^2\dot{\theta}^2}$

Como ejemplo de movimiento que es más fácil de expresar en coordenadas polares que en cartesianas, consideremos una partícula que describe una espiral de Arquímedes, en la cual la distancia al centro aumenta linealmente con el tiempo. Empleando coordenadas cartesianas, la ecuación horaria es

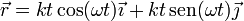
$\vec{r} = k t\cos(\omega t)\vec{\imath}+k t\,\mathrm{sen}(\omega t)\vec{\jmath}$

lo cual, a la hora de derivar para hallar la velocidad y la aceleración puede ser bastante engorroso. En coordenadas polares se expresa

$\rho = k t\qquad\qquad\theta = \omega t$

y la velocidad y aceleración son inmediatas

$\vec{v} = k\vec{u}_\rho + k\omega t\vec{u}_\theta\qquad \vec{a}=-k\omega^2t \vec{u}_\rho+ 2k\omega \vec{u}_\theta$

2.4 Coordenadas cilíndricas

Las coordenadas polares pueden extenderse a tres dimensiones añadiendo una tercera coordenada cartesiana, que sería la altura $z$ .

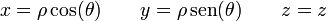
$x = \rho\cos(\theta) \qquad y = \rho\,\mathrm{sen}(\theta)\qquad z = z$

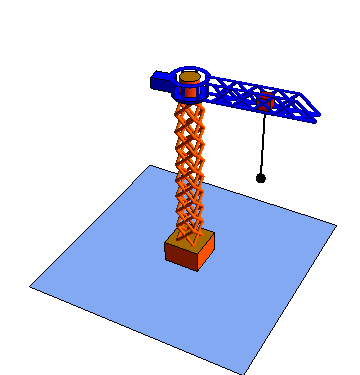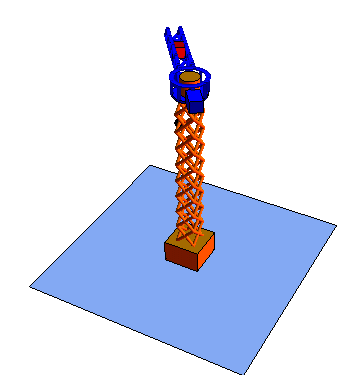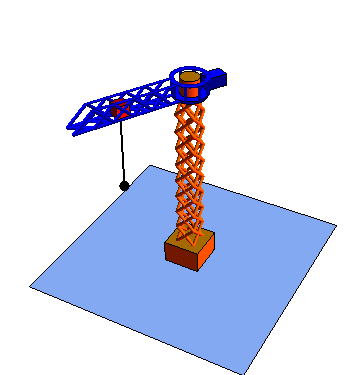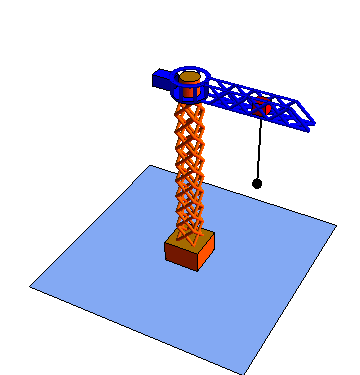
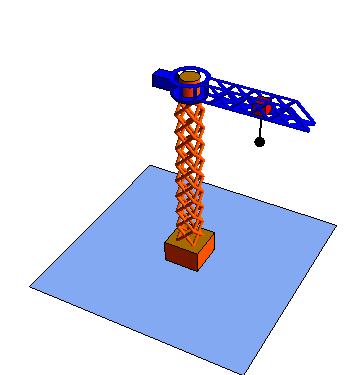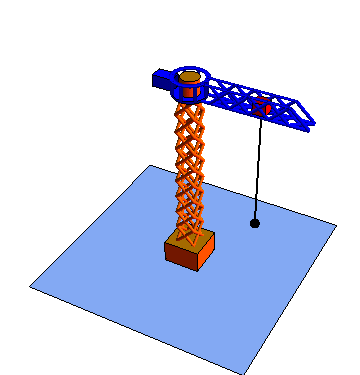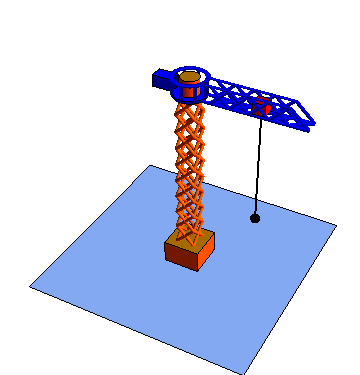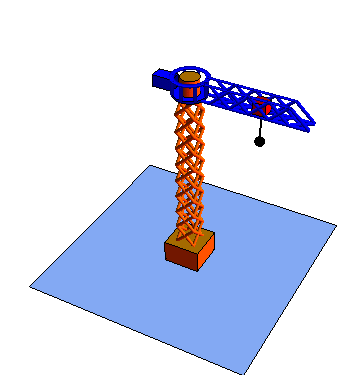
Estas tres coordenadas se denomina respectivamente radial, acimutal y vertical

Movimiento radial	Movimiento acimutal	Movimiento vertical

La base vectorial se amplía simplemente añadiendo el vector $\vec{k}$

$\begin{array}{rcl} \vec{u}_\rho & = & \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \\ \vec{u}_\theta & = & -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \\ \vec{k} & = & \vec{k} \end{array}$

Esta base es ortonormal y dextrógira.

En coordenadas cilíndricas la posición, velocidad y aceleración quedan

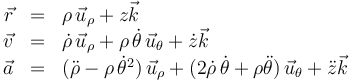
$\begin{array}{rcl} \vec{r} & = & \rho\,\vec{u}_{\rho}+z\vec{k}\\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta}+\dot{z}\vec{k}\\ \vec{a} & = &(\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta}+\ddot{z}\vec{k} \end{array}$

Un movimiento sencillo de representar en coordenadas cilíndricas sería el de una hélice (no confundir con una espiral), recorrida con rapidez constante

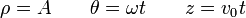
$\rho = A\qquad\theta = \omega t \qquad z = v_0t\,$

3 Ejemplos de movimientos

3.1 Parabólico

El movimiento parabólico, característico del tiro de un proyectil, se caracteriza por tener una aceleración constante debida a la gravedad

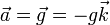
$\vec{a}=\vec{g}=-g\vec{k}$

(tomando como eje Z el perpendicular al suelo y dirigido hacia arriba). Integrando esta ecuación una vez obtenemos la velocidad instantánea

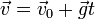
$\vec{v} = \vec{v}_0 + \vec{g}t$

y una nueva integración nos da la posición instantánea:

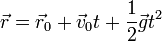
$\vec{r}=\vec{r}_0 + \vec{v}_0t+\frac{1}{2}\vec{g}t^2$

Este movimiento es plano, ya que su aceleración es constante y por tanto

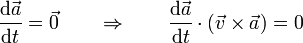
$\frac{\mathrm{d}\vec{a}}{\mathrm{d}t}=\vec{0}\qquad\Rightarrow\qquad \frac{\mathrm{d}\vec{a}}{\mathrm{d}t}\cdot(\vec{v}\times\vec{a})=0$

Si tomamos el eje X como el que pertenece al plano de movimiento podemos escribir la posición instantánea como

$\vec{r}=(x_0+v_{x0}t)\vec{\imath}+\left(z_0+v_{z0}t-\frac{1}{2}gt^2\right)\vec{k}$

Esta ecuación puede leerse como que el movimiento parabólico es una superposición de un movimiento uniforme en la dirección horizontal y uno uniformemente acelerado en la dirección vertical.

Eliminando el tiempo entre las dos coordenadas obtenemos una ecuación para la trayectoria

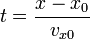
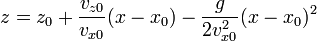
$t = \frac{x-x_0}{v_{x0}}$ $\Rightarrow$ $z = z_0 + \frac{v_{z0}}{v_{x0}}(x-x_0) -\frac{g}{2v_{x0}^2}(x-x_0)^2$

Al tratarse de un polinomio de segundo grado, es claro que la trayectoria es una parábola dirigida hacia abajo.

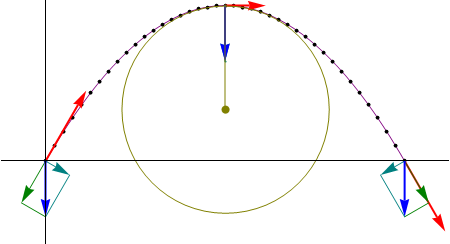
Aunque la aceleración sea constante, tanto la aceleración tangencial como la normal son funciones del tiempo. La celeridad de la partícula disminuye al ascender y vuelve a aumentar al descender, alcanzando su mínimo en el vértice de la parábola. En este punto, la aceleración tangencial es nula y toda la aceleración es puramente normal.

3.2 Circular

Un movimiento circular merece un estudio pormenorizado por su amplio uso. Consideraremos primero el caso del movimiento circular en el plano OXY, que permite un tratamiento simplificado y posteriormente generalizaremos a tres dimensiones.

3.2.1 En el plano OXY

Puesto que los sistemas de referencia son arbitrarios, una vez que sabemos que un movimiento es circular, podemos tomar el origen de coordenadas en el centro de la circunferencia y los ejes de forma que la trayectoria esté contenida en el plano XY y con el origen de coordenadas en el centro de la circunferencia. En coordenadas polares, una circunferencia centrada en el origen se escribe simplemente

$\rho = R\,$

La ecuación vectorial de la trayectoria se reduce a

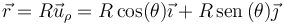
$\vec{r}=R\vec{u}_\rho = R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}\,(\theta)\vec{\jmath}$

siendo la ley horaria

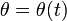
$\theta = \theta(t)\,$

La velocidad de un movimiento circular es puramente acimutal,

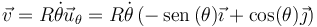
$\vec{v}=R\dot{\theta}\vec{u}_\theta = R\dot{\theta}\left(-\,\mathrm{sen}\,(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right)$

siendo la rapidez y el vector tangente

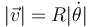
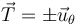
$|\vec{v}| = R|\dot{\theta}|$ $\vec{T}=\pm \vec{u}_\theta$

El signo variable depende del sentido de recorrido sobre la circunferencia. Por ejemplo, el movimiento de la lenteja de un péndulo es circular (aunque no complete una circunferencia) pero en su vaivén, el vector tangente unas veces coincide con el unitario en la dirección acimutal y otras es el opuesto.

La distancia medida sobre la curva

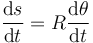
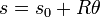
$\frac{\mathrm{d}s}{\mathrm{d}t}= R\frac{\mathrm{d}\theta}{\mathrm{d}t}$ $\Rightarrow$ $s = s_0+R\theta\,$

A la derivada respecto al tiempo del ángulo de giro se la denomina velocidad angular (escalar)

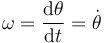
$\omega = \frac{\mathrm{d}\theta}{\mathrm{d}t}=\dot{\theta}$

de forma que la rapidez de la partícula se puede escribir como

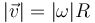
$|\vec{v}|=|\omega|R$

A la derivada respecto al tiempo de la velocidad se la denomina la aceleración angular

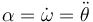
$\alpha = \dot{\omega}=\ddot{\theta}$

Para la aceleración de la partícula, $\vec{a}$ que en este contexto se la llama aceleración lineal, para distinguirla de la angular tenemos, en coordenadas polares

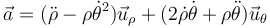
$\vec{a}=(\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho + (2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{u}_\theta$

Si sustituimos los valores ya conocidos queda

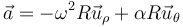
$\vec{a}=-\omega^2R\vec{u}_\rho + \alpha R\vec{u}_\theta$

Esta aceleración se compone de dos términos. El proimero es ortogonal a la velocidad y el segundo es paralelo a ella, por lo que la aceleración tangencial es

$\vec{a}_t=\alpha R\vec{u}_\theta \qquad\qquad a_t=\alpha R$

y la normal

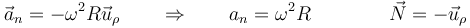
$\vec{a}_n=-\omega^2R\vec{u}_\rho\qquad\Rightarrow\qquad a_n=\omega^2R\qquad\qquad \vec{N}=-\vec{u}_\rho$

Vemos que la aceleración normal apunta radialmente hacia el interior de la circunferencia y que su módulo va como el cuadrado de la velocidad angular, cumpliéndose,

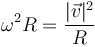
$\omega^2R=\frac{|\vec{v}|^2}{R}$

3.2.2 Expresión vectorial

Los resultados anteriores pueden expresarse en forma vectorial definiendo el vector velocidad angular

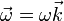
$\vec{\omega}=\omega\vec{k}$

siendo $\vec{k}$ el vector unitario en la dirección ortogonal al plano. Este vector coincide con el vector binormal asociado al movimiento.

Análogamente se define el vector aceleración angular

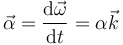
$\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}=\alpha\vec{k}$

Estos dos vectores son paralelos al eje de giro y suelen aplicarse en el centro de la circunferencia. los dos tienen la misma dirección. El sentido es coincidente si la aceleración tangencial es positiva y opuesto si es negativa.

Con ayuda del vector velocidad angular, la velocidad lineal puede escribirse como

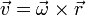
$\vec{v}=\vec{\omega}\times\vec{r}$

y la aceleración lineal

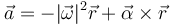
$\vec{a}=-|\vec{\omega}|^2\vec{r}+\vec{\alpha}\times\vec{r}$

A su vez, por las propiedades del doble producto vectorial esto es igual a_n

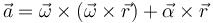
$\vec{a}=\vec{\omega}\times(\vec{\omega}\times\vec{r})+\vec{\alpha}\times\vec{r}$

siendo las componentes intrínsecas de la aceleración

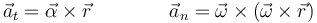
$\vec{a}_t=\vec{\alpha}\times\vec{r}\qquad\qquad \vec{a}_n=\vec{\omega}\times(\vec{\omega}\times\vec{r})$

Lo anterior está expresado suponiendo que el centro de la circunferencia es el origen de coordenadas. La velocidad puede escribirse también en la forma

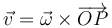
$\vec{v}=\vec{\omega}\times\overrightarrow{OP}$

Si el centro del movimiento circular no se halla en el origen sino en otro punto C, la generalización es inmediata

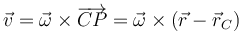
$\vec{v}=\vec{\omega}\times\overrightarrow{CP}=\vec{\omega}\times(\vec{r}-\vec{r}_C)$

3.2.3 Caso general

En el caso general el plano de movimiento puede tener cualquier orientación respecto a los ejes y su centro puede ser cualquier punto del espacio. Para caracterizar un movimiento como circular debemos verificar que

El movimiento es plano: Existe un vector constante $\vec{B}$ tal que

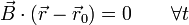
$\vec{B}\cdot(\vec{r}-\vec{r}_0)=0\qquad\forall t$

El radio de curvatura permanece constante:

$R = \frac{|\vec{v}|^2}{a_n}=\mathrm{cte}\qquad\forall t$

Estas dos condiciones pueden reducirse a una sola:

El centro de curvatura permanece constante:

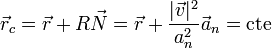
$\vec{r}_c = \vec{r}+R\vec{N}=\vec{r}+\frac{|\vec{v}|^2}{a_n^2}\vec{a}_n=\mathrm{cte}$

Por tanto, dadas la ecuación horaria del movimiento o, más en general, la trayectoria en función de cualquier parámetro, si calculamos el centro de curvatura y resulta un vector constante el movimiento es circular, aunque en la expresión no sea evidente.

3.2.4 Velocidad angular

En cualquier movimiento, se verifica en todo instante que

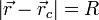
$\left|\vec{r}-\vec{r}_c\right| = R$

en el caso particular de un movimiento circular $R$ y $\vec{r}_c$ son constantes, por lo que si elevamos al cuadrado esta expresión

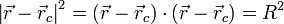
$\left|\vec{r}-\vec{r}_c\right|^2 = (\vec{r}-\vec{r}_c)\cdot(\vec{r}-\vec{r}_c)=R^2$

y derivamos respecto al tiempo

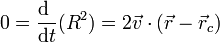
$0 = \frac{\mathrm{d}\ }{\mathrm{d}t}(R^2) = 2\vec{v}\cdot(\vec{r}-\vec{r}_c)$

esto es, la velocidad es siempre perpendicular al vector de posición relativa al centro de la circunferencia. Esta ortogonalidad permite escribir la velocidad como

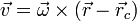
$\vec{v} = \vec{\omega}\times\left(\vec{r}-\vec{r}_c\right)$

donde $\vec{\omega}$ es la velocidad angular. Es un vector perpendicular al plano de la trayectoria circular y con un sentido tal que se verifica la regla de la mano derecha respecto al giro (si los dedos de la mano derecha apuntan en la dirección del giro, el pulgar marca la dirección y sentido de la velocidad angular).

La velocidad angular posee dimensiones de 1/tiempo, con lo que en el sistema internacional se mide en s^-1 o rad/s.

3.2.5 Aceleración angular

Derivando en la expresión anterior para la velocidad

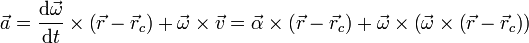
$\vec{a}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}\times\left(\vec{r}-\vec{r}_c\right)+\vec{\omega}\times\vec{v}=\vec{\alpha}\times\left(\vec{r}-\vec{r}_c\right)+\vec{\omega}\times\left(\vec{\omega}\times\left(\vec{r}-\vec{r}_c\right)\right)$

El vector

$\vec{\alpha} = \frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}$

es la aceleración angular del movimiento. En el sistema internacional, sus unidades son rad/s².

3.2.6 Movimiento circular uniforme

El movimiento circular uniforme es el que ocurre a celeridad constante

$v = v_0=\mathrm{cte}\qquad \Leftrightarrow \qquad \vec{a}_t=\vec{0}$

En este movimiento la velocidad no es constante, puesto que su dirección está cambiado. La aceleración es puramente normal

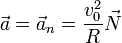
$\vec{a}=\vec{a}_n = \frac{v_0^2}{R}\vec{N}$

lo que implica que la aceleración va en la dirección de la posición relativa al centro de la circunferencia, y dirigida hacia adentro y puesto que estos dos vectores son de módulo constante se cumple

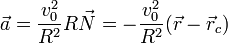
$\vec{a} = \frac{v_0^2}{R^2}R\vec{N}=-\frac{v_0^2}{R^2}(\vec{r}-\vec{r}_c)$

En un movimiento circular uniforme la velocidad angular es constante

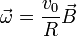
$\vec{\omega}=\frac{v_0}{R}\vec{B}$

siendo $\vec{B}$ el vector normal al plano de la circunferencia. La aceleración angular es nula

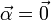
$\vec{\alpha}=\vec{0}$

La aceleración puede escribirse en términos de la velocidad angular como

$\vec{a}=\vec{\omega}\times(\vec{\omega}\times(\vec{r}-\vec{r}_c))=-\omega^2(\vec{r}-\vec{r}_c)$

Un movimiento circular uniforme es periódico, siendo el periodo de revolución el tiempo necesario para dar una vuelta completa

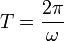
$T = \frac{2\pi}{\omega}$

Al número de vueltas que la partícula da por segundo se le denomina la frecuencia natural

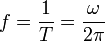
$f = \frac{1}{T}=\frac{\omega}{2\pi}$

3.3 Oscilador armónico

El movimiento armónico simple se define como el que es:

Rectilíneo
Cumple la ecuación de movimiento

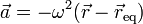
$\vec{a}=-\omega^2(\vec{r}-\vec{r}_\mathrm{eq})$

Por ejemplo, el movimiento, descrito en un problema

$\vec{r}(t)=A\cos^2(\omega t)\vec{\imath}+2A\,\mathrm{sen}^2(\omega t)\vec{\jmath}+2A\cos^2(\omega t)\vec{k}$

es armónico simple, sin embargo el movimiento

$\vec{r} = A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}(\omega t)\vec{\jmath}$

no lo es, por no ser rectilíneo (es circular uniforme).

No obstante, lo anterior, el comportamiento de un oscilador armónico puede generalizarse a tres dimensiones como aquel movimiento que verifica la ecuación

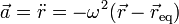
$\vec{a}=\ddot{r}=-\omega^2(\vec{r}-\vec{r}_\mathrm{eq})$

Si medimos la posición respecto al punto de equilibrio, sustituyendo 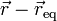$\vec{r}-\vec{r}_\mathrm{eq}$ por $\vec{r}$ (entendiendo que tomamos como origen el punto de equilibrio), esta ecuación se reduce a

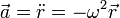
$\vec{a}=\ddot{r}=-\omega^2\vec{r}$

La solución general de esta ecuación diferencial es de la forma

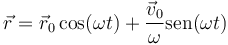
$\vec{r}=\vec{r}_0\cos(\omega t) + \frac{\vec{v}_0}{\omega}\mathrm{sen}(\omega t)$

siendo 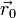$\vec{r}_0$ y $\vec{v}_0$ la posición y la velocidad iniciales.

Como en el caso unidimensional, este movimiento es periódico, con periodo

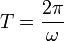
$T = \frac{2\pi}{\omega}$

Sin embargo, en general no se trata de un movimiento rectilíneo, sino elíptico alrededor del punto de equilibrio. Solo será rectilíneo si la posición y la velocidad inicial son vectores paralelos o alguno de ellos es nulo.

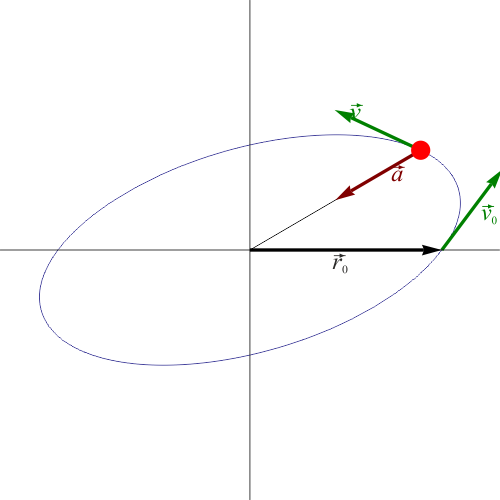
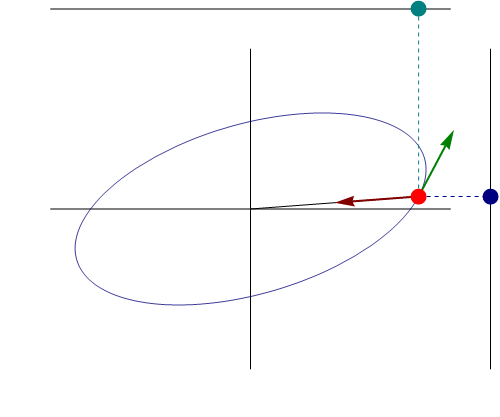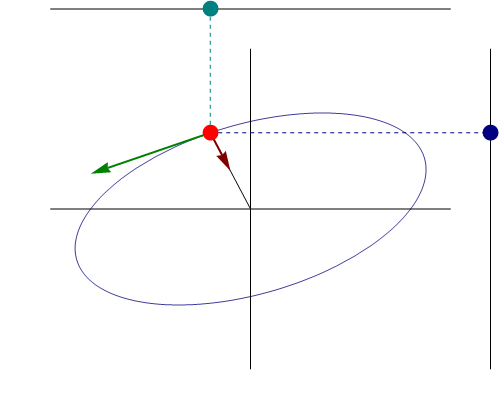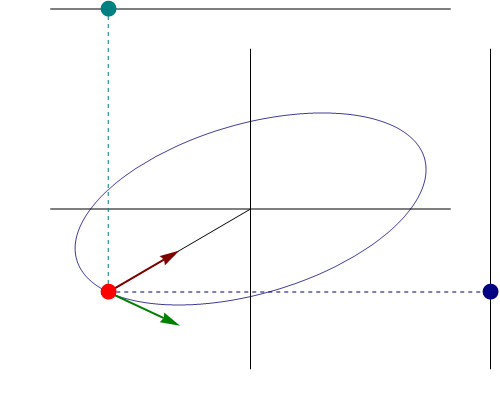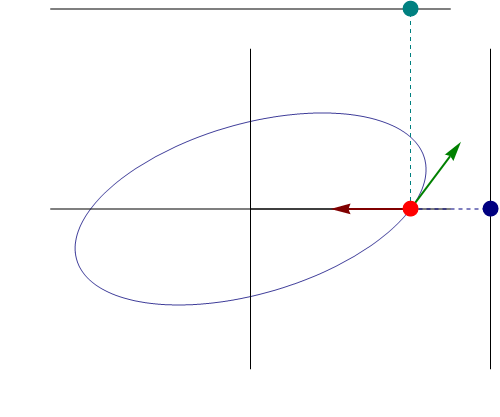
Si separamos en sus componentes cartesianas, el movimiento tridimensional equivale a la superposición de tres movimientos armónicos unidimensionales

$\begin{array}{rcl}x & = & \displaystyle x_0\cos(\omega t) + \frac{v_{x0}}{\omega}\mathrm{sen}(\omega t) \\ & & \\ y & = & \displaystyle y_0\cos(\omega t) + \frac{v_{y0}}{\omega}\mathrm{sen}(\omega t) \\ & & \\ z & = & \displaystyle z_0\cos(\omega t) + \frac{v_{z0}}{\omega}\mathrm{sen}(\omega t)\end{array}$