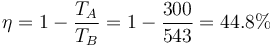Caso práctico de ciclo Brayton (GIE)
De Laplace
Contenido |
1 Enunciado
Un ciclo Brayton (o Joule) ideal modela el comportamiento de una turbina, como las empleadas en las centrales térmicas de gas natural. Este ciclo está formado por cuatro pasos que aproximamos como cuasiestáticos, según se indica en la figura.
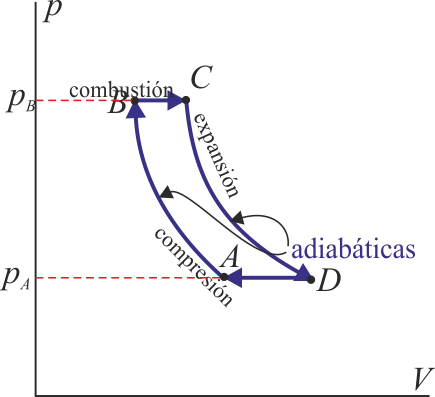
Suponga que el estado inicial corresponde a un volumen de 1L de aire seco a p_A=100 kPa y T_A=300 K. El ciclo descrito por este gas es el siguiente: A→B: Se comprime adiabáticamente hasta una presión p_B=800 kPa. B→C: Se calienta el gas mediante una combustión a presión constante, siendo el poder calorífico del combustible 800kJ por cada kg de aire. C→D: Se expande de forma adiabática hasta que la presión vuelve a ser la inicial. D→A: Se comprime el gas a presión constante hasta que retorna al estado inicial. Para este proceso:
- Determine la presión, volumen y temperatura en cada uno de los estados B, C y D.
- Calcule el calor que entra y el que sale en el sistema, así como el trabajo neto realizado por el gas sobre el ambiente a lo largo de un ciclo.
- A partir del calor y el trabajo halle el rendimiento del ciclo.
- Este mismo rendimiento puede hallarse a partir de las temperaturas de los estados A y B. Obtenga la expresión general para el rendimiento en función de estas dos temperaturas y calcúlelo para este ciclo concreto.
Datos: Constante universal de los gases ideales: R=8.314 J\/K·mol; cociente de capacidades caloríficas para el aire: γ=1.4; peso molecular medio del aire: P_m=28.96 g\/mol.
2 Estados B, C y D
| p (kPa) | V (L) | T (K) | |
|---|---|---|---|
| A | 100 | 1.000 | 300 |
| B | 800 | 0.226 | 543 |
| C | 800 | 0.558 | 1340 |
| D | 100 | 2.465 | 740 |
En todos los procesos se cumple la ley de los gases ideales
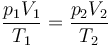
Además en los adiabáticos se cumple la ley de Poisson
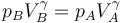
Para hallar la temperatura del estado C se halla previamente la masa de gas
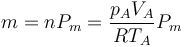
y el calor de entrada
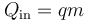
La temperatura sale de que es un proceso a presión constante
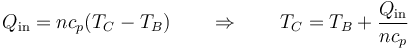
con cp = 3.5R
3 Calor y trabajo
3.1 Calor de entrada
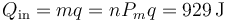
3.2 Calor de salida
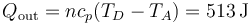
3.3 Trabajo neto
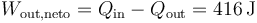
4 Rendimiento
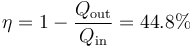
5 Rendimiento en función de las temperaturas
Tal como se ve en un problema resuelto