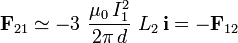Campo magnético de dos corrientes filiformes rectilíneas (F2GIA)

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Campo magnético de dos corrientes rectilíneas paralelas 2.2 Campo nulo en puntos del plano de las corrientes 2.3 Interacción entre las corrientes

1 Enunciado

Dos hilos conductores rectilíneos Δ₁ y Δ₂, de longitud indefinida, se disponen en paralelo separados una distancia d. Cuando son recorridos por sendas corrientes eléctricas estacionarias I₁ e I₂, medidas en los sentidos indicados en la figura, se observa que el campo magnético se anula en un punto situado a una distancia d / 2 de Δ₁ y 3d / 2 de Δ₂, y que se halla contenido en el mismo plano que los hilos conductores.

1. Si la intensidad de la corriente I₁ es de 1 A, ¿cuál es la intensidad de la corriente I₂?
2. ¿Cómo es la interacción entre los hilos?

2 Solución

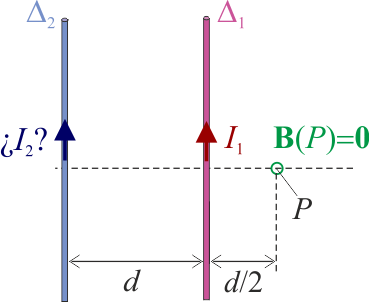
Para obtener una solución detallada y completa del ejercicio propuesto comenzaremos por analizar el problema general del campo magnético creado por dos corrientes eléctricas que recorren sendos conductores rectilíneos y paralelos que pueden considerarse como filiformes; es decir, su sección es despreciable frente a otras dimensiones del sistema, como pueden ser las longitudes de los conductores y la distancia que los separa. Para ello, adoptaremos un sistema de coordenadas en el cuál el eje OZ coincida con el hilo conductor Δ₁, y que ambos hilos estén contenidos en el plano OXZ, en el cual, el valor de la coordenada y es nulo para todos sus puntos.

2.1 Campo magnético de dos corrientes rectilíneas paralelas

El campo magnético creado por este sistema de corrientes puede obtenerse como la superposición de los campos que crearían cada una de ellas por separado. Obsérvese que la expresión para el campo magnético , creado por la corriente de intensidad I₁ que recorre el hilo Δ₁, debe ser idéntica a la obtenida en aquel ejercicio, al hacer coincidir el hilo con el eje OZ. Por tanto, el valor de dicho campo magnético en un punto de coordenadas arbitrarias P(x,y,z), cuya posición viene dada por el radio-vector , medido desde un punto fijo O del hilo Δ₁, será:

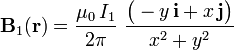
Las líneas de campo son circunferencias con centro en el eje Δ₁ y contenidas en planos perpendiculares a dicho eje. Y al considerar el elemento de corriente en el sentido del unitario 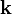, este campo magnético “circulará” en sentido antihorario para valores positivos de la intensidad I₁, y en sentido horario si dicha intensidad es negativa.

El campo creado por la corriente I₂ en el conductor filiforme Δ₂ debe ser análogo al anterior si utilizamos un sistema de referencia cartesiano, obtenido al trasladar el eje OZ una distancia d en el sentido negativo del eje OX. Con esta transformación de ejes, las coordenadas de un punto arbitrario serían 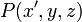, siendo . En consecuencia, la expresión del campo magnético creado por la corriente que recorre Δ₂, será:

Nuevamente, las líneas de este campo son circunferencias contenidas en planos perpendiculares a Δ₂ y concéntricas con dicho eje, circulando en sentido antihorario u horario, en función de que el valor de la intensidad I₂ se positivo o negativo.

Aplicando el principio se superposición, se tendrá que el campo magnético total es la resultante en cada punto de los campos creados por cada una de las corrientes rectilíneas:

cuyas líneas de campo serán curvas no abiertas contenidas en planos perpendiculares a los hilos, pero que no van a ser circunferencias.

2.2 Campo nulo en puntos del plano de las corrientes

En el sistema de referencia adoptado, los conductores filiformes están contenidos en el plano OXZ, cuyos puntos vendrán dados por ternas de coordenadas P(x,0,z). Por tanto, el campo magnético total en un punto arbitrario de dicho plano será de la forma,

Sea P₀ un punto de dicho plano donde se anula el campo magnético total. Si, según el enunciado, este punto se encuentra a sendas distancias d / 2 y 3d / 2 de los conductores Δ₁ y Δ₂, el valor de su coordenada x en el sistema de referencia será x₀ = d / 2. En consecuencia, la condición para que el campo se anule en dicho punto es,

Es decir, considerando que los elementos de corriente en los dos hilos tienen la dirección y el sentido del vector unitario 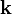, se llega a la conclusión de que para que se verifique la situación descrita en el enunciado, es necesario que las intensidades de corriente tengan distinto signo; o lo que es lo mismos, deben recorrer los hilos en sentidos opuestos. En concreto, si el conductor Δ₁ es recorrido por una corriente eléctrica de 1 A, en el sentido positivo del unitario 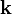, en el conductor Δ₂ debe haber una corriente de -3 A, medida en ese sentido. Es decir, la corriente eléctrica recorre el segundo conductor en el sentido indicado por el vector 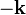, con una intensidad de 3 A.

Esto se traduce en que los campos magnéticos creados por cada una de esta corrientes recorren sus líneas de campo en sentidos opuestos, pudiendo llegar a anularse en deteriminados puntos del plano OXZ.

2.3 Interacción entre las corrientes

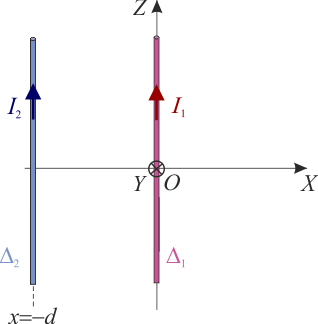
Consideremos un elemento de corriente 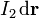en el conductor Δ₂. Dicho elemento va a estar situado en un punto arbitrario de coordenadas P₂( − d,0,z); por tanto, la fuerza elemental ejercida sobre él por el campo magnético creado por la corriente I₁ en Δ₁, será:

Obsérvese que esta fuerza elemental tiene idéntico valor en todos los puntos del conductor Δ₂. Por tanto, la acción de la corriente I₁ sobre la I₂ puede describirse en términos de una fuerza por unidad de longitud, que tiene un valor constante. De esta forma, si consideramos una longitud L₂ del conductor Δ₂, sobre la que actúa el mismo campo magnético , y si se desprecian los efectos de los extremos de los conductores, se tendrá una la fuerza total de interacción será:

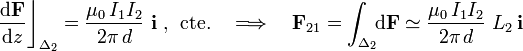
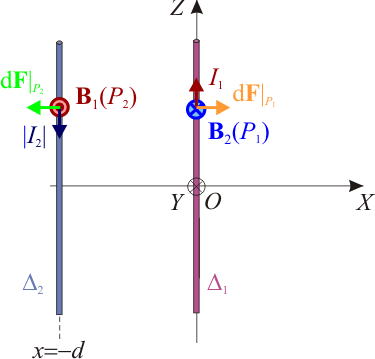
En el caso de que se verifiquen las condiciones del apartado anterior, se obtiene que la corriente de intensidad en Δ₂, y la I₁ en Δ₁, son mútuamente repulsivas: