Entrar Página Discusión Historial Go to the site toolbox

Anillo rotando en el campo de otro anillo

De Laplace

Contenido

1 Enunciado

Se tienen dos anillos metálicos. Ambos anillos están centrados en el origen de coordenadas. Uno de ellos posee radio b y está situado en el plano XY. El otro, de radio a, está inclinado, de forma que su normal forma un ángulo θ con el eje Z. El radio b, es mucho mayor que a.

  1. Determine el coeficiente de inducción mutua entre los dos anillos a partir del flujo del campo del anillo exterior a través del anillo interior (tenga en cuenta que éste es muy pequeño) cuando por el anillo exterior circula una corriente I1.
  2. Suponga que por el anillo exterior se hace circular una corriente constante I0. El anillo interior se hace girar en torno al diámetro común, de forma que el ángulo θ varía con velocidad constante ω.
    1. Despreciando los efectos de la autoinducción, halle la corriente que circula por el anillo interior.
    2. Calcule la energía disipada en este anillo durante un periodo de revolución. ¿De dónde procede esta energía?

2 Coeficiente de inducción mutua

Al ser el anillo interior muy pequeño, podemos suponer que el campo en todos sus puntos debido a la espira exterior es aproximadamente igual al campo en el centro de ésta.

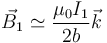
\vec{B}_1\simeq\frac{\mu_0I_1}{2b}\vec{k}

Entonces, al calcular el flujo a través del anillo exterior, podemos suponer que el campo es constante y extraerlo de la integral

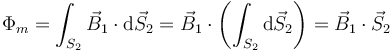
\Phi_m=\int_{S_2}\vec{B}_1\cdot\mathrm{d}\vec{S}_2=\vec{B}_1\cdot\left(\int_{S_2}\mathrm{d}\vec{S}_2\right)=\vec{B}_1\cdot\vec{S}_2

siendo el vector superficie uno que tiene por módulo el área de la superficie apoyada en la espira , por dirección la normal a ella y por sentido el dado por la regla de la mano derecha

\vec{S}_2=\pi a^2\vec{n}

Por tanto, el flujo a través de la espira pequeña es

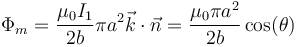
\Phi_m=\frac{\mu_0I_1}{2b}\pi a^2 \vec{k}\cdot\vec{n}=\frac{\mu_0\pi a^2}{2b}\cos(\theta)

con θ el ángulo que forman los dos vectores unitarios. Despejando de aquí obtenemos el coeficiente de inducción mutua

\Phi_m=MI_1 \qquad\Rightarrow\qquad M=\frac{\mu_0\pi a^2}{2b}\cos(\theta)

3 Corriente inducida

Cuando la espira está girando, el ángulo θ va cambiando como

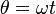
\theta=\omega t\,

por lo que el flujo magnético es una función sinusoidal

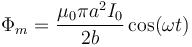
\Phi_m=\frac{\mu_0\pi a^2I_0}{2b}\cos(\omega t)

Por ello, como en el problema de la espira rotatoria, el resultado para la corriente inducida es una corriente alterna

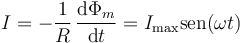
I =-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}=I_\mathrm{max}\mathrm{sen}(\omega t)

con la amplitud

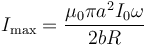
I_\mathrm{max}= \frac{\mu_0\pi a^2I_0\omega}{2bR}

4 Energía disipada

De nuevo como en el problema de la espira rotatoria, en el anillo interior se disipa una potencia

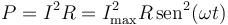
P =I^2R = I_\mathrm{max}^2R\,\mathrm{sen}^2(\omega t)

siendo la energía total disipada en un periodo

W_d = \int_0^T P\,\mathrm{d}t=\frac{I_\mathrm{max}^2RT}{2}
Obtenido de "http://tesla.us.es/wiki/index.php/Anillo_rotando_en_el_campo_de_otro_anillo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 17:20, 10 jun 2015. - Esta página ha sido visitada 2.205 veces. - Aviso legal - Acerca de Laplace