Espira cuadrada que gira en un campo magnético
De Laplace
Contenido |
1 Enunciado
Una espira cuadrada de lado 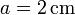 , de hilo de cobre de sección
, de hilo de cobre de sección 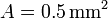 gira con frecuencia
gira con frecuencia 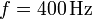 en el interior de un campo magnético uniforme de módulo
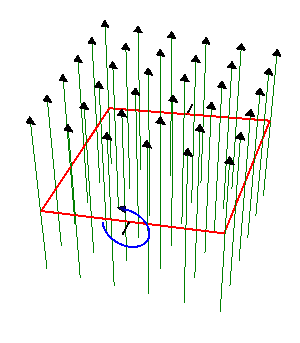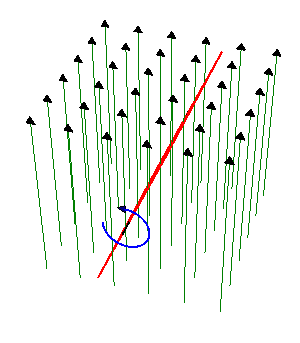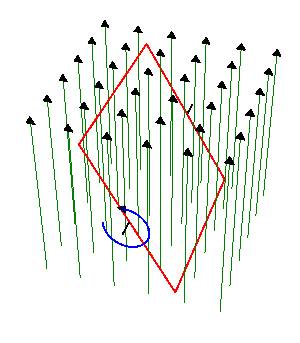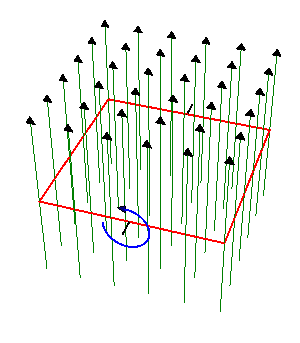
en el interior de un campo magnético uniforme de módulo 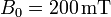 . El eje de giro es perpendicular al campo magnético.
. El eje de giro es perpendicular al campo magnético.
- Determine la corriente que se induce en la espira.
- Calcule la potencia instantánea disipada en la espira y la energía total disipada en un periodo de giro.
2 Cálculo de la intensidad
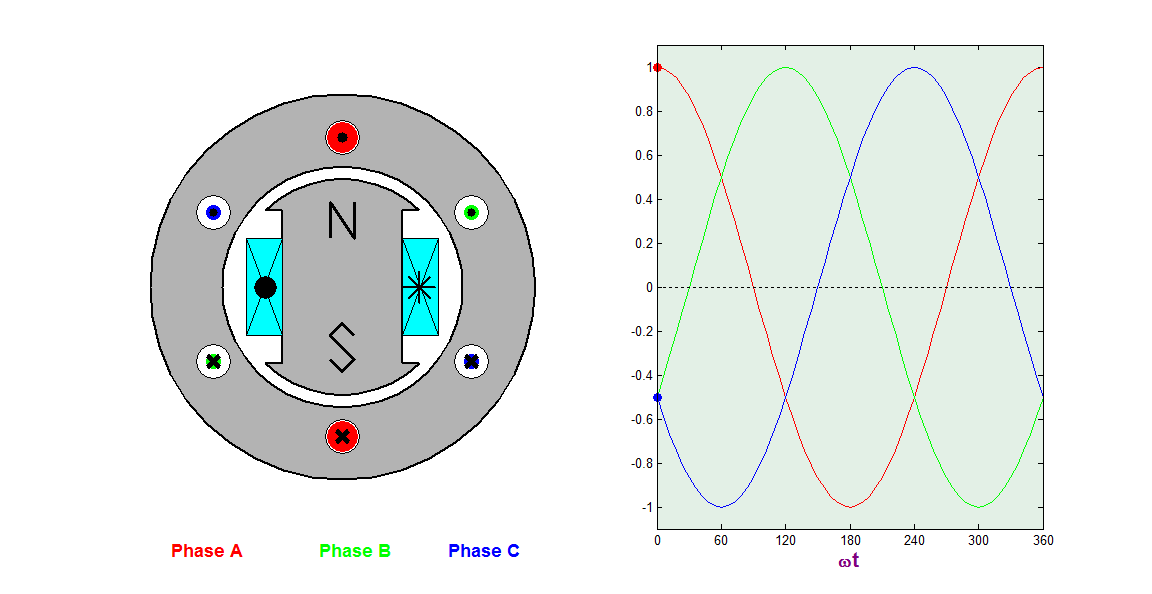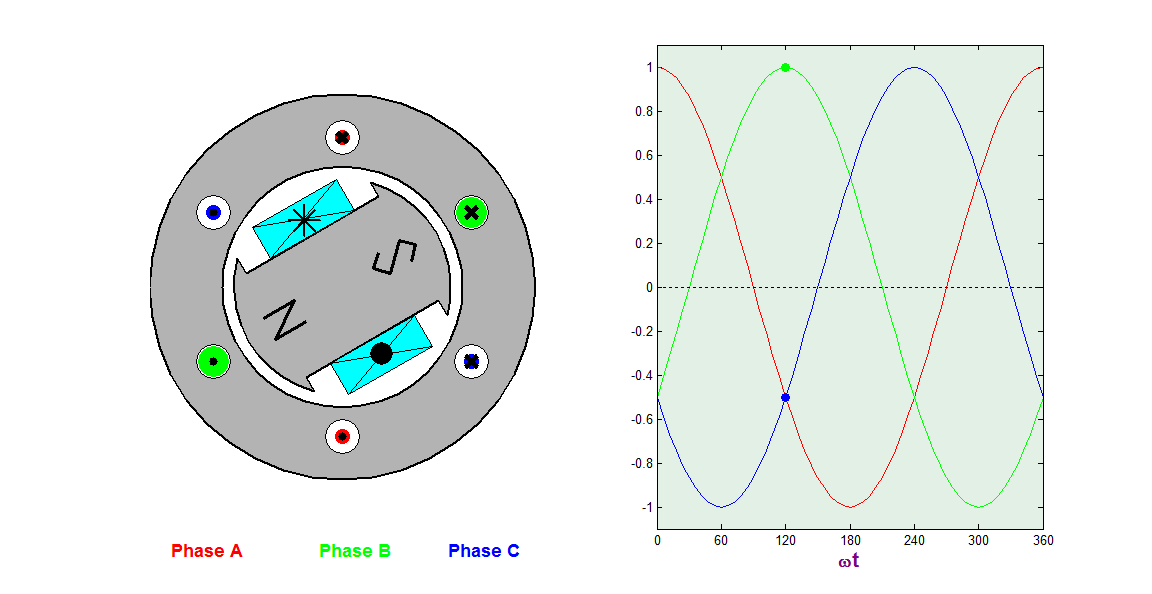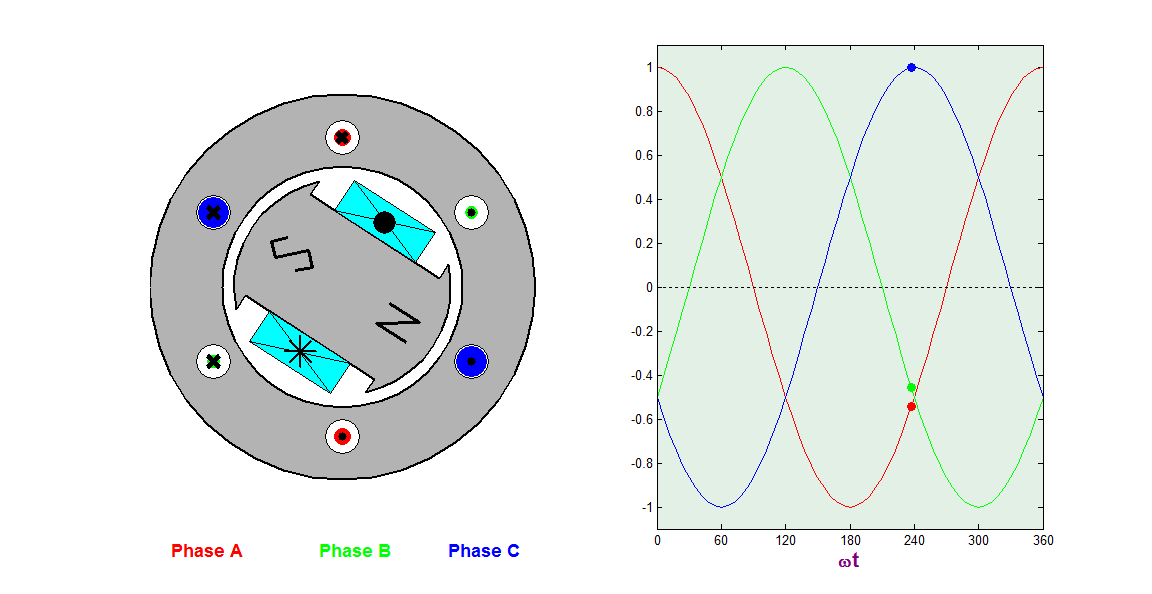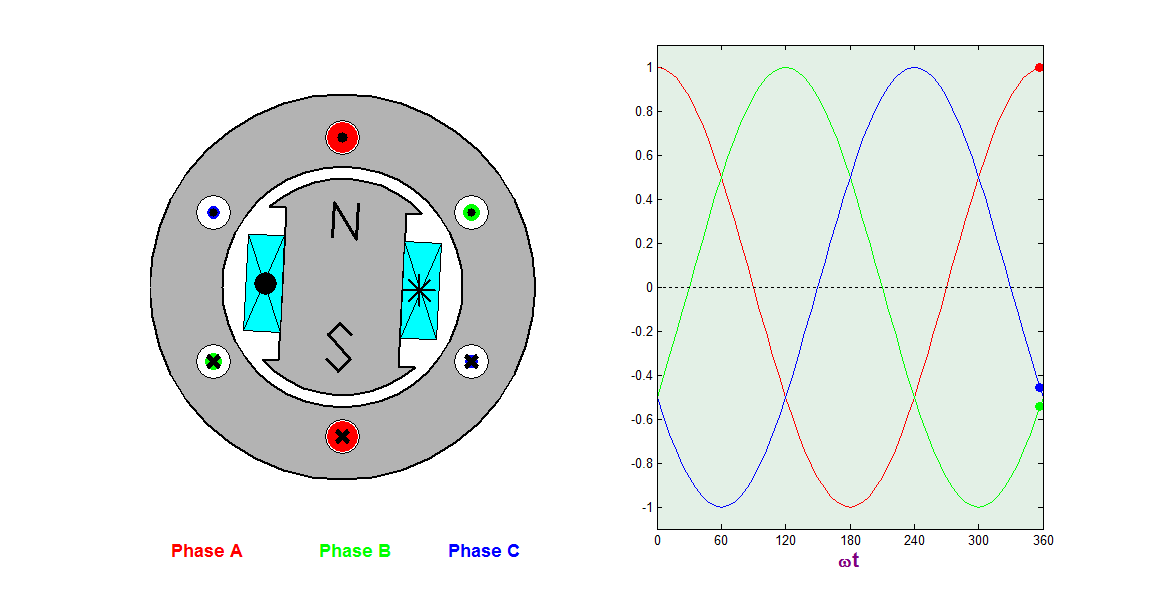
Éste es un ejemplo elemental de generador de corriente alterna. La corriente se obtiene por aplicación directa de la ley de Faraday
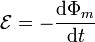
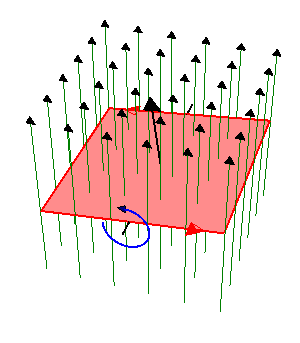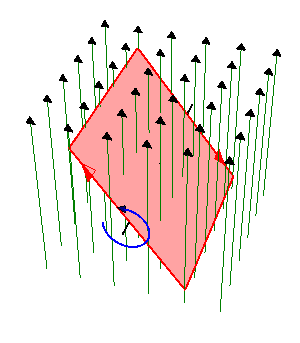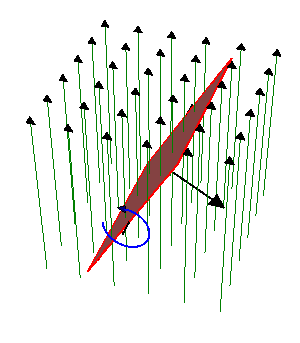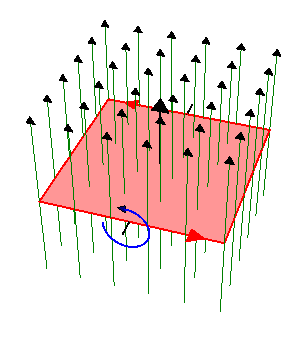
El flujo magnético es igual a
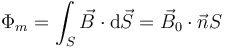
por ser 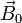 uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo
uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo
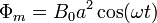
Derivando obtenemos la fuerza electromotriz.
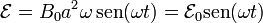
Vemos que este sistema se comporta como un generador de corriente alterna.
Un resultado generalizable es que esta f.e.m. es proporcional al área de la espira y a la frecuencia de giro. Por ello si, como ocurre en un avión, interesa reducir el tamaño del generador, es preciso aumentar su frecuencia.
Sustituyendo los valores numéricos
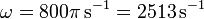
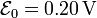
La corriente que circula por la espira es igual a
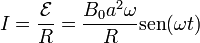
donde la resistencia vale
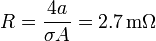
y la amplitud de la intensidad

3 Cálculo de la potencia
Podemos calcular la potencia disipada en el conductor por aplicación de la ley de Joule
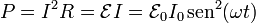
Esta potencia es oscilante, pero siempre positiva. La energía total disipada en un periodo es positiva
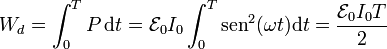
Sustituyendo los valores numéricos resulta, para la potencia máxima
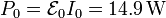
y para la energía disipada en un periodo
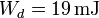
Este es un sistema en el que la potencia eléctrica producida en el generador es consumida en el propio generador (ya que la resistencia de la espira es una resistencia interna). En un generador real, la espira no es cerrada, sino que está conectada a un circuito externo, que es donde se consume la energía generada en la rotación.
4 Transformación de energía mecánica en eléctrica
Según hemos visto, en este sistema se está generando energía eléctrica, que es consumida en la propia espira o en el exterior. Ahora bien, ¿de dónde procede esta energía? No de la energía interna, ni de calor que entra. Por tanto, debe haber un flujo de trabajo entrante que iguale al saliente. Este trabajo entrante es el trabajo mecánico necesario para mantener la rotación de la espira.
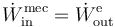
Para hacer los cálculos tomamos el eje Z en la dirección del campo magnético
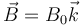
y que el eje de giro de la espira es el eje Y, de manera que su velocidad angular es

En este caso, al girar la espira, el vector normal a ella va girando en el plano XZ como
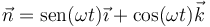
En cada instante la espira posee un momento magnético
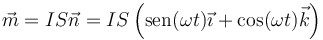
Sobre este momento dipolar, el campo magnético efectúa un par
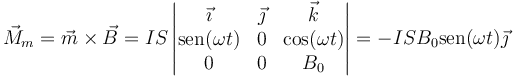
Para mantener la rotación a ritmo constante, el agente externo que hace girar la espira debe efectuar un par de fuerzas opuesto a este.
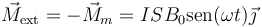
La potencia desarrollada por este par externo es igual a
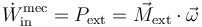
Sustituyendo el momento y la velocidad angular
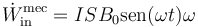
que es igual a

Este es el principio de un generador eléctrico como los que puede haber en una central hidroeléctrica o un aerogenerador. Un agente mecánico (agua, viento) hace girar una parte del generador (el rotor), lo que induce una corriente alterna (en el estátor), convirtiéndose energía mecánica en eléctrica. En los sistemas reales, no obstante, no es la espira la que gira en el campo magnético, sino el propio campo el que rota (haciéndose girar un imán) quedando estacionaria la espira.