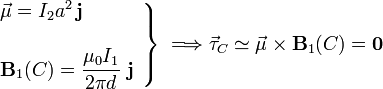Acción de corriente filiforme rectilínea sobre espira cuadrada (F2GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

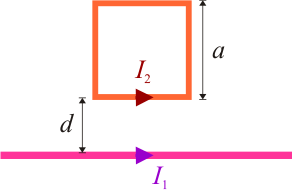
Determíne la fuerza resultante y el momento de fuerzas resultante que ejerce una corriente de intensidad

I 1

en un conductor filiforme de longitud indefinida, sobre una espira cuadrada coplanaria con él, recorrida por una intensidad de corriente

I 2

.

2 Solución

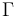Sean $\displaystyle \Delta$ un conductor rectilínea filiforme (de sección despreciable y longitud indefinida, y $\displaystyle\Gamma$ una espira conductora formada por cuatro segmentos rectilíneos filiformes de longitud $a$ . Consideraremos un sistema de referencia cartesiano tal que el conductor rectilíneo $\displaystyle \Delta$ coincide con el eje $O Z$ ; la espira está contenida en el plano $O X Z$ y su lado más próximo a $\displaystyle \Delta$ se encuentra a una distancia $d$ del conductor rectilíneo. Cuando $Δ$ y la espira $Γ$ son recorridas por sendas corrientes estacionarias $I 1$ e $I 2$ , aparece una interacción entre ambas que podemos calcular en términos del efecto que el campo magnético $\mathbf{B}_1 (\mathbf{r})$ creado por la corriente rectilínea ejerce sobre los elementos de corriente en la espira.

Dicho campo ha sido calculado con detalle en el ejercicio anterior, y que particularizaremos a los puntos de coordenadas $P (x,0, z)$ , que son los del plano $O X Z$ donde se encuentra la espira:

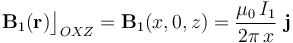
$\mathbf{B}_1(\mathbf{r})\big\rfloor_{OXZ}=\mathbf{B}_1(x,0,z)=\frac{\mu_0\!\ I_1}{2\pi\!\ x}\ \mathbf{j}$

2.1 Fuerza resultante sobre la espira

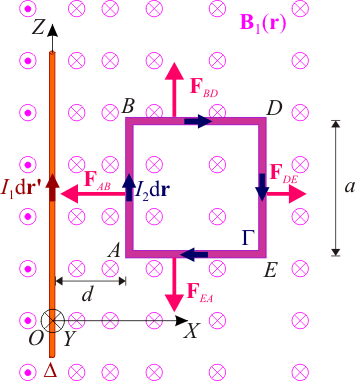
Los elementos van a ser distintos en cada tramo o segmento de espira, de manera que la fuerza resultante se puede obtener como la suma de las fuerzas sobre cada uno de los segmentos:

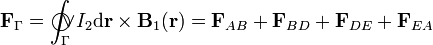
$\mathbf{F}_\Gamma=\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1(\mathbf{r})=\mathbf{F}_{AB}+\mathbf{F}_{BD}+\mathbf{F}_{DE}+\mathbf{F}_{EA}$

En todos los puntos del segmento $\overline{AB}$ el campo magnético creado por el hilo $Δ$ tiene idéntico valor, pues todo ellos están a igual distancia $d$ del hilo. La fuerza elemental sobre el elemento de corriente en este tramo es:

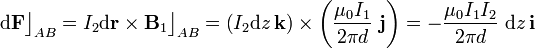
$\mathrm{d}\mathbf{F}\big\rfloor_{AB}=I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1\big\rfloor_{AB}=\left(I_2\mathrm{d}z\!\ \mathbf{k}\right)\times\left(\frac{\mu_0I_1}{2\pi d}\ \mathbf{j}\right)=-\frac{\mu_0 I_1I_2}{2\pi d}\ \mathrm{d}z\!\ \mathbf{i}$

Es decir, en todos los puntos del segmento $\overline{AB}$ se ejerce idéntica fuerza infinitesimal en la dirección perpendicular al hilo $Δ$ y al segmento de corriente $\overline{AB}$ . Óbservese que, como consecuencia de tener las corrientes el mismo sentido en ambos conductores (corrientes paralelas), cada elemento de corriente en $\overline{AB}$ es atraído por el hilo $Δ$ . Por otra parte, el campo creado por el hilo $Δ$ ejerce sobre el segmento $\overline{AB}$ una fuerza por unidad de longitud de valor constante,

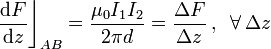
$\frac{\mathrm{d}F}{\mathrm{d}z}\bigg\rfloor_{AB}=\frac{\mu_0I_1I_2}{2\pi d}=\frac{\Delta F}{\Delta z}\,\mathrm{,}\,\;\;\forall\, \Delta z$

La fuerza total sobre el segmento de corriente comprendido entre los vérices $A$ y $B$ de la espira tendrá igual dirección y sentido que el de todas las fuerzas elementales. Por tanto, el segmento es atraído por el hilo con una fuerza cuya magnitud será igual a la anterior fuerza por unidad de longitud, multiplicada por la longitud total del segmento, $a$ :

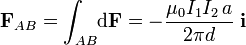
$\mathbf{F}_{AB}=\int_{AB}\!\mathrm{d}\mathbf{F}=-\frac{\mu_0I_1I_2\!\ a}{2\pi d}\ \mathbf{i}$

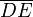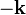En el segmento $\overline{DE}$ de la espira ocurre algo similar: el campo magnético es el mismo en todos sus puntos, aunque más débil que en $\overline{AB}$ al estar más alejado. Otra diferencia es que allí los elementos de corriente están orientados en el sentido de $-\mathbf{k}$ . El resultado es que sobre cada elemento de corriente y sobre todo el segmento $D E$ actúa una fuerza repulsiva ejercida por el hilo $Δ$ , al circular por ambos conductores corrientes eléctricas de sentido contrario (antiparalelas):

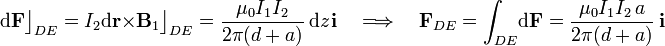
$\mathrm{d}\mathbf{F}\big\rfloor_{DE}=I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1\big\rfloor_{DE}=\frac{\mu_0 I_1I_2}{2\pi (d+a)}\ \mathrm{d}z\!\ \mathbf{i}\quad\Longrightarrow\quad\mathbf{F}_{DE}=\int_{DE}\!\mathrm{d}\mathbf{F}=\frac{\mu_0I_1I_2\!\ a}{2\pi (d+a)}\ \mathbf{i}$

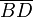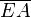En los segmentos $\overline{BD}$ y $\overline{EA}$ el campo magnético no es constante; sin embargo, éste será el mismo en los puntocs ocupados por sendos elementos de corriente,

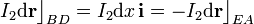
$I_2\mathrm{d}\mathbf{r}\big\rfloor_{BD}=I_2\mathrm{d}x\!\ \mathbf{i}=-I_2\mathrm{d}\mathbf{r}\big\rfloor_{EA}$

situados a igual distancia $x$ del hilo. En consecuencia, éste ejercerá sobre aquéllos fuerzas elementales opuestas:

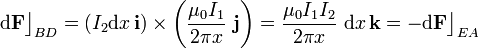
$\mathrm{d}\mathbf{F}\big\rfloor_{BD}=\left(I_2\mathrm{d}x\!\ \mathbf{i}\right)\times\left(\frac{\mu_0I_1}{2\pi x}\ \mathbf{j}\right)=\frac{\mu_0 I_1I_2}{2\pi x}\ \mathrm{d}x\!\ \mathbf{k}=-\mathrm{d}\mathbf{F}\big\rfloor_{EA}$

Al sumar todas estas fuerzas elementales, obtenemos las fuerzas totales que actúan sobre cada uno de los segmentos de corriente, y que serán también fuerzas opuestas:

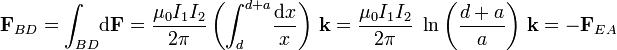
$\mathbf{F}_{BD}=\int_{BD}\!\mathrm{d}\mathbf{F}=\frac{\mu_0 I_1I_2}{2\pi}\left(\int_d^{d+a}\!\frac{\mathrm{d}x}{x}\right)\!\ \mathbf{k}=\frac{\mu_0 I_1I_2}{2\pi}\ \ln\left(\frac{d+a}{a}\right)\!\ \mathbf{k}=-\mathbf{F}_{EA}$

Finalmente, la suma de las fuerzas sobre los cuatro segmentos proporciona la fuerza resultante sobre la espira $Γ$ :

$\mathbf{F}_\Gamma=\mathbf{F}_{AB}+\mathbf{F}_{DE}+\underbrace{\mathbf{F}_{BD}+\mathbf{F}_{EA}}_{=\mathbf{0}}=-\frac{\mu_0I_1I_2\!\ a^2}{2\pi d(d+a)}\ \mathbf{i}$

Es decir, la espira recorrida por la intensidad $I 2$ en el sentido indicado en las figuras, es atraída por la corriente $I 1$ que recorre el conductor rectilíneo filiforme en el sentido postivo del eje $O Z$ .

2.2 Momento resultante sobre la espira

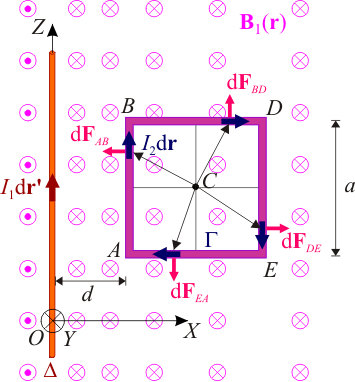
Si la espira se comporta como un sólido rígido, las ecuaciones de la dinámica se han de plantear tanto para la fuerza resultante, como para el momento resultante del sistema de fuerzas elementales distribuidas por toda la espira. Esta magnitud va a depender del punto respecto del cuál se calcule. Un punto que suele resultar especialmente interesante para realizar este cálculo es el centro geométrico $C$ de la espira (donde se cortan las dos diagonales):

$\vec{\tau}_C=\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\overrightarrow{CP}\times\mathrm{d}\mathbf{F}= \int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\big(\mathbf{r}-\mathbf{r}_C\big)\times\left[ I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1(\mathbf{r})\right]$

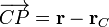donde $\overrightarrow{CP}=\mathbf{r}-\mathbf{r}_C$ es el vector que indica la posición arbitraria del elemento de corriente respeco del centro centro reducción $C$ .

Al igual que en el caso de la fuerza resultante, podemos obtener el momento resultante sobre la espira sumando los momentos parciales sobre cada uno de los segmentos. El momento elemental respecto de $C$ de la fuerza que ejerce el campo magnético 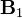$\mathbf{B}_1$ sobre un elemento de corriente en el segmento $\overline{AB}$ , es:

$\mathrm{d}\vec{\tau}_C\big\rfloor_{AB}=\left[(\mathbf{r}-\mathbf{r}_C)\times \mathrm{d}\mathbf{F}\right]_{AB}=-\frac{\mu_0I_1I_2}{2\pi d}\ (z-z_C)\mathrm{d}z\!\ \mathbf{j}$

... e integrando esta expresión a lo largo de dicho segmento, se obtiene que el momento es nulo:

$\vec{\tau}_C\big\rfloor_{AB}=\int_{AB}\!(\mathbf{r}-\mathbf{r}_C)\times \mathrm{d}\mathbf{F}=-\frac{\mu_0I_1I_2}{2\pi d}\left[ \int_{z_C-a/2}^{z_C+a/2}\!(z-z_C)\mathrm{d}z\right]\!\ \mathbf{j}=\mathbf{0}$

Idéntico resultado se obtiene en el segmento $D E$ :

$\vec{\tau}_C\big\rfloor_{DE}=\int_{DE}\!(\mathbf{r}-\mathbf{r}_C)\times \mathrm{d}\mathbf{F}=\frac{\mu_0I_1I_2}{2\pi (d+a)}\left[ \int_{z_C-a/2}^{z_C+a/2}\!(z-z_C)\mathrm{d}z\right]\!\ \mathbf{j}=\mathbf{0}$

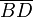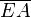En los segmentos $\overline{BD}$ y $\overline{EA}$ , los momentos elementales sobre elementos de corriente a igual distancia del hilo $Δ$ son opuestos (tal como ocurría con las fuerzas elementales). En consecuencia, los momentos respecto de $C$ de la fuerza magnética que actúa sobre dichos segmentos son no nulos pero opuestos:

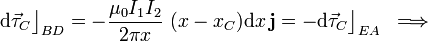
$\mathrm{d}\vec{\tau}_C\big\rfloor_{BD}=-\frac{\mu_0I_1I_2}{2\pi x}\ (x-x_C)\mathrm{d}x\!\ \mathbf{j}=-\mathrm{d}\vec{\tau}_C\big\rfloor_{EA}\;\;\Longrightarrow$

$\Longrightarrow\;\;\vec{\tau}_C\big\rfloor_{BD}=\frac{\mu_0I_1I_2}{2\pi}\left[ \int_{d}^{d+a}\!\frac{x_C-x}{x}\mathrm{d}x\right]\!\ \mathbf{j}=\frac{\mu_0I_1I_2}{2\pi}\left[\left(d+\frac{a}{2}\right)\ln\left(\frac{d+a}{d}\right)-a\right]\!\ \mathbf{j}=-\vec{\tau}_C\big\rfloor_{EA}$

En consecuencia, el momento resultante de la fuerza magnética sobre la espira, respecto del centro geométrico de ésta, es nulo:

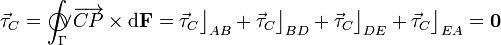
$\vec{\tau}_C=\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\overrightarrow{CP}\times\mathrm{d}\mathbf{F}=\vec{\tau}_C\big\rfloor_{AB}+\vec{\tau}_C\big\rfloor_{BD}+\vec{\tau}_C\big\rfloor_{DE}+\vec{\tau}_C\big\rfloor_{EA}=\mathbf{0}$

Sin embargo, calculado respecto de otro centro de reducción, el momento será distinto de cero. Puede comprobarse que respecto del vértice $A$ , por ejemplo, el momento resultante es:

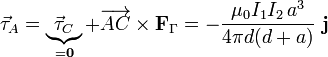
$\vec{\tau}_A=\underbrace{\vec{\tau}_C}_{=\mathbf{0}}+\overrightarrow{AC}\times\mathbf{F}_\Gamma=-\frac{\mu_0I_1I_2\!\ a^3}{4\pi d(d+a)}\ \mathbf{j}$

2.3 Caso de espira muy pequeña

En el caso de que las dimensiones de la espira sean mucho menores que la distancia que la separa del hilo $Δ$ que genera el campo, el cálculo de fuerza y momento resultantes se simplifican considerablemente. En esta situación puede considerarse que toda la espira es prácticamente un punto (el $C$ ), de manera que toda ella está sometida al mismo campo magnético. Por tanto, la fuerza resultante ejercida por el campo creado por el hilo sobre la espira va a ser prácticamente nula:

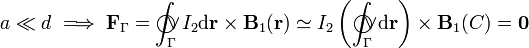
$a\ll d\;\Longrightarrow\;\mathbf{F}_\Gamma=\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1(\mathbf{r})\simeq I_2\left(\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\mathrm{d}\mathbf{r}\right)\times\mathbf{B}_1(C)=\mathbf{0}$

Y si la fuerza resultante es nula, el momento resultante será el mismo para cualquier centro de reducción. Por otra parte, si la espira es lo suficientemente pequeña, el par de fuerzas que actúa sobre ella es igual al producto vectorial del momento dipolar de la espira, 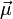$\vec{\mu}$ , por el valor del campo mangético en su posición:

$\vec{\tau}_C= \int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\big(\mathbf{r}-\mathbf{r}_C\big)\times\left( I_2\mathrm{d}\mathbf{r}\times\mathbf{B}_1\right)\simeq\left[ \frac{I_2}{2}\int_\Gamma\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \!\big(\mathbf{r}-\mathbf{r}_C\big)\times \mathrm{d}\mathbf{r}\right]\times\mathbf{B}_1(C)=\vec{\mu}\times\mathbf{B}_1(C)$

Como la espira es plana, el momento dipolar puede se calculado fácilmente: su módulo es igual a la intensidad de la corriente que la recorre multiplicado por el área de la figura plana limitada por la espira; tiene dirección perpendicular al plano que la contiene, y su sentido está determinado por el sentido en que la corriente recorre la espira, siguiendo el criterio del triedro directo. En el sistema bajo estudio, se tiene...

$\left.\begin{array}{l}\displaystyle\vec{\mu}=I_2a^2\!\ \mathbf{j}\\ \\ \displaystyle\mathbf{B}_1 (C)=\frac{\mu_0I_1}{2\pi d}\ \mathbf{j} \end{array}\right\}\;\Longrightarrow\vec{\tau}_C\simeq\vec{\mu}\times\mathbf{B}_1(C)=\mathbf{0}$

Acción de corriente filiforme rectilínea sobre espira cuadrada (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerza resultante sobre la espira

2.2 Momento resultante sobre la espira

2.3 Caso de espira muy pequeña

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES