Efecto Doppler
De Laplace
Contenido |
1 Introducción
Es un hecho conocido que cuando un vehículo, como una ambulancia, emite una señal de una determinada frecuencia y se encuentra en movimiento, para el conductor de la ambulancia, la frecuencia de la señal emitida permanece constante, mientras que para un observador exterior el sonido posee una frecuencia variable, siendo más agudo cuando la ambulancia se acerca, y más grave cuando se aleja.
Esto es una manifestación del efecto Doppler, (bautizado así en honor a Christian Doppler). Este efecto se encuentra también en el estudio de la radiación procedente de las galaxias, en los radares de carretera o aeropuertos o en los ultrasonidos de los murciélagos o delfines.
El principio general es:
- Si una fuente de las ondas se acerca a un observador, la frecuencia de las ondas que éste mide es mayor que la que mide el emisor. En el caso óptico, esto se denomina “corrimiento hacia el violeta” (o hacia el azul).
- Si la fuente se aleja del observador, éste mide una frecuencia menor que el emisor. Esto se denomina “corrimiento hacia el rojo”
2 Efecto Doppler para ondas sonoras
2.1 Caso de un observador en movimiento
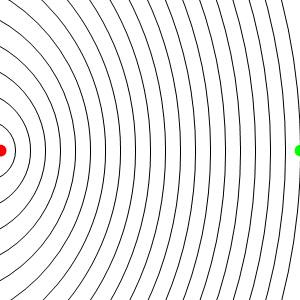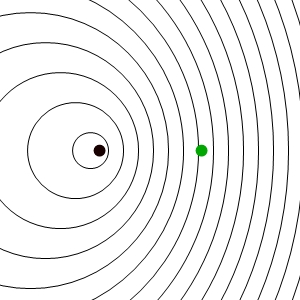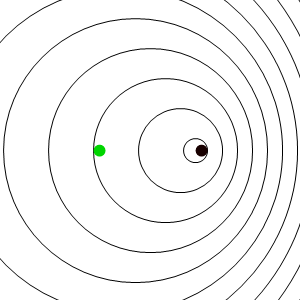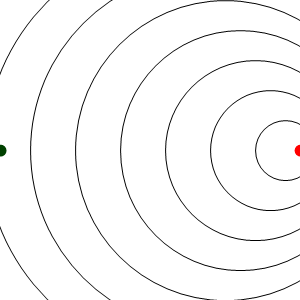
Consideremos en primer lugar el caso de una fuente en reposo respecto al medio circundante (el aire). Esta fuente emite ondas de frecuencia f, o equivalentemente, emite frentes de onda espaciadas un periodo T = 1 / f. Estas ondas se propagan el el aire radialmente con velocidad c. La distancia entre crestas sucesivas, en el sistema de la fuente, será λ = cT.
Queremos determinar la frecuencia que mide un observador que se acerca o se aleja radialmente de la fuente. Al estar la fuente, el observador y la dirección de propagación alineadas, podemos usar cantidades escalares, en lugar de vectoriales, y llamar v0 a la velocidad de este observador.
Tomaremos:
- vo < 0 si el observador se mueve hacia la posición que ocupa la fuente.
- vo > 0 si el observador se mueve en en el sentido que lo aleja de la fuente.
| vo > 0 | 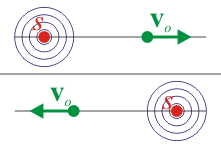
|
| vo < 0 | 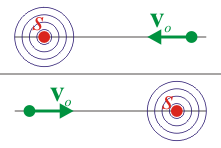
|
Cuando el observador se aleja de la fuente, los frentes llegan a él con un intervalo mayor que con el que fueron emitidos, ya que cada frente debe recorrer una distancia adicional para alcanzar al observador, la que éste ha recorrido en el tiempo intermedio.
Supongamos que una cresta llega al observador en un instante t. La siguiente llegará en un instante t + T', en este tiempo el observador ha recorrido una distancia
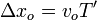
Este segundo frente llegó a la posición original del observador un tiempo T tras el anterior. Para alcanzar al observador debe recorrer la distancia que éste ha avanzado y para ello empleará un tiempo T' − T. Por tanto
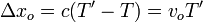
Despejando
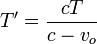
y la frecuencia medida por el observador es
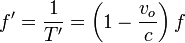
El observador mide una frecuencia menor cuando el observador se aleja, y una mayor cuando se acerca.
Podemos representar este resultado gráficamente. Trazando una gráfica en la que el eje de abscisas es la distancia a la fuente y el de ordenadas el tiempo, la fuente estacionaria aparece como una línea vertical. Los frentes de onda son líneas que se alejan de la fuente en ambos sentidos, con una pendiente T / λ = 1 / c. El observador que se aleja de la fuente será una línea oblicua, con una pendiente 1 / vo, mayor (esto es, más vertical) que la de los frentes de onda (si no, éstos no le alcanzarían). Considerando el triángulo señalado en la figura, obtenemos el resultado anterior.
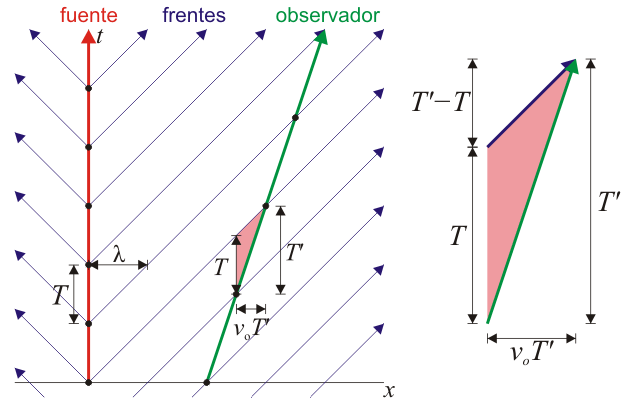
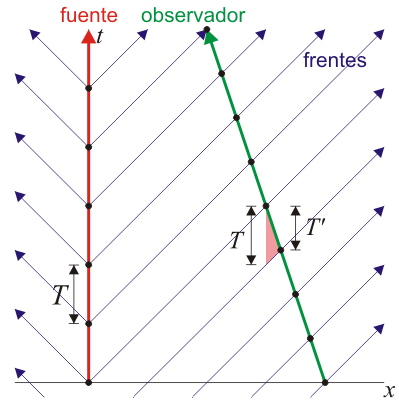
El mismo resultado se obtiene en el caso en que el observador se acerque a la fuente, solo que en ese caso el observador va al encuentro de los frentes de onda, y por tanto mide un periodo menor, y una frecuencia mayor.
En este caso tendríamos, de acuerdo con la figura
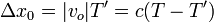

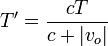

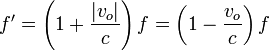
Matemáticamente la fórmula es la misma que antes, cuando se tiene en cuenta el signo de la velocidad del observador.
Por ejemplo supongamos que el medio es el aire y la velocidad del sonido es 340 m/s. Una fuente estacionaria emite una frecuencia de 440 Hz. Un observador se mueve hacia ella con una velocidad de 30 m/s. La frecuencia de la señal que mide este receptor es
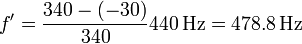
Esta frecuencia es mayor que la de emisión, porque el observador se acerca hacia la fuente y su velocidad es por tanto negativa.
2.2 Caso de una fuente en movimiento
Supongamos ahora el caso de una fuente en movimiento (a una velocidad vs inferior a la del sonido, c) y un observador en reposo.
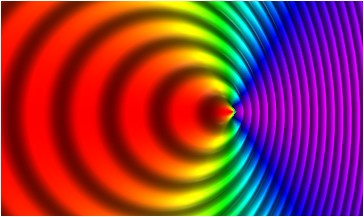
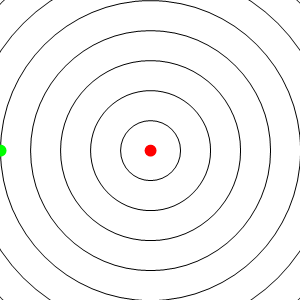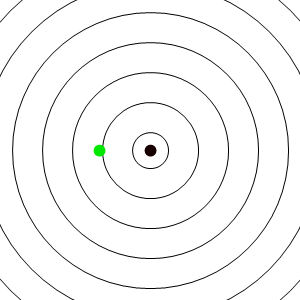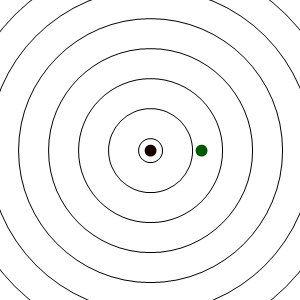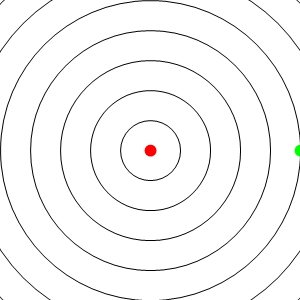
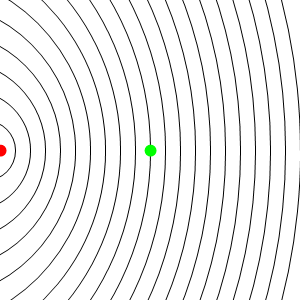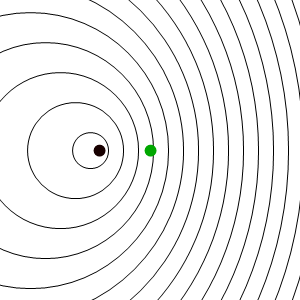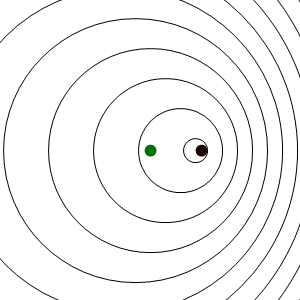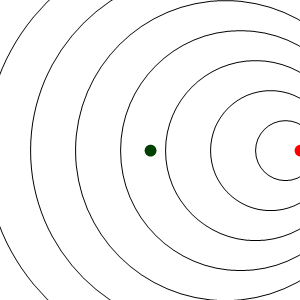
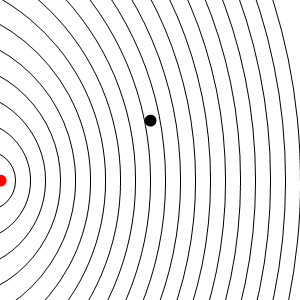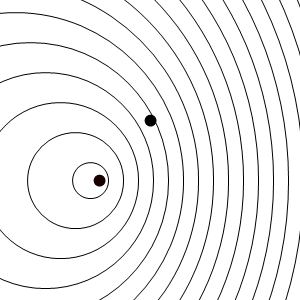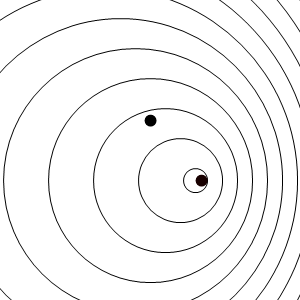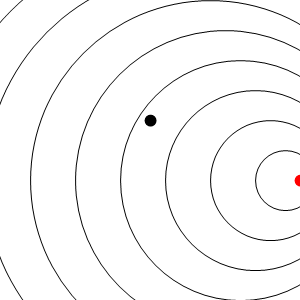
En este caso los frentes de onda se van emitiendo desde un punto que va avanzando, y por tanto se acumulan por la “proa”, mientras se enrarecen por la “popa”. El resultado es que un observador estacionario situado delante del emisor, mide una frecuencia de recepción mayor que la de emisión, mientras que uno situado por detrás mide una frecuencia menor.
Seguiremos el siguiente criterio de signos:
- vs > 0 si la fuente se dirige hacia la posición que ocupa el observador.
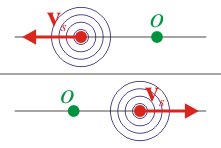
- vs < 0 si la fuente se dirige en sentido contrario a la posición que ocupa el observador.
(¡OJO! Este criterio es diferente del definido en el apartado anterior para la velocidad del observador. vs es una cosa y vo otra; la regla para tener claros los signos es que si se mueven el uno hacia el otro debe resultar una frecuencia recibida mayor que la emitida y al contrario si se alejan).
| vs > 0 | vs < 0 |
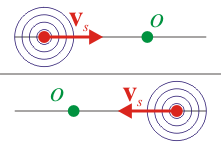
| 
|
Supongamos que el emisor avanza hacia el receptor con velocidad vs positiva, de forma que los frentes de onda se emiten en intervalos de T segundos y por tanto desde puntos espaciados vsT metros. Para llegar al receptor el primer frente debe recorrer una distancia X a una velocidad c, mientras que el segundo sólo recorrerá X − vsT (pero fue emitido un tiempo T más tarde). Empleando la construcción indicada en la figura tenemos que
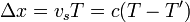

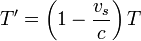

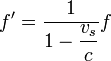
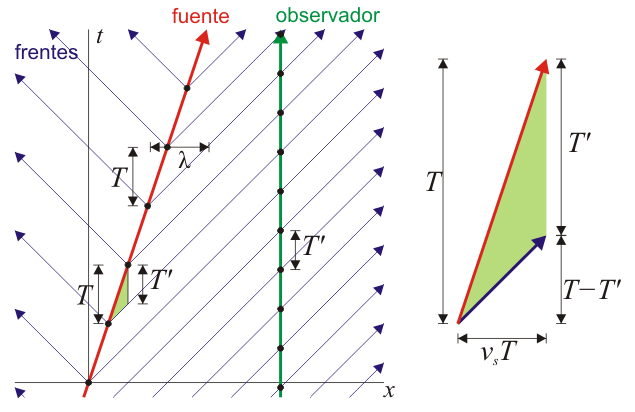
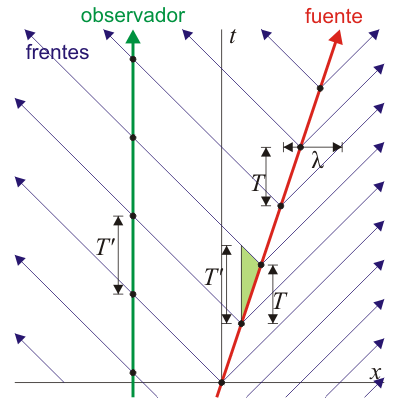
El mismo resultado se obtiene si el observador se encuentra a popa del emisor. En este caso el cálculo es
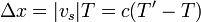

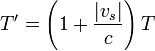

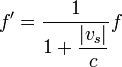
que coincide con el anterior si se considera que la velocidad es negativa cuando el emisor se aleja del receptor.
Hay que destacar que el efecto Doppler si el que se mueve es el emisor no coincide con el que resulta si el que se mueve es el observador.
Por ejemplo supongamos de nuevo el medio es el aire y la velocidad del sonido es 340 m/s. La fuente emite una frecuencia de 440 Hz y se mueve hacia un observador en reposo con una velocidad de 30 m/s. La frecuencia de la señal que mide el receptor es
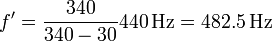
Esta frecuencia no coincide con la que se obtuvo en el apartado anterior para el caso de un observador que se acerca hacia la fuente estacionaria a esta misma velocidad.
2.3 Caso de que los dos estén en movimiento
Cuando tanto la fuente como el receptor se encuentran en movimiento respecto al medio, el efecto Doppler resultante será una combinación de los dos anteriores.
Podemos realizar el cálculo de dos formas sencillas:
- Relacionando directamente lo que mide el emisor con lo que mide el receptor, o
- Empleando un observador intermedio ficticio en reposo respecto al aire. Este observador se limitaría a reemitir las señales que le llegan. En este caso, tendríamos en primer lugar un efecto Doppler debido a una fuente móvil y un observador fijo, seguido de uno debido a una fuente fija y un observador móvil.
Empleando al observador intermedio, que mide un periodo Ti resulta un efecto Doppler que es el producto de los otros dos por separado.
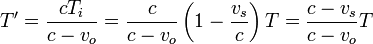

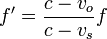
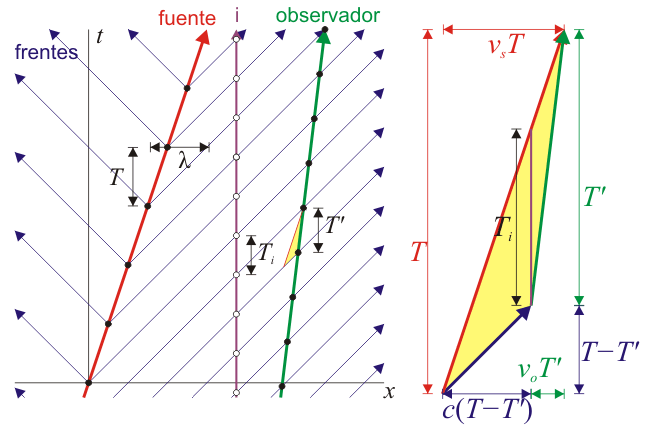
Sin recurrir al observador intermedio, empleamos la construcción indicada en la figura y vemos que se cumple la relación
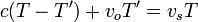

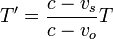

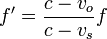
Esta fórmula es válida también si la fuente se aleja del observador o si el observador se acerca a la fuente, sin más que tener en cuenta los signos de las velocidades:
- La velocidad del observador es:
- Positiva, vo > 0, cuando el observador se mueve (respecto al medio) en el sentido que lo aleja de la fuente
- Negativa, vo > 0, cuando se mueve hacia la posición de la fuente
- La velocidad de la fuente es
- Positiva, vs > 0, cuando la fuente se mueve (respecto al medio) hacia la posición que ocupa el observador
- Negativa, vs < 0, cuando se mueve en el sentido que lo aleja del observador.
Para recordar los signos sólo hay que tener en cuenta que si fuente y el observador se acercan el uno al otro, la frecuencia debe aumentar, y si se alejan, debe disminuir (al contrario con el periodo).
Otra ayuda consiste en recordar que si ambos se mueven a la misma velocidad, de forma que la distancia entre ellos permanece constante, el efecto Doppler es nulo. Para este caso
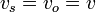

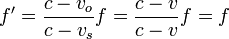
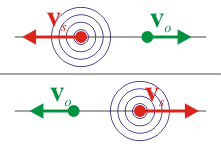
Gráficamente
| vs > 0 | vs < 0 | |
| vo > 0 | 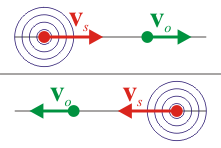
| 
|
| vo < 0 | 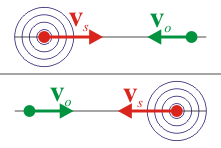
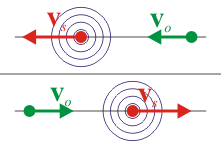
| 
|
Como ejemplo supongamos otra vez que el medio es el aire y la velocidad del sonido es 340 m/s. La fuente emite una frecuencia de 440 Hz y se mueve , respecto al aire, con una velocidad de 15 m/s hacia un observador que también se acerca a la fuente con una velocidad de 15 m/s respecto al aire. La frecuencia de la señal que mide el receptor es
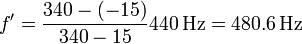
Esta frecuencia no coincide con ninguna de las dos obtenidas en los ejemplos anteriores, pese a que en todos los casos la velocidad relativa entre la fuente y el observador es la misma: se acercan con una velocidad de 30 m/s. Es muy importante recordar que lo que aparece en las fórmulas no es la velocidad relativa, sino la velocidad respecto al medio circundante.
2.4 Caso de velocidades oblicuas
La fórmula anterior para el caso de emisor y receptor presupone que ambos se mueven en línea recta el uno hacia el otro (o se alejan según la misma línea). Sin embargo, es posible que la velocidad de uno, de otro o ambos vaya según una dirección oblicua.
En este caso, la fórmula anterior se generaliza fácilmente, ya que solo la componente radial contribuye al efecto Doppler de las ondas sonoras. Por tanto, la fórmula general es
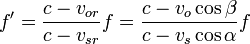
Siendo α y β los ángulos que las velocidades forman con la línea que une al emisor (en el momento en que se emitió la onda) y al receptor.
Si denominamos 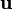 al vector unitario en la recta que une al emisor al receptor y sentido el que va del primero al segundo, la forma vectorial de esta ecuación es
al vector unitario en la recta que une al emisor al receptor y sentido el que va del primero al segundo, la forma vectorial de esta ecuación es
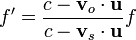
En el caso de que el movimiento sea oblicuo, el efecto Doppler depende del tiempo, ya que incluso aunque emisor y receptor se muevan uniformemente, el ángulo que forman las velocidades con la línea que les une va variando con el tiempo.
Por ejemplo, supongamos una fuente que se mueve uniformemente a lo largo de una recta y un observador en reposo, a una cierta distancia de esta recta. Podemos escribir sus posiciones y velocidades como
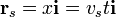
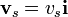
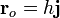
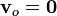
El vector unitario en la dirección emisor-receptor es
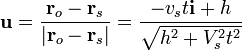
de forma que el efecto Doppler es
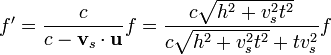
o, en términos de la posición ocupada por la fuente en el momento en que se emite la onda
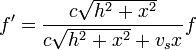
Representando gráficamente esta función vemos que, como es conocido de la experiencia, mientras el emisor se está acercando, la frecuencia recibida es mayor que la de emisión. Cuando pasa por delante del observador, se produce un cambio más o menos brusco de la frecuencia, pasando por frecuencias iguales justo cuando está delante, y cuando se aleja la frecuencia pasa a ser menor que la de emisión.
3 Efecto del viento
En todo lo anterior hemos supuesto que el aire por el que se propaga el sonido se encuentra en reposo. ¿Qué ocurre si está en movimiento?
Si se mueve rigidamente de forma uniforme, la generalización de las fórmulas anteriores es sencilla. Si conocemos las velocidades de la fuente 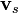 , el observador
, el observador 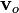 y el aire
y el aire 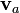 respecto a un sistema externo (como el suelo), basta con calcular previamente las velocidades del emisor y el receptor relativas al aire. Con esto, la fórmula general queda
respecto a un sistema externo (como el suelo), basta con calcular previamente las velocidades del emisor y el receptor relativas al aire. Con esto, la fórmula general queda
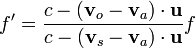
con las simplificaciones correspondientes si el movimiento es puramente radial o alguno de los agentes está en reposo.
Si el movimiento del aire no es uniforme o no homogéneo, el problema es mucho más complicado, ya que el efecto Doppler resulta dependiente tanto de la posición como del tiempo y ni siquiera las trayectorias del sonido se pueden suponer líneas rectas.
4 Fórmula empleando el movimiento relativo
Podemos expresar el efecto Doppler usando la notación del movimiento relativo estudiada en cinemática.
Supongamos un sistema “1” ligado al suelo y “0” rígidamente unido al aire (suponiendo que este se mueve como un bloque. El sistema “0” coincidirá con el “1” en el caso del aire inmóvil y se trasladará con una velocidad 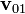 para todos los puntos (que sería
para todos los puntos (que sería 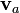 en la fórmula anterior).
en la fórmula anterior).
Suponemos que instantáneamente el origen de coordenadas tanto del sistema “0” como del “1” se encuentran en la posición en que estaba el emisor cuando se emitió la onda. En ese momento, el emisor se mueve respecto al aire con una velocidad 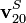 y respecto al suelo con una velocidad
y respecto al suelo con una velocidad 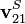 cumpliéndose
cumpliéndose

con “2” un sistema ligado al emisor. El receptor se encontrará en la posición relativa al punto de emisión 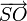 y moviéndose con velocidad
y moviéndose con velocidad 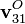 respecto al suelo y
respecto al suelo y 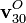 respecto al aire (con “3” un sistema ligado al receptor).
respecto al aire (con “3” un sistema ligado al receptor).
El vector unitario en la dirección que va del emisor al receptor será
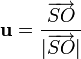
de forma que la expresión para el efecto Doppler queda (multiplicando por el módulo del vector de posición en el numerador y el denominador)
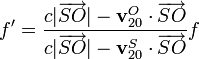
Por otro lado podemos considerar la velocidad del sonido como un vector, ya que el sonido que llega al receptor se propaga a lo largo de la línea que va del emisor al receptor. Este vector tiene módulo constante en el sistema “0”
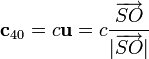
de forma que podemos escribir el efecto Doppler como
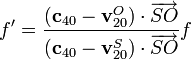
Esta fórmula nos dice que las magnitudes que realmente determinan el efecto Doppler son las velocidades del sonido relativas al emisor y al receptor.
Si los datos que nos dan son las velocidades del emisor, receptor y el aire, respecto al suelo, la formula habrá que cambiarla por
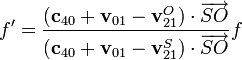
que podemos reescribir como
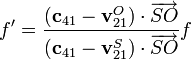
donde
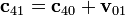
sería la velocidad del sonido respecto al suelo, suma vectorial de la que tiene respecto al aire más la de este respecto al suelo. Este es el efecto de arrastre que nos dice que las palabras se las lleva el viento.
5 Corrimiento en la frecuencia
A menudo el efecto Doppler es solo una pequeña corrección respecto a la frecuencia emitida, debido a que la velocidad de la fuente y del observador es pequeña comparada con la velocidad de la onda en el medio. En este caso, más informativo que dar la frecuencia absoluta, interesa dar el corrimiento en la frecuencia que es la diferencia entre la frecuencia medida por el observador y la emitida por la fuente
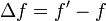
También se define el corrimiento relativo como el cociente entre esta cantidad y la frecuencia emitida
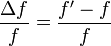
5.1 Caso del observador en movimiento
Sustituyendo la frecuencia medida por el observador
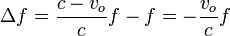

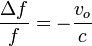
5.2 Caso de la fuente en movimiento
Si es la fuente la que se mueve, el corrimiento en la frecuencia es exactamente
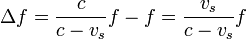
Si la velocidad de la fuente es muy pequeña comparada podemos despreciar vs frente a c, quedando el corrimiento en la frecuencia
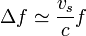

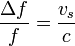
5.3 Caso de fuente y observador en movimiento
En este caso tenemos una combinación de los dos anteriores
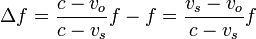
Despreciando de nuevo vs frente a c, si la velocidad de la fuente es pequeña
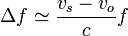

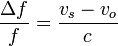
Vemos que, aunque el resultado completo para el efecto Doppler depende de las velocidades absolutas respecto al medio, tanto de emisor como de receptor, el corrimiento de frecuencias, cuando es pequeño, depende sólo de la velocidad relativa entre el emisor y el receptor, v = vo − vs.
5.4 Caso de movimiento oblicuo
Si las velocidades no son paralelas a la línea que une al emisor con el receptor, el corrimiento Doppler tiene la expresión
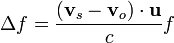
6 Efecto Doppler para la radiación electromagnética
El efecto Doppler también se aplica a la radiación electromagnética. Cuando una fuente emisora de ondas de luz o de radio se mueve respecto a un observador se produce una variación de la frecuencia medida. En el caso de la luz procedente de las galaxias, fue el descubrimiento del corrimiento hacia al rojo, lo que permitió averiguar la expansión del Universo.
El efecto Doppler para ondas de radio es la base del principio del funcionamiento de los radares, que permiten medir simultáneamente la posición y la velocidad de un vehículo que se mueve respecto a la torre de un aeropuerto.
No obstante, cuando se trata de ondas electromagnéticas, las expresiones dadas anteriormente dejan de ser correctas. La razón es que las fórmulas expuestas más arriba se deducen empleando las fórmulas clásicas de suma de velocidades, que son incorrectas para velocidades comparables a la de la luz (en particular, si una de las velocidades es justamente la de la luz). Para obtener la expresión correcta es preciso emplear la teoría de la relatividad. Esta teoría requiere que la velocidad de la onda (la luz) sea la misma para todos los observadores, y que las expresiones resultantes dependan solo de la velocidad relativa del observador respecto a la fuente y no de cada una por separado.
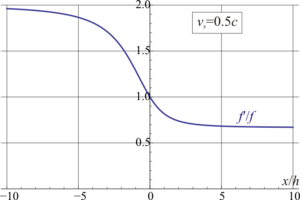
Cuando se emplean cálculos relativistas resulta la expresión para la frecuencia medida por el observador
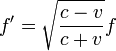
donde v es la velocidad con la que el observador se aleja de la fuente.
El corrimiento en la frecuencia será
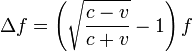
En la mayoría de los casos, la velocidad del observador o de la fuente es mucho menor que la de la luz, por lo que se puede puede hacer la expresión anterior se puede desarrollar en serie de Taylor en torno a v = 0 y resulta
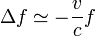
que es la misma fórmula que en el caso estudiado previamente para el sonido, considerando que v = vo − vs. Así pues, aunque las fórmulas completas son diferentes para el sonido y la luz, si estudiamos solo el corrimiento en la frecuencia para velocidades mucho menores que la de la onda, podemos emplear la misma expresión en los dos casos.
7 Efecto Doppler y reflexión de ondas
El efecto Doppler es el principio que usan los murciélagos para medir su propia velocidad o la de sus presas, así como la distancia a la que se encuentran de los obstáculos. También es la base de los radares tanto de carretera como en aeropuertos para medir la distancia y velocidad de vehículos en movimiento.
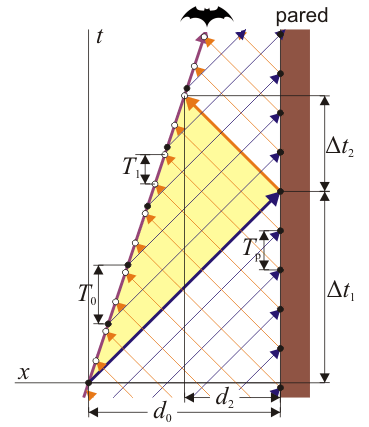
En el caso de un murciélago que se acerca a una pared tenemos un doble efecto Doppler. El murciélago emite señales de frecuencia f0 = 1 / T0 que llegan a la pared con una frecuencia fp = 1 / Tp dada por
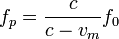
como corresponde a una fuente móvil y un receptor estacionario. Esta onda se refleja en la pared con la misma frecuencia fp y el murciélago recibe estos ecos con una frecuencia f1 = 1 / T1
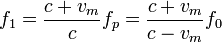
según la fórmula para un emisor fijo (la pared) y un receptor móvil, el propio murciélago. Ambos efectos Doppler incrementan la frecuencia de la señal. El resultado neto equivale a que el murciélago recibe las señales como si provinieran de un murciélago imagen que se acercara hacia él a la misma velocidad.
A partir de esta nueva frecuencia, se obtiene la velocidad del murciélago despejando.
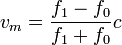
Conocida la velocidad y midiendo el intervalo total entre la emisión y la recepción Δt = Δt1 + Δt2 puede obtenerse la distancia a la pared en el momento de la recepción.
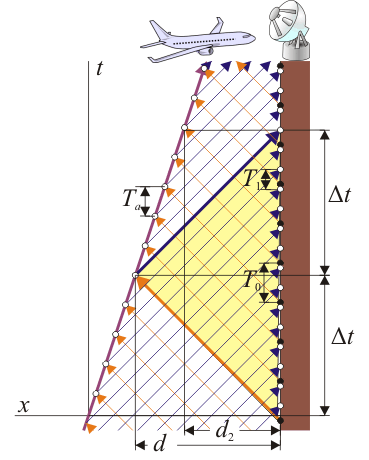
En el caso del radar de un aeropuerto el principio es exactamente es el mismo, solo que en este caso las ondas provienen de un radar fijo y rebotan en el avión en movimiento. Se emplean ondas electromagnéticas, por lo que lo correcto es emplear la fórmula que usa corrimiento de la frecuencia, ya que la velocidad del vehículo es minúscula comparada con la de la luz. En este caso, el corrimiento en la frecuencia que mide el avión es
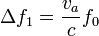
Estas ondas rebotan en el avión con la nueva frecuencia y llegan al radar con una frecuencia incrementada nuevamente en
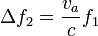
de forma que el incremento total en la frecuencia es aproximadamente
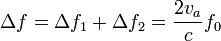
de donde la velocidad del vehículo medida por el radar es
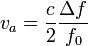
La distancia de la aeronave al aeropuerto se determina, como antes, a partir del tiempo de ida y vuelta de la señal.
Si en lugar de ondas electromagnéticas se usara sonido y la velocidad del vehículo fuera comparable a la del sonido, habría que usar las fórmulas completas, de forma análoga al caso del sónar del murciélago. El resultado es
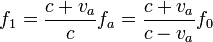

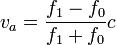
Si tanto la fuente como el espejo se encuentran en movimiento las fórmulas correspondientes se obtienen combinando las dos anteriores.