Velocidad y aceleración en tres dimensiones (GIOI)

De Laplace

Contenido

1 Velocidad
2 Aceleración
3 Triedro de Frenet
4 Cálculo de los diferentes elementos en un instante

1 Velocidad

1.1 Velocidad media

Se define la velocidad media como el cociente entre el desplazamiento en un intervalo de tiempo y la duración de dicho intervalo

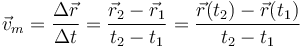
$\vec{v}_m = \frac{\Delta \vec{r}}{\Delta t} = \frac{\vec{r}_2-\vec{r}_1}{t_2-t_1}= \frac{\vec{r}(t_2)-\vec{r}(t_1)}{t_2-t_1}$

De la definición se desprende que:

La velocidad es un vector: posee dirección y sentido, no solo un módulo (por tanto, decir que la velocidad es de 120 km/h es una información incompleta).
Posee unidades de distancia dividida por tiempo, que en el sistema internacional serán m/s.
La velocidad media depende del desplazamiento neto entre dos puntos, por tanto en un movimiento cíclico la velocidad media es nula, pues el punto final e inicial coinciden, independientemente de la distancia que se haya recorrido.
La velocidad no es igual a espacio partido por tiempo, sino a un desplazamiento dividido por un intervalo, esto es, lo que cuenta no es el valor absoluto de la distancia o la hora que marca el reloj, sino cuánto ha cambiado la posición y cuánto tiempo se ha empleado en realizar dicho desplazamiento.

1.2 Velocidad instantánea

1.2.1 Definición y propiedades

De forma análoga al caso del movimiento rectilíneo definimos la velocidad instantánea como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero (se reduce a un instante)

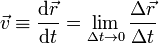
$\vec{v}\equiv\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{r}}{\Delta t}$

Matemáticamente, esto quiere decir que la velocidad instantánea es la derivada respecto al tiempo del vector de posición. En mecánica, una derivada respecto al tiempo suele representarse con un punto sobre la magnitud

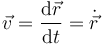
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \dot{\vec{r}}$

De esta definición se deduce que:

La velocidad instantánea es un vector: posee módulo, dirección y sentido.
Las unidades de la velocidad instantánea son la de una distancia dividida por un tiempo, en el SI m/s, aunque otras unidades como km/h son de uso frecuente.

1.2.2 Cálculo de la posición a partir de la velocidad

Si lo que conocemos es la velocidad, como función del tiempo, tenemos que en un intervalo de tiempo muy corto, $d t$ , se realiza un desplazamiento diferencial que es aproximadamente igual al producto de la velocidad por la duración del intervalo

$\mathrm{d}\vec{r}=\vec{v}\,\mathrm{d}t$

El desplazamiento durante un intervalo finito será la suma de todos los desplazamientos diferenciales

$\delta\vec{r}=\vec{r}_2-\vec{r}_1=\int_{\vec{r}_1}^{\vec{r}_2}\mathrm{d}\vec{r}=\int_{t_1}^{t_2}\vec{v}\,\mathrm{d}t$

Si consideramos que el instante inicial es $t 1 = 0$ y el final un instante $t$ cualquiera, queda la posición como función del tiempo

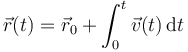
$\vec{r}(t)=\vec{r}_0 + \int_0^t \vec{v}(t)\,\mathrm{d}t$

1.3 Propiedades de la velocidad como vector

1.3.1 Dirección de la velocidad

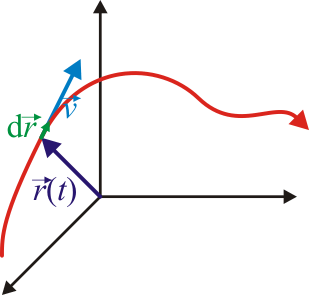
Un desplazamiento

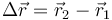
$\Delta\vec{r}=\vec{r}_2-\vec{r}_1$

es un vector que va del punto 1 al 2, ambos de la trayectoria de la partícula. Cuando este vector se multiplica por una cantidad escalar positiva, el resultado sigue siendo un vector con la misma dirección y sentido

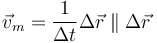
$\vec{v}_m=\frac{1}{\Delta t}\Delta \vec{r}\parallel \Delta \vec{r}$

Cuando la duración del intervalo se reduce a 0, los dos puntos se acercan hasta coincidir en el límite. En este caso, la dirección de la velocidad se convierte en tangente a la trayectoria.

La velocidad instantánea es un vector tangente a la trayectoria en cada punto.

1.3.2 Módulo (rapidez o celeridad)

Como todo vector, el vector velocidad instantánea posee un módulo, dirección y sentido, pudiendo escribirse en la forma

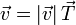
$\vec{v}=|\vec{v}|\,\vec{T}$

siendo $\vec{T}$ un vector unitario en la dirección y sentido de la velocidad, del que hablaremos más adelante.

En numerosas ocasiones no estamos interesados en la dirección y sentido de la velocidad, ya que sabiendo que es tangente a la trayectoria, podemos determinarlos geométricamente. En ese caso, la información necesaria se reduce al módulo de la velocidad, $|\vec{v}|$ . A esta cantidad se la conoce como rapidez (o celeridad):

Lo que en el habla cotidiana se denomina velocidad (“iba a 180 km/h”) es realmente una rapidez. Cuando la dirección y el sentido se dan por supuestos, la confusión entre los dos términos no es especialmente grave, pero siempre hay que tener en mente que la velocidad es realmente un vector, no un escalar.

1.3.3 Componentes cartesianas

En un sistema de referencia considerado como fijo, las componentes cartesianas de la velocidad vienen dadas por las derivadas respecto al tiempo de las componentes de la posición

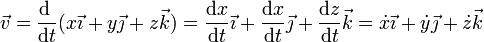
$\vec{v}=\frac{\mathrm{d}\ }{\mathrm{d}t}(x\vec{\imath}+y\vec{\jmath}+z\vec{k}) = \frac{\mathrm{d}x}{\mathrm{d}t}\vec{\imath}+\frac{\mathrm{d}x}{\mathrm{d}t}\vec{\jmath}+\frac{\mathrm{d}z}{\mathrm{d}t}\vec{k}=\dot{x}\vec{\imath}+\dot{y}\vec{\jmath}+\dot{z}\vec{k}$

o, separando por componentes

$v_x = \dot{x}\qquad v_y = \dot{y}\qquad v_z = \dot{z}$

Matemáticamente ello equivale a tratar el movimiento tridimensional como una combinación de tres movimientos unidimensionales. Por ello, podemos hallar cada componente de la posición integrando la componente de la velocidad correspondiente

$x = x_0 + \int_0^t v_x\,\mathrm{d}t\qquad y = y_0 + \int_0^t v_y\,\mathrm{d}t\qquad z = z_0 + \int_0^t v_x\,\mathrm{d}t$

1.3.4 Velocidad y ley horaria

Si tenemos el movimiento descrito en términos de la trayectoria y la ley horaria

$\vec{r}=\vec{r}(\theta)\qquad\qquad \theta=\theta(t)$

podemos hallar la velocidad en cada punto empleando la regla de la cadena

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}= \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,\frac{\mathrm{d}\theta}{\mathrm{d}t} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,\dot{\theta}$

Hay que resaltar que la velocidad es siempre la derivada de la posición respecto al tiempo, no respecto al primer parámetro que aparezca.

Velocidad en una circunferencia

Por ejemplo, imaginemos que se nos dice que una partícula describe la trayectoria circular

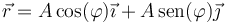
$\vec{r}=A\cos(\varphi)\vec{\imath}+A\,\mathrm{sen}(\varphi)\vec{\jmath}$

entonces su velocidad en cada punto será

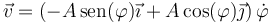
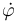$\vec{v} = \left(-A\,\mathrm{sen}(\varphi)\vec{\imath}+A\cos(\varphi)\vec{\jmath}\right)\dot{\varphi}$ y su valor dependerá de cómo cambie el ángulo con el tiempo, a través del factor $\dot{\varphi}\,$ . Si no se incluye este factor, el cálculo será erróneo.

1.4 Rapidez

Según hemos dicho, la rapidez o celeridad de un movimiento es lo que en el habla cotidiana se llama “velocidad”, pero en realidad es el módulo de ésta

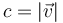
$c = \left|\vec{v}\right|$

Cuando la dirección y el sentido se dan por supuestos, la confusión entre los dos términos no es especialmente grave, pero siempre hay que tener en mente que la velocidad es realmente un vector, no un escalar.

1.4.1 Movimiento uniforme

La rapidez es la cantidad que nos informa del ritmo con el que se recorre la trayectoria. En particular, cuando la trayectoria (cualquiera que ésta sea) se recorre con rapidez constante, el movimiento se denomina movimiento uniforme.

$|\vec{v}| = \mathrm{cte} \qquad \Leftrightarrow\qquad \mbox{Movimiento uniforme}$

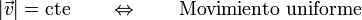
Así, por ejemplo, un movimiento circular uniforme no es un movimiento a velocidad constante, ya que aunque su módulo no varíe, su dirección y sentido cambian a lo largo de la trayectoria.

1.4.2 Unidades

La rapidez posee unidades de una distancia dividida por un tiempo. La unidad SI es el m/s, aunque otras unidades son de uso frecuente:

	m/s	km/h	mph	nudos
1 m/s =	1	3.6000	2.2369	1.9438
1 km/h =	0.2778	1	0.6214	0.5400
1 mph =	0.4470	1.6093	1	0.8690
1 nudo =	0.5144	1.8520	1.1508	1

Otra rapidez de uso frecuente en Física es la velocidad de la luz

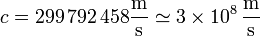
$c = 299\,792\,458 \frac{\mathrm{m}}{\mathrm{s}} \simeq 3\times 10^8\,\frac{\mathrm{m}}{\mathrm{s}}$

de forma que la celeridad de una partícula elemental suele expresarse como, por ejemplo, $v = 0.01 c$ , con lo que la velocidad de la luz funciona también como unidad de medida de velocidades

1.4.3 Relación con la distancia

La rapidez equivale a la velocidad con la que se recorre la distancia medida a lo largo de la curva

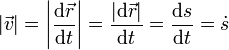
$|\vec{v}| = \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right| = \frac{|\mathrm{d}\vec{r}|}{\mathrm{d}t} = \frac{\mathrm{d}s}{\mathrm{d}t}=\dot{s}$

Esto quiere decir que, si conocemos la rapidez a lo largo de un movimiento, podemos determinar la distancia recorrida hasta un instante dado

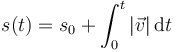
$s(t) = s_0 + \int_0^t |\vec{v}|\,\mathrm{d}t$

Ejemplo. Movimiento circular uniforme

Como ilustración supongamos el movimiento circular

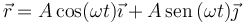
$\vec{r}=A\cos(\omega t)\vec{\imath} + A\,\mathrm{sen}\,(\omega t)\vec{\jmath}$

La rapidez la calculamos como el módulo de la velocidad

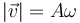
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}= -A\omega\,\mathrm{sen}\,(\omega t)\vec{\imath}+A\omega\cos(\omega t)\vec{\jmath}$ $\Rightarrow$ $|\vec{v}|=A\omega\,$

La distancia recorrida sobre la curva es entonces, suponiendo que empezamos a medir desde $t = 0$

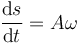
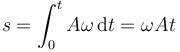
$\frac{\mathrm{d}s}{\mathrm{d}t}=A\omega$ $\Rightarrow$ $s =\int_0^t A\omega\,\mathrm{d}t = \omega A t$

Invirtiendo esta relación

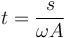
$t = \frac{s}{\omega A}$

podemos escribir la ecuación de la circunferencia en función de la distancia medida sobre ella.

$\vec{r}(s)=A\cos\left(\frac{s}{A}\right)\vec{\imath}+A\,\mathrm{sen}\left(\frac{s}{A}\right)\vec{\jmath}$

Este resultado debería ser evidente, ya que nos dice que cuando aumentamos el radio de la circunferencia, debemos recorrer una mayor distancia para girar el mismo ángulo.

1.4.4 Rapidez media

La rapidez (o celeridad) media de un movimiento en un intervalo es igual al cociente entre la distancia recorrida en dicho intervalo y su duración

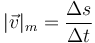
$|\vec{v}|_m = \frac{\Delta s}{\Delta t}$

Esta es la cantidad que se usa en el habla coloquial al referirse a la “velocidad media” (“hizo un promedio de 110 km/h”).

Hay que destacar que la rapidez media no es igual al módulo de la velocidad media.

Consideremos un piloto de Fórmula 1 que recorre los 300 km de una carrera en 1:30 h, llegando finalmente a la meta. En ese caso su celeridad media es 200 km/h, pero su velocidad media es nula (pues no hay desplazamiento; acaba donde empezó).

1.5 Dirección y sentido de la velocidad. Vector tangente

1.5.1 Definición

De la definición de velocidad se deduce que se trata de un vector siempre tangente a la trayectoria, ya que un desplazamiento infinitesimal a lo largo de la trayectoria es un vector en la dirección de esta. Esto nos permite definir un vector unitario tangente a la trayectoria normalizando la velocidad

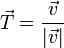
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}$

o, tal como dijimos antes,

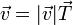
$\vec{v}=|\vec{v}|\vec{T}$

Puede demostrarse que el vector unitario tangente es independiente de la rapidez, esto es, que da igual que la trayectoria se recorra rápido o lento, el unitario tangente resultante es el mismo. Depende exclusivamente de la geometría de la trayectoria.

La única ambigüedad posible es el sentido. Dado que una misma curva puede recorrerse en un sentido o en el opuesto, existen dos posibles orientaciones para el vector tangente. Para un movimiento dado el unitario tangente siempre apunta en el sentido de avance de la partícula.

En un estado de reposo (instantáneo o permanente), 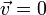$\vec{v}=0$ y el vector tangente no está definido.

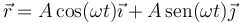
Por ejemplo, en el movimiento circular $\vec{r}=A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}(\omega t)\vec{\jmath}\,$

La velocidad, según vimos, es de la forma

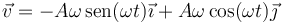
$\vec{v}=-A\omega\,\mathrm{sen}(\omega t)\vec{\imath}+A\omega\cos(\omega t)\vec{\jmath}\,$

siendo la rapidez el módulo de este vector

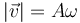
$|\vec{v}|=A\omega$

Dividiendo la velocidad por la rapidez hallamos el vector tangente

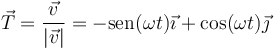
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\,$ Este vector es siempre tangente a la trayectoria circular. En este caso, además, es perpendicular al vector de posición, por tratarse de una circunferencia.

1.5.2 Recta tangente

El origen de la expresión “irse por la tangente” corresponde al caso de una partícula que abandona su movimiento curvo para seguir un movimiento rectilíneo con la velocidad que llevaba en el momento de abandonar la trayectoria original.

Si en un instante dado $t 1$ la partícula ocupa la posición 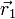$\vec{r}_1$ y se mueve con velocidad 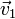$\vec{v}_1$ la recta tangente a la trayectoria se obtiene prolongando hacia adelante y hacia atrás en la dirección de la velocidad,

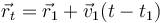
$\vec{r}_t=\vec{r}_1 + \vec{v}_1(t-t_1)$

Esta es la recta que seguiría una partícula que se moviera uniformemente y que pasara por el mismo punto y a la misma velocidad que la partícula real. Es el movimiento rectilíneo y uniforme que más se aproxima al real de la partícula en las proximidades del instante $t 1$ .

En muchas ocasiones, si no vamos a considerar instantes muy alejados de uno dado, puede ser más fácil trabajar con la recta tangente que con el movimiento auténtico, el cual puede ser muy complejo.

1.5.3 Movimiento rectilíneo

En tres dimensiones, un movimiento es rectilíneo se expresa diciendo que la dirección de la velocidad es constante (con posibles cambios de sentido). Esto equivale a que el vector tangente es constante (con posibles inversiones, como en el caso del movimiento armónico simple, que el sentido de movimiento va y viene, pero el movimiento es rectilíneo)

$\vec{T} = \mathrm{cte} \qquad \Leftrightarrow\qquad \mbox{Movimiento rectilíneo}$

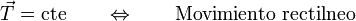
1.6 Movimiento rectilíneo y uniforme

Combinando los dos enunciados anteriores se tiene que, en tres dimensiones, un movimiento es rectilíneo y uniforme cuando el módulo de la velocidad es constante y cuando también lo es su dirección y sentido. Esto es, cuando la velocidad, como vector, es constante

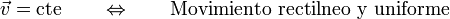
$\vec{v} = \mathrm{cte} \qquad \Leftrightarrow\qquad \mbox{Movimiento rectilíneo y uniforme}$

2 Aceleración

2.1 Definición

Se define la aceleración media como lo que varía la velocidad, dividido por el tiempo empleado en realizar el cambio

$\vec{a}_m = \frac{\Delta \vec{v}}{\Delta t}$

Del mismo modo que se define la velocidad instantánea como la derivada de la posición respecto al tiempo, se define la aceleración instantánea como la derivada de la velocidad respecto al tiempo

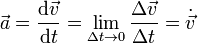
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{v}}{\Delta t}=\dot{\vec{v}}$

Esto quiere decir que la aceleración es la segunda derivada del vector de posición respecto al tiempo, lo que se indica con dos puntos sobre la magnitud

$\vec{a}=\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}=\ddot{\vec{r}}$

2.2 Unidades

La aceleración tiene unidades de velocidad dividida por tiempo, que en el SI será (m/s)/s = m/s².

Una magnitud con dimensiones de aceleración que es especialmente importante es la aceleración de la gravedad en la superficie terrestre, cuyo valor estándar es, por definición,

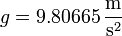
$g = 9.80665\,\frac{\mathrm{m}}{\mathrm{s}^2}$

de manera que muchas aceleraciones se expresan como múltiplos de esta unidad, aunque dichas aceleraciones no estén relacionadas con la gravedad.

2.3 Componentes cartesianas

Considerando que la base $\{\vec{\imath},\vec{\jmath},\vec{k}\}$ es fija, resulta que las componentes cartesianas de la aceleración son las derivadas temporales de las componentes de la velocidad (y segundas derivadas de las de la posición)

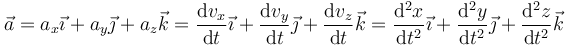
$\vec{a}=a_x\vec{\imath}+a_y\vec{\jmath}+a_z\vec{k}=\frac{\mathrm{d}v_x}{\mathrm{d}t}\vec{\imath}+\frac{\mathrm{d}v_y}{\mathrm{d}t}\vec{\jmath}+\frac{\mathrm{d}v_z}{\mathrm{d}t}\vec{k}=\frac{\mathrm{d}^2x}{\mathrm{d}t^2}\vec{\imath}+\frac{\mathrm{d}^2y}{\mathrm{d}t^2}\vec{\jmath}+\frac{\mathrm{d}^2z}{\mathrm{d}t^2}\vec{k}\,$

o, separando por componentes

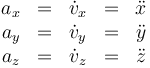
$\begin{array}{ccccc} a_x & = & \dot{v}_x & = & \ddot{x} \\ a_y & = & \dot{v}_y & = & \ddot{y} \\ a_z & = & \dot{v}_z & = & \ddot{z} \end{array}\,$

Cuando se separa un movimiento en sus componentes, puede verse como la superposición de tres movimientos rectilíneos.

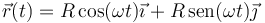
Así, por ejemplo, el movimiento $\vec{r}(t)=R\cos(\omega t)\vec{\imath} +R\,\mathrm{sen}(\omega t)\vec{\jmath}\,$

se descompone como

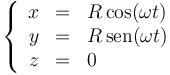
$\left\{ \begin{array}{rcl} x & = & R\cos(\omega t)\\ y & = & R\,\mathrm{sen}(\omega t)\\ z & = & 0\end{array}\right.\,$

siendo las componentes cartesianas de su aceleración

$\left\{ \begin{array}{rcl} a_x = \ddot{x} & = & -R\omega^2\cos(\omega t) = -\omega^2 x\\ a_y = \ddot{y} & = & -R\omega^2\,\mathrm{sen}(\omega t)=-\omega^2y\\ a_z = \ddot{z} & = & 0\end{array}\right.\,$ y por tanto, puede verse como la superposición de dos movimientos armónicos simples. Sin embargo, el resultado no es un un m.a.s. (que es un movimiento rectilíneo), sino un movimiento circular, según hemos dicho.

2.4 Cálculo de la velocidad y la posición

Si conocemos la aceleración en todo instante

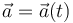
$\vec{a}=\vec{a}(t)$

y las condiciones iniciales

$\vec{r}_0 = \vec{r}(t=0)\qquad\qquad\vec{v}_0 = \vec{v}(t=0)$

podemos determinar la velocidad en cada instante integrando una vez

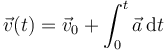
$\vec{v}(t) = \vec{v}_0+\int_0^t \vec{a}\,\mathrm{d}t$

y la posición integrando una segunda vez

$\vec{r}(t) = \vec{r}_0+\int_0^t\vec{v}\,\mathrm{d}t$

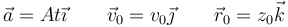
Así, por ejemplo, si $\vec{a}=At\vec{\imath}\qquad \vec{v}_0=v_0\vec{\jmath}\qquad \vec{r}_0=z_0\vec{k}\,$

La velocidad en cada instante es

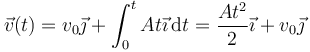
$\vec{v}(t) = v_0\vec{\jmath}+\int_0^t A t\vec{\imath}\,\mathrm{d}t=\frac{At^2}{2}\vec{\imath}+v_0\vec{\jmath}\,$

y la posición

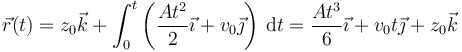
$\vec{r}(t) = z_0\vec{k}+\int_0^t \left(\frac{At^2}{2}\vec{\imath}+v_0\vec{\jmath}\right)\,\mathrm{d}t=\frac{At^3}{6}\vec{\imath}+v_0t\vec{\jmath}+z_0\vec{k}\,$

2.4.1 Caso de una aceleración constante

En el caso de que la aceleración sea constante en el tiempo, la integración de la ecuación anterior es inmediata

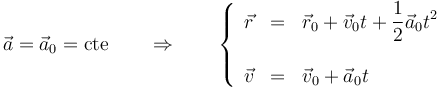
$\vec{a}=\vec{a}_0=\mathrm{cte}\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\vec{r}& = & \displaystyle \vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{a}_0t^2 \\ && \\ \vec{v}& = & \vec{v}_0+\vec{a}_0t\end{array}\right.$

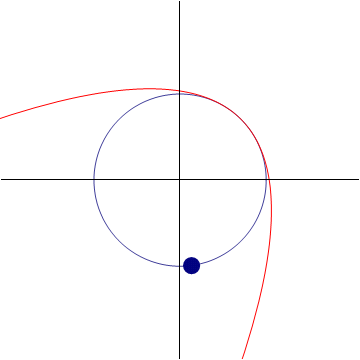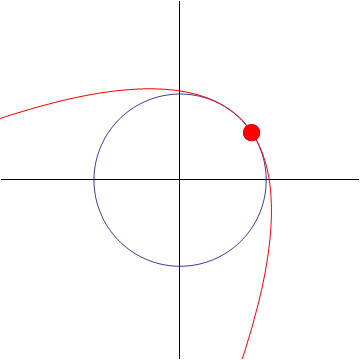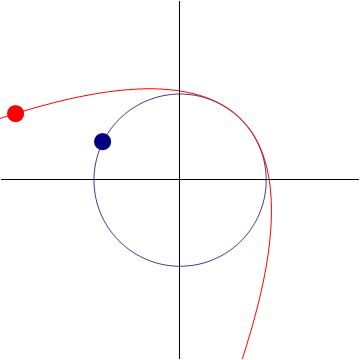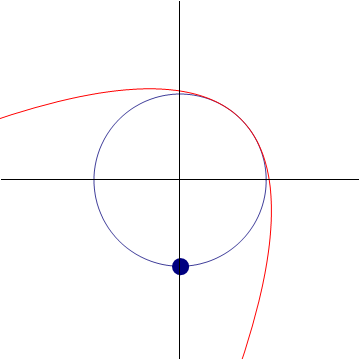
2.4.2 Aproximación parabólica

Cuando conocemos la posición 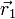$\vec{r}_1$ , la velocidad 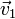$\vec{v}_1$ y la aceleración 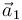$\vec{a}_1$ del movimiento, podemos hallar cuál sería el movimiento de aceleración constante que más se aproxima al movimiento real en ese instante

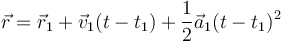
$\vec{r} = \vec{r}_1+\vec{v}_1(t-t_1)+\frac{1}{2}\vec{a}_1(t-t_1)^2$

Esta es una aproximación muy buena para el movimiento real si no nos alejamos mucho del instante de tangencia. Representa una mejora sobre la aproximación lineal (la recta tangente) vista anteriormente.

De manera análoga pueden hallarse aproximaciones de tercer grado, de cuarto… Cada una será más precisa que la anterior, pero requerirá más términos y por tanto más cálculos.

2.5 Componentes intrínsecas

A diferencia de la velocidad, la aceleración puede formar un ángulo cualquiera con la trayectoria.

Podemos escribir entonces el vector aceleración como suma de dos componentes, una en la dirección de movimiento, tangente a la velocidad, y un resto perpendicular a ella. Estas dos componentes se denominan aceleración tangencial y aceleración normal. Estas son las denominadas componentes intrínsecas de la aceleración.

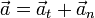
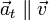
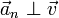
$\vec{a}=\vec{a}_t+\vec{a}_n\,$ $\vec{a}_t\parallel\vec{v}$ $\vec{a}_n\perp\vec{v}$

Hay que destacar que la aceleración tangencial y la normal son vectores, no cantidades escalares. No obstante, también se denominan usualmente de la misma manera a las componentes escalares, dado por supuesto la dirección y el sentido.

2.5.1 Expresiones algebraicas

A partir del doble producto vectorial, pueden hallarse expresiones para la componente tangencial y la componente normal de la aceleración

Aceleración tangencial

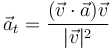
$\vec{a}_t = \frac{(\vec{v}\cdot\vec{a})\vec{v}}{|\vec{v}|^2}$

o, usando el vector unitario tangente a la trayectoria

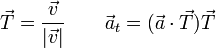
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}\qquad \vec{a}_t = (\vec{a}\cdot\vec{T})\vec{T}$

Si solo deseamos la componente escalar en la dirección del vector tangente

$a_t = \vec{a}\cdot\vec{T}=\frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}$

Aceleración normal: Puesto que la suma de la aceleración tangencial y la normal nos da el vector aceleración, podemos despejar

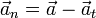
$\vec{a}_n = \vec{a}-\vec{a}_t$

Podemos calcularla directamente empleando el doble producto vectorial

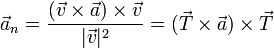
$\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}=(\vec{T}\times\vec{a})\times\vec{T}$

Si solo deseamos el valor de la componente escalar

$a_n = \sqrt{a^2-a_t^2}=\frac{|\vec{v}\times\vec{a}|}{|\vec{v}|}$

2.5.2 Interpretación física

Las componentes intrínsecas de la aceleración poseen interpretación física, además de la puramente algebraica.

Sabemos que la velocidad, como vector, posee módulo (la rapidez) y dirección y sentido (expresados por el vector unitario tangente)

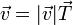
$\vec{v}=|\vec{v}|\vec{T}$

En el movimiento rectilíneo la aceleración sólo indica una cosa: el cambio en la rapidez, así que no hay ambigüedad en decir que un objeto se acelera, o se desacelera o frena.

En dos y tres dimensiones, en cambio decir que un cuerpo se acelera, puede referirse a dos conceptos, no incompatibles:

Que cambia la rapidez con que se mueve el cuerpo
Que cambia la dirección de movimiento

Ambos fenómenos implican un cambio en la velocidad y por tanto una aceleración.

Para separar los dos conceptos derivamos respecto la tiempo la expresión de la velocidad en función de la celeridad y el vector tangente

$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(|\vec{v}|\vec{T}\right) = \frac{\mathrm{d} \ }{\mathrm{d}t}\left(|\vec{v}|\right)\vec{T}+|\vec{v}|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}$

El primer término apunta en la dirección tangencial. Podemos demostrar que el segundo es perpendicular a ella, por el ser el vector tangente de módulo constante

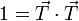
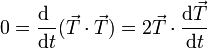
$1 = \vec{T}\cdot\vec{T}$ $\Rightarrow$ $0=\frac{\mathrm{d}\ }{\mathrm{d}t}(\vec{T}\cdot\vec{T})=2\vec{T}\cdot\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}$

Puesto que el producto escalar es nulo, ambos vectores son perpendiculares. En consecuencia

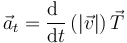
$\vec{a}_t = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(|\vec{v}|\right)\vec{T}$ $\vec{a}_n = |\vec{v}|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}$

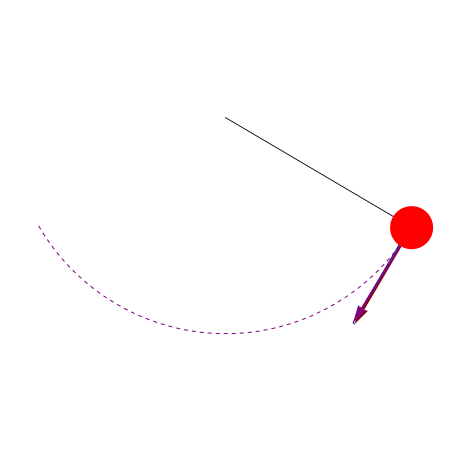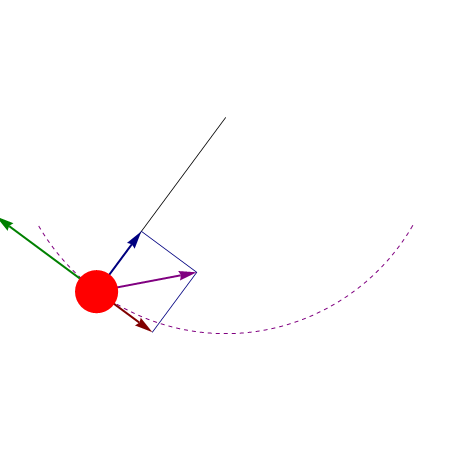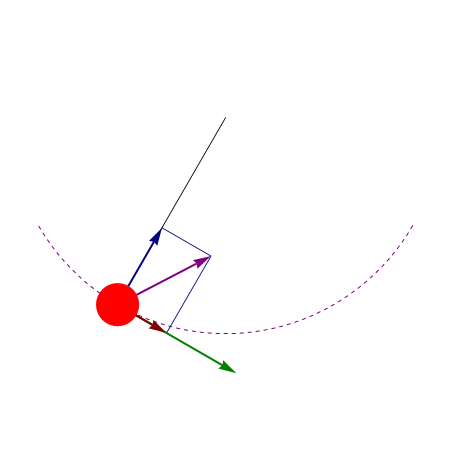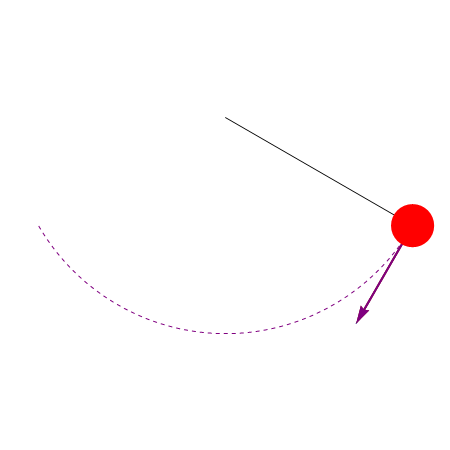
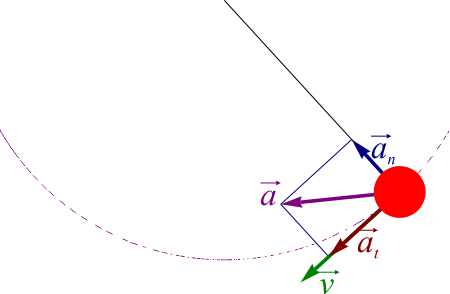
Por tanto:

Aceleración tangencial: Mide la variación en la rapidez, esto es, si la partícula pasa a moverse más rápido o más lento a lo largo de la trayectoria. La condición para que un movimiento sea uniforme es que la aceleración tangencial sea cero.

$\mbox{Movimiento uniforme}\qquad\qquad \Leftrightarrow \qquad\qquad \vec{a}_t=\vec{0}\quad\forall t$

Un movimiento en el que la componente tangencial de la aceleración permanece constante en el tiempo (esto es, su rapidez varía uniformemente) se denomina uniformemente acelerado.

$\mbox{Movimiento uniformemente acelerado}\qquad\qquad \Leftrightarrow \qquad\qquad a_t=\mathrm{cte}\quad\forall t$

Aceleración normal: Mide el cambio en la dirección del movimiento (el giro del vector tangente). La condición para que un movimiento sea rectilíneo es que la aceleración normal sea nula en todo instante

$\mbox{Movimiento rectilineo}\qquad\qquad \Leftrightarrow \qquad\qquad \vec{a}_n=\vec{0}\quad\forall t$

2.5.3 Vector normal

A partir de la aceleración normal podemos definir un vector normal a la trayectoria

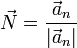
$\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}$

Como el vector unitario tangente, el unitario normal es una propiedad puramente geométrica y no depende de la rapidez con que se recorra la trayectoria.

Este vector apunta siempre hacia el “interior” de la curva, esto es, nos indica hacia donde cambia la dirección del movimiento.

Es fácil ver esta propiedad en el caso bidimensional. Si la partícula se mueve en el plano OXY el vector tangente se puede poner de la forma

$\vec{T}=\cos(\phi)\vec{\imath}+\mathrm{sen}(\phi)\vec{\jmath}$

siendo $\phi\,$ el ángulo que el vector tangente forma con el eje OX. Derivando esta expresión respecto al tiempo queda

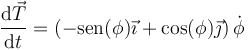
$\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}=\left(-\mathrm{sen}(\phi)\vec{\imath}+\cos(\phi)\vec{\jmath}\right)\dot{\phi}$

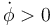El vector entre paréntesis es efectivamente ortogonal a $\vec{T}$ y forma un ángulo de 90° a la izquierda de éste. Si $\dot{\phi}>0$ la trayectoria se está curvando hacia la izquierda y hacia allí apunta la derivada. Si en cambio se curva hacia la derecha 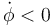$\dot{\phi}<0$ y esta derivada forma un ángulo de −90° con $\vec{T}$ . En ambos casos la derivada va hacia el interior de la curva, Normalizando este vector

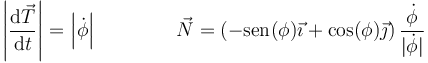
$\left|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}\right|=\left|\dot{\phi}\right|\qquad \qquad \vec{N}=\left(-\mathrm{sen}(\phi)\vec{\imath}+\cos(\phi)\vec{\jmath}\right)\frac{\dot{\phi}}{|\dot{\phi}|}$

donde el último factor no es más que el signo de la derivada 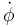$\dot{\phi}$

Hay que remarcar que el vector normal, como el vector tangente, depende de la posición.

2.5.4 Radio de curvatura

La aceleración normal puede escribirse en la forma

$\vec{a}_n = \frac{|\vec{v}|^2}{R}\vec{N}$

donde $R (t)$ es el llamado radio de curvatura de la trayectoria en ese instante. Este radio de curvatura es el radio de la llamada circunferencia osculatriz que es la que describiría una partícula que se moviera circularmente y tal que en ese instante ocupara la misma posición, tuviera la misma velocidad y la misma aceleración que la partícula real. El centro de esta circunferencia (centro de curvatura) está en cada instante en

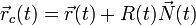
$\vec{r}_c(t) = \vec{r}(t)+R(t)\vec{N}(t)$

La curva formada por los sucesivos centros de curvatura se denomina evoluta de la trayectoria.

De nuevo, se puede dar una interpretación simple a este resultado en dos dimensiones. Antes se vio que

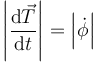
$\left|\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}\right|=\left|\dot{\phi}\right|$

siendo $\phi\,$ el ángulo con el eje OX. Su derivada temporal es una velocidad angular, representa el ritmo con el que está girando el vector tangente. Esta velocidad angular se relaciona con la velocidad lineal y el radio de giro como

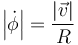
$\left|\dot{\phi}\right| = \frac{|\vec{v}|}{R}$

con lo que la derivada del vector tangente es

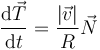
$\frac{\mathrm{d}\vec{T}}{\mathrm{d}t} = \frac{|\vec{v}|}{R}\vec{N}$

y la aceleración

$\vec{a}=\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}\vec{T}+\frac{|\vec{v}|^2}{R}\vec{N}$

Un movimiento circular es entonces aquel que tiene radio y centro de curvatura constantes.

A partir de la expresión vectorial de la aceleración normal podemos obtener el radio de curvatura como

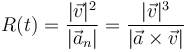
$R(t) = \frac{|\vec{v}|^2}{|\vec{a}_n|}= \frac{|\vec{v}|^3}{|\vec{a}\times\vec{v}|}$

A pesar de que esta expresión se calcula empleando la velocidad y la aceleración, que son específicas para cada movimiento concreto, el radio de curvatura y el centro de curvatura son propiedades puramente geométricas, independientes de la rapidez.

La inversa del radio de curvatura es la curvatura de la trayectoria

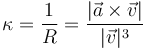
$\kappa=\frac{1}{R}=\frac{|\vec{a}\times\vec{v}|}{|\vec{v}|^3}$

La curvatura, como el radio de curvatura, mide cuánto se dobla la trayectoria. Una curva muy cerrada posee un radio de curvatura pequeño y una curvatura grande. Una curva suave posee radio de curvatura grande y curvatura reducida. En particular una trayectoria rectilínea (que tiene aceleración normal nula) posee una curvatura igual a cero (y un radio de curvatura infinito).

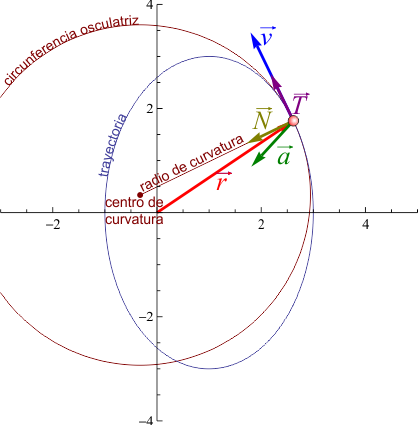
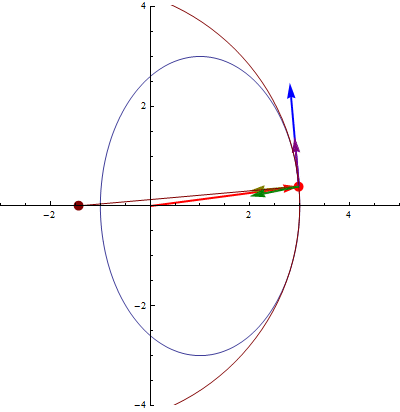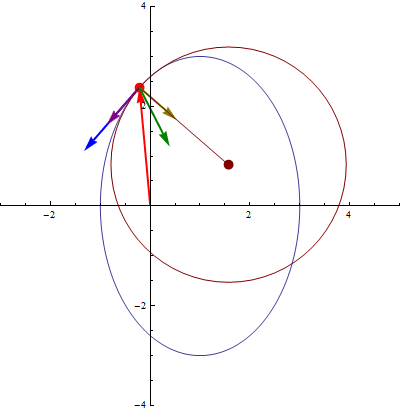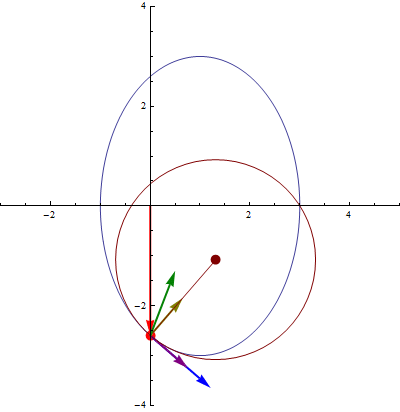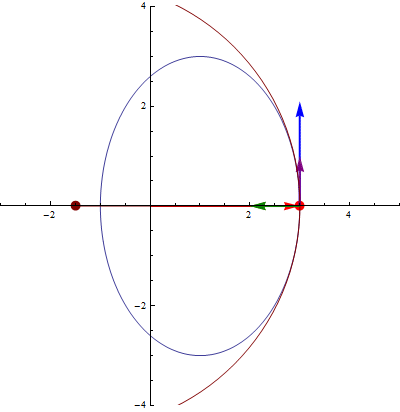
3 Triedro de Frenet

En los apartados anteriores hemos definido dos vectores unitarios relacionados de forma directa con la trayectoria:

Vector tangente: Unitario tangente a la trayectoria, que es el unitario en la dirección y sentido de la velocidad

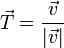
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}$

Vector normal: Unitario en la dirección y sentido de la aceleración normal

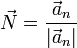
$\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}$

Estos dos vectores son unitarios y ortogonales entre sí. Por ello, se pueden emplear como los dos primeros vectores de una base vectorial ortonormal. Esta base es el llamado triedro de Frenet, constituido por estos dos vectores y un tercero:

Vector binormal: Unitario ortogonal a $\vec{T}$ y a $\vec{N}$ según la regla de la mano derecha

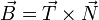
$\vec{B}=\vec{T}\times\vec{N}$

El vector binormal es también ortogonal a la trayectoria, pero también a la aceleración. Apunta en la dirección ortogonal al plano definido por $\vec{v}$ y $\vec{a}$ , por lo que también se puede hallar directamente a partir de estas dos magnitudes

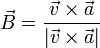
$\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}$

Esto hace que lo más fácil sea calcular en primer lugar el vector tangente, luego el binormal y por último el vector normal como

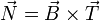
$\vec{N}=\vec{B}\times\vec{T}$

lo que da la expresión para el vector normal

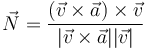
$\vec{N}=\frac{(\vec{v}\times\vec{a})\times \vec{v}}{|\vec{v}\times\vec{a}||\vec{v}|}$

El triedro de Frenet es un triedro móvil. Acompaña a la partícula en su movimiento y por tanto a la hora de derivar las expresiones en esta base habrá que tener en cuenta la dependencia temporal.

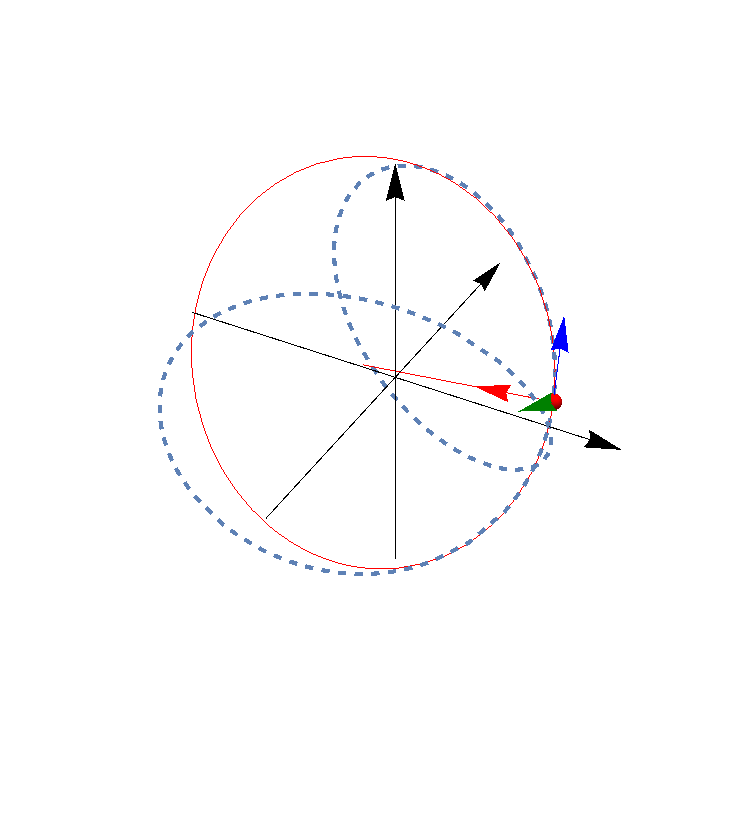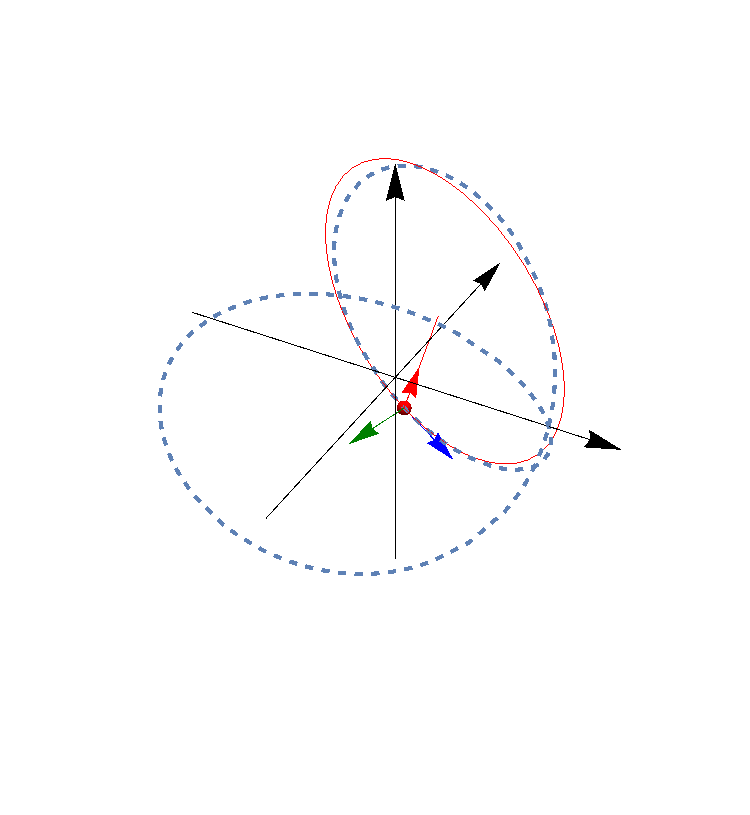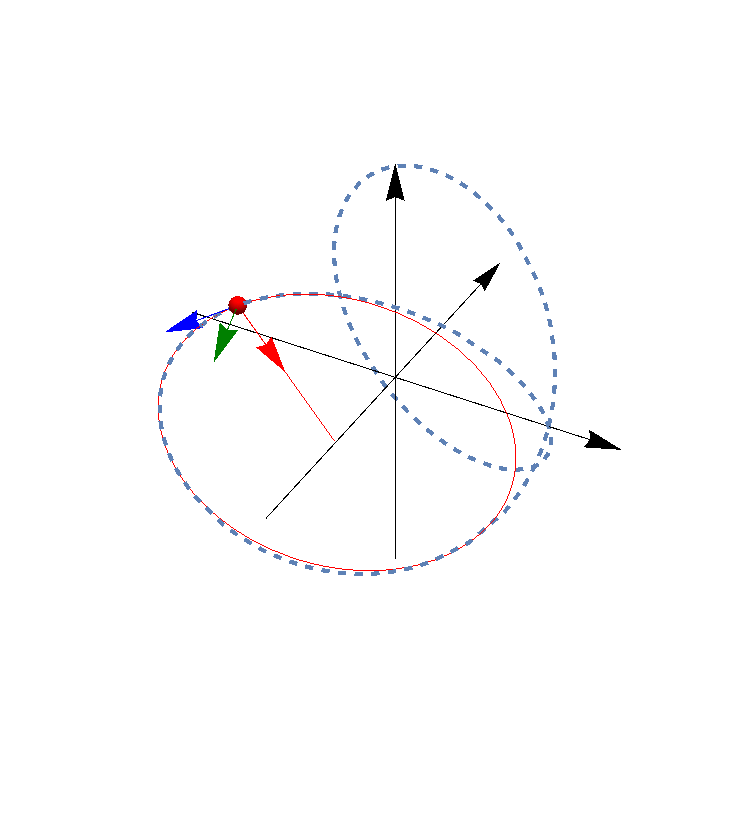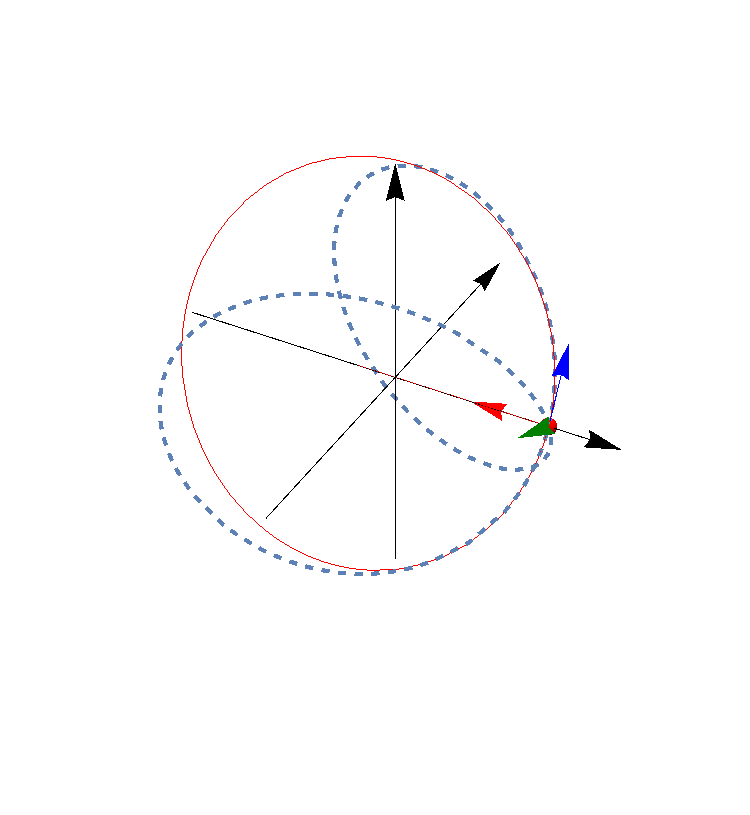
En esta animación el vector azul es el tangente, el rojo el normal y el verde el binormal.

Al constituir una base ortonormal dextrógira, cualquier vector podrá escribirse como combinación lineal de este triedro. De hecho, ya conocemos dos de estas expresiones

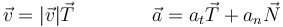
$\vec{v}=|\vec{v}|\vec{T}\qquad\qquad \vec{a}=a_t\vec{T}+a_n\vec{N}$

Una fuerza aplicada podrá tener componentes en las tres direcciones

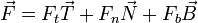
$\vec{F}=F_t\vec{T}+F_n\vec{N}+F_b\vec{B}$

En el caso de un movimiento circular, la velocidad y la aceleración angulares son ortogonales a la velocidad y aceleración lineales, por lo que apuntan en la dirección del vector binormal.

$\vec{\omega}=\omega\vec{B}\qquad\qquad \vec{\alpha}=\alpha\vec{B}$

Los vectores tangente y normal definen un plano (ortogonal al vector binormal) que es el que más se aproxima al movimiento de la partícula (conocido como plano osculador). Cuando el movimiento es estrictamente plano, quiere decir que el plano osculador coincide con el plano de movimiento y por tanto el vector binormal es constante

$\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}=\mathrm{cte}\qquad\Leftrightarrow\qquad\mbox{movimiento plano}$

El plano osculador será en general una función del tiempo. Así, en un movimiento helicoidal, irá girando con la partícula.

4 Cálculo de los diferentes elementos en un instante

De lo anterior se deduce que, conocida la posición como función del tiempo, 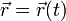$\vec{r}=\vec{r}(t)$ , puede calcularse el resto de magnitudes.

No obstante, a menudo no se dispone de una función sino, por medidas experimentales o por otras razones, de los valores de la posición $\vec{r}$ , la velocidad $\vec{v}$ y la aceleración $\vec{a}$ , en un instante dado. En este caso no podemos calcular ninguna derivada (que requiere conocer la dependencia temporal). ¿Quiere esto decir que no podemos hallar la aceleración tangencial, por ejemplo? No. De hecho, empleando los resultados anteriores, podemos calcular los valores de casi todas las magnitudes para ese instante.

Datos	Rapidez	Vector tangente	Aceleración tangencial (vector)	Aceleración tangencial (escalar)
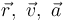
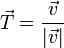
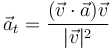
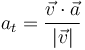
$\vec{r},\ \vec{v},\ \vec{a}$	$\|\vec{v}\|$	$\vec{T}=\frac{\vec{v}}{\|\vec{v}\|}$	$\vec{a}_t=\frac{(\vec{v}\cdot\vec{a})\vec{v}}{\|\vec{v}\|^2}$	$a_t=\frac{\vec{v}\cdot\vec{a}}{\|\vec{v}\|}$
Aceleración normal (vector)	Aceleración normal (escalar)	Vector normal	Radio de curvatura	Centro de curvatura
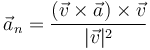
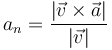
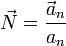
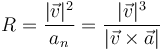
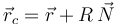
$\vec{a}_n=\frac{(\vec{v}\times\vec{a})\times\vec{v}}{\|\vec{v}\|^2}$	$a_n=\frac{\|\vec{v}\times\vec{a}\|}{\|\vec{v}\|}$	$\vec{N}=\frac{\vec{a}_n}{a_n}$	$R = \frac{\|\vec{v}\|^2}{a_n}=\frac{\|\vec{v}\|^3}{\|\vec{v}\times\vec{a}\|}$	$\vec{r}_c = \vec{r}+R\,\vec{N}$

Como vemos, ninguno de estos cálculos requiere hallar ninguna derivada.