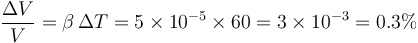Test de la Segunda Convocatoria 2015-2016

De Laplace

Contenido

1 Dipolo en campo eléctrico
2 Propiedades del equilibrio electrostático
3 Efecto de un campo magnético variable
4 Campo de dos superficies esféricas
5 Circuito triangular
6 Calentamiento de agua
7 Condensador con dos capas
8 Espira que entra en campo magnético
- 8.1 Pregunta 1
- 8.2 Pregunta 2
9 Proceso adiabático
10 Trabajo perdido
11 Dilatación de esfera

1 Dipolo en campo eléctrico

Un dipolo eléctrico cuyo momento dipolar vale 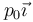$p_0 \vec{\imath}$ se encuentra inmerso en el campo eléctrico uniforme 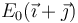$E_0 (\vec{\imath}+\vec{\jmath})$ . El efecto de este campo sobre el dipolo es producir…

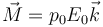
A un momento $\vec{M}=p_0 E_0 \vec{k}$
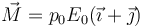
B un momento $\vec{M}=p_0 E_0 (\vec{\imath}+\vec{\jmath})$
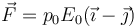
C una fuerza $\vec{F}=p_0 E_0 (\vec{\imath}-\vec{\jmath})$
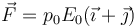
D una fuerza $\vec{F}=p_0 E_0 (\vec{\imath}+\vec{\jmath})$

Solución

La respuesta correcta es la A.

En un campo uniforme, el efecto sobre un dipolo es producir un par de fuerzas que tiende a alinearlo con el campo. El momento de este par es

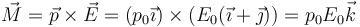
$\vec{M}=\vec{p}\times\vec{E}=(p_0\vec{\imath})\times\left(E_0(\vec{\imath}+\vec{\jmath})\right)=p_0E_0\vec{k}$

2 Propiedades del equilibrio electrostático

¿Cuál de las siguientes no es una propiedad general de un conductor en equilibrio electrostático?

A El potencial eléctrico es nulo en todos los puntos del conductor.
B El campo eléctrico en el interior del conductor es nulo.
C La densidad volumétrica de carga es nula.
D El campo eléctrico justo fuera del conductor es ortogonal a la superficie de éste.

Solución

La respuesta correcta es la A.

En el equilibrio electrostático el potencial eléctrico tiene el mismo valor en todos los puntos del conductor, pero este valor no tiene por qué ser cero.

3 Efecto de un campo magnético variable

Si en una región del espacio tenemos un campo magnético dependiente del tiempo, ¿cuál de las siguientes propiedades sigue siendo cierta en general?

A Las líneas de campo eléctrico no pueden ser cerradas.
B El flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada por ella.
C La integral del campo eléctrico entre dos puntos es independiente del camino.
D Puede definirse el potencial eléctrico.

Solución

La respuesta correcta es la B.

La ley de Gauss, que es lo que describe la opción B, es válida en todo momento, haya campos variables o no.

Para las otras tres opciones, de acuerdo con la ley de Faraday, cuando hay un campo magnético variable se induce una fuerza electromotriz

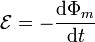
$\mathcal{E}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

siendo la fuerza electromotriz igual a

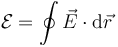
$\mathcal{E}=\oint \vec{E}\cdot\mathrm{d}\vec{r}$

Si la integral sobre una curva cerrada no es cero, esto quiere decir que la integral entre dos puntos depende del camino (ya que la suma de la ida y la vuelta no da 0), lo que impide definir el potencial eléctrico (que se basa en que no dependa del camino) y además permite que haya líneas de campo cerradas.

4 Campo de dos superficies esféricas

Dos superficies esféricas cargadas de radios $b$ y $2 b$ son concéntricas. La carga de la esfera interior vale $4 n C$ y la de la exterior $- 2 n C$ . Producen un campo radial 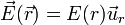$\vec{E}(\vec{r})=E(r)\vec{u}_r$ ¿Cuál de las siguientes es la gráfica correcta de $E (r)$ como función de la distancia al centro?

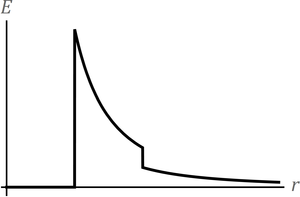
A	B


C	D

Solución

La respuesta correcta es la A.

De acuerdo con la ley de Gauss, el flujo del campo eléctrico es proporcional a la carga encerrada. Si la distribución tiene simetría esférica, el campo es de la forma

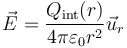
$\vec{E}=\frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\vec{u}_r$

En este caso,

para $r < b$ no encerramos ninguna, el flujo es cero y el campo es nulo.
Para $b < r < 2 b$ encerramos la esfera interior, que almacena una carga positiva, por tanto el flujo es positivo, el campo va hacia afuera y $E (r)$ es uuna función positiva.
Para $r > 2 b$ encerramos la esfera exterior y la interior, por lo que la carga encerrada es 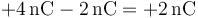$+4\,\mathrm{nC}-2\,\mathrm{nC} = +2\,\mathrm{nC}$ que, por ser positiva, implica un flujo positivo y un valor de $E (r)$ también positivo.

5 Circuito triangular

Se tiene el sistema de resistencias, condensadores y fuentes de voltaje de la figura.

5.1 Pregunta 1

¿Cuánto vale la corriente que entra por cada nodo?

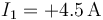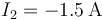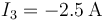
A $I_1=+4.5\,\mathrm{A}$ , $I_2=-1.5\,\mathrm{A}$ , $I_3=-2.5\,\mathrm{A}$
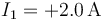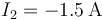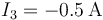
B $I_1=+2.0\,\mathrm{A}$ , $I_2=-1.5\,\mathrm{A}$ , $I_3=-0.5\,\mathrm{A}$
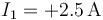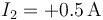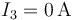
C $I_1=+2.5\,\mathrm{A}$ , $I_2=+0.5\,\mathrm{A}$ , $I_3=0\,\mathrm{A}$
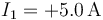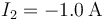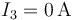
D $I_1=+5.0\,\mathrm{A}$ , $I_2=-1.0\,\mathrm{A}$ , $I_3=0\,\mathrm{A}$

Solución

La respuesta correcta es la B.

Por la rama horizontal de abajo no circula corriente ya que contiene un condensador, por el cual no puede pasar la corriente continua (en medio hya vacío o un dieléctrico, que impide el paso de carga). Por tanto, la única corriente circula por las dos ramas oblicuas.

Entre el nodo 1 y el 2 hay una diferencia de potencial de 12V, siendo la resistencia de esa rama 6Ω, por lo que por ella fluye una intensidad de corriente de 2A. Esta corriente entra por el nodo a mayor potencial (el 1) y sale por el 2. Luego 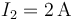$I_2=2\,\mathrm{A}$ .

Esto ya nos permite identificar la respuesta correcta, pero podemos hallar las otras dos intensidades. Entre el nodo 2 y el 3 hay una diferencia de potencial de 3V, por lo que por esa rama circula una corriente de 0.5A.

Por tanto, por el nodo 2 salen 2A y entran 0.5, es decir, salen 1.5 y queda 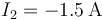$I_2=-1.5\,\mathrm{A}$ .

Por el nodo 3 sale la corriente que fluye del 2 al 3, es decir 0.5A y da 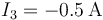$I_3=-0.5\,\mathrm{A}$ .

5.2 Pregunta 2

¿Cuánta potencia se consume en el sistema de resistencias?

A 31.5W
B 39W
C 25.5W
D 63W

Solución

La respuesta correcta es la C.

Una vez que tenemos las intensidades podemos hallar la potencia disipada como

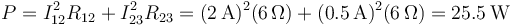
$P = I_{12}^2 R_{12}+I_{23}^2 R_{23}= (2\,\mathrm{A})^2 (6\,\Omega)+(0.5\,\mathrm{A})^2(6\,\Omega)= 25.5\,\mathrm{W}$

o como

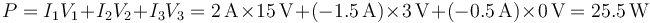
$P=I_1V_1+I_2V_2+I_3V_3 = 2\,\mathrm{A}\times 15\,\mathrm{V}+(-1.5\,\mathrm{A})\times 3\,\mathrm{V}+(-0.5\,\mathrm{A})\times 0\,\mathrm{V} = 25.5\,\mathrm{W}$

5.3 Pregunta 3

¿Cuánta energía hay almacenada en el condensador?

A 112.5nJ
B 0J
C 225nJ
D No hay suficiente información para saberlo.

Solución

La respuesta correcta es la A.

Puesto que por esa rama no circula corriente, en esa resistencia no hay caída de tensión y por tanto, la diferencia de potencial entre las placas del condensador es 15V. Por tanto la energía almacenada vale

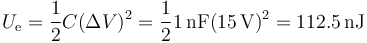
$U_\mathrm{e}=\frac{1}{2}C(\Delta V)^2 =\frac{1}{2}1\,\mathrm{nF}(15\,\mathrm{V})^2=112.5\,\mathrm{nJ}$

6 Calentamiento de agua

Dentro de un recipiente con émbolo móvil se tienen 100 cm³ de agua a 20 °C siendo la presión exterior de 100 kPa. En el agua está sumergida una resistencia eléctrica de 1 kΩ entre cuyos extremos se aplica un voltaje constante de 100 V durante 2 horas.

Datos: Densidad de masa del agua a 100 kPa en el rango 20 °C-100 °C: 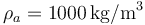$\rho_a=1000\,\mathrm{kg}/\mathrm{m}^3$ ; densidad de masa del vapor de agua a 100 °C y 100 kPa: 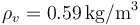$\rho_v=0.59\,\mathrm{kg}/\mathrm{m}^3$ ; temperatura de ebullición del agua a 100 kPa: 99.63 °C; calor específico del agua 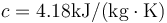$c=4.18 \mathrm{kJ}/(\mathrm{kg}\cdot\mathrm{K})$ ; entalpía específica de vaporización: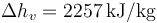 $\Delta h_v=2257\,\mathrm{kJ}/\mathrm{kg}$

6.1 Pregunta 1

¿Cuánto energía se suministra al agua durante el tiempo indicado?

A 72J
B 120kJ
C 120J
D 72kJ

Solución

La respuesta correcta es la D.

La potencia es suministrada por la resistencia eléctrica. De acuerdo con la ley de Joule

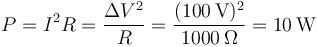
$P=I^2R=\frac{\Delta V^2}{R}=\frac{(100\,\mathrm{V})^2}{1000\,\Omega}=10\,\mathrm{W}$

Como actúa durante dos horas, la energía eléctrica suministrada vale

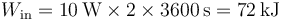
$W_\mathrm{in}=10\,\mathrm{W}\times 2\times 3600\,\mathrm{s}=72\,\mathrm{kJ}$

6.2 Pregunta 2

¿Cuál es la fracción de la masa que se ha convertido en vapor (calidad del vapor de agua) al final del proceso?

A 100%
B 17%
C 0%
D 83%

Solución

La respuesta correcta es la B.

El trabajo eléctrico entra en el agua en forma de calor. Este calor se emplea, en primer lugar, en elevar la tamperatura del agua hasta el punto de ebullición. El calor necesario para ello, es aproximadamente

$Q_1=mc\,\Delta T = 0.1\,\mathrm{kg}\times 4.18\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}\times 80\,\mathrm{K}=33.4\,\mathrm{kJ}$

Puesto que disponemos de 72 kJ, hay calor suficiente para llevar todo el agua al punto de ebullición.

El calor restante se emplea en vaporizar parte del agua. La cantidad de agua que pasa a la fase gaseosa es

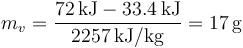
$m_v=\frac{72\,\mathrm{kJ}-33.4\,\mathrm{kJ}}{2257\,\mathrm{kJ}/\mathrm{kg}}=17\,\mathrm{g}$

Puesto que la masa de agua es 100 g, el resultado es una mezcla cuya calidad es del 17%, es decir el 17% está en fase de vapor y el resto en forma líquida.

6.3 Pregunta 3

¿Qué fracción del trabajo eléctrico que ha entrado en el sistema se ha convertido en trabajo de expansión del sistema?

A 4%
B 100%
C 50%
D 96%

Solución

La respuesta correcta es la A.

Cuando el agua pasa de líquido a vapor, su volumen aumenta. Al existir una presión externa constante, esto implica la realización de un trabajo

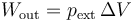
$W_\mathrm{out}=p_\mathrm{ext}\,\Delta V$

El volumen inicial es el del agua, 100 cm³. El final es el del resto del agua, 83 cm³, más el del vapor

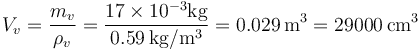
$V_v= \frac{m_v}{\rho_v}=\frac{17\times 10^{-3}\mathrm{kg}}{0.59\,\mathrm{kg}/\mathrm{m}^3}=0.029\,\mathrm{m}^3=29000\,\mathrm{cm}^3$

Vemos que el volumen ocupado por el vapor es muchísimo mayor que el del agua líquida y por tanto para hallar la respuesta correcta podemos ignorar el volumen de líquido. Esto nos da, aproximadamente para el trabajo de expansión

$W_\mathrm{out}\simeq 10^5\,\mathrm{Pa}\times 0.029\,\mathrm{m}^3=2.9\,\mathrm{kJ}$

que, en proporción al trabajo eléctrico es

$\frac{W_\mathrm{out}}{W_\mathrm{in}}=\frac{2.9}{72}=0.04 = 4\%$

7 Condensador con dos capas

Tenemos un condensador de placas planas paralelas que sin relleno tiene una capacidad $C 0$ . Se rellena completamente con dos capas de dieléctrico de igual espesor. Una de ellas tiene permitividad relativa 2.0 y la otra 3.0.

¿Cuánto vale la nueva capacidad del condensador?

A $C = 2.5 C 0$
B $C = 2.4 C 0$
C $C = 5 C 0$
D $C = 4.8 C 0$

Solución

La respuesta correcta es la B.

La capacidad inicial es

$C_0=\frac{\varepsilon_0 S}{b}$

mientras que tras la introducción de los dieléctricos equivale a la de dos condensadores en serie, cada uno de ellos de la mitad de espesor

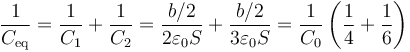
$\frac{1}{C_\mathrm{eq}} = \frac{1}{C_1}+\frac{1}{C_2}=\frac{b/2}{2\varepsilon_0 S}+\frac{b/2}{3\varepsilon_0 S}=\frac{1}{C_0}\left(\frac{1}{4}+\frac{1}{6}\right)$

Invirtiendo las fracciones queda

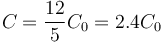
$C=\frac{12}{5}C_0=2.4C_0$

8 Espira que entra en campo magnético

Una espira cuadrada de lado b, resistencia $R$ y autoinducción despreciable se mueve con velocidad constante 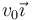$v_0\vec{\imath}$ , paralela a su lado y penetra en un campo magnético uniforme 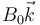$B_0\vec{k}$ que existe en la región 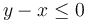$y-x\leq 0$ . En $t = 0$ la esquina del cuadrado penetra en el campo.

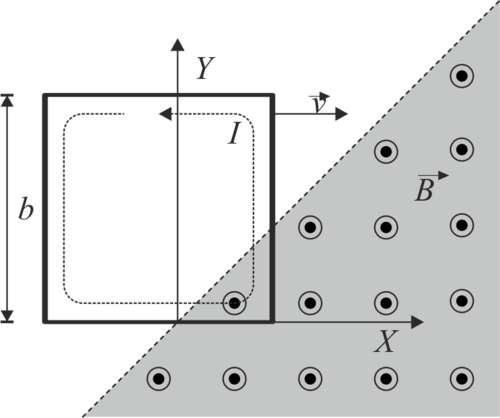
Para $0 < t < b / v 0$ ,

8.1 Pregunta 1

¿cuánto vale la intensidad de corriente, en sentido antihorario, que circula por la espira como función del tiempo?

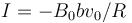
A $I=-B_0 bv_0/R\,$
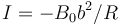
B $I=-B_0 b^2/R\,$
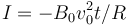
C $I=-B_0 v_0^2 t/R\,$
D $I = 0$

Solución

La respuesta correcta es la C.

Por la ley de Faraday

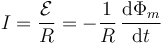
$I=\frac{\mathcal{E}}{R}=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

siendo el flujo magnético el que atraviesa el triángulo de lado $x = v 0 t$

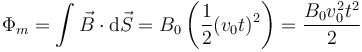
$\Phi_m=\int \vec{B}\cdot\mathrm{d}\vec{S}=B_0\left(\frac{1}{2}(v_0 t)^2\right) = \frac{B_0v_0^2 t^2}{2}$

Derivando aquí respecto al tiempo

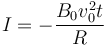
$I= -\frac{B_0v_0^2 t}{R}$

8.2 Pregunta 2

¿cuánto vale la fuerza magnética sobre la espira?

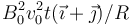
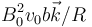
A $B_0^2 v_0^2 t(\vec{\imath}+\vec{\jmath})/R$
B $B_0^2 v_0 b\vec{k}/R$
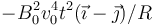
C $-B_0^2 v_0^4 t^2 (\vec{\imath}-\vec{\jmath})/R$
D $\vec{0}$

Solución

La respuesta correcta es la C.

Para una espira parcialmente inmersa en un campo magnético uniforme la fuerza magnética vale

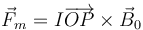
$\vec{F}_m=I\overrightarrow{OP}\times\vec{B}_0$

siendo P el punto en el que la espira entra en el campo magnético y B en el que sale. Esto da

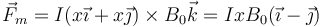
$\vec{F}_m=I(x\vec{\imath}+x\vec{\jmath})\times B_0\vec{k}=IxB_0(\vec{\imath}-\vec{\jmath})$

Sustituyendo el valor de $x = v 0 t$ y la intensidad calculada en la pregunta anterior llegamos a la respuesta.

9 Proceso adiabático

En cualquier proceso adiabático que lleve a un sistema desde un estado A a uno B, prefijados,…

A la temperatura permanece constante.
B la energía interna permanece constante.
C el trabajo realizado es independiente del camino.
D la entropía del sistema permanece constante.

Solución

La respuesta correcta es la C.

De acuerdo con el primer principio de la termodinámica, para un proceso adiabático,

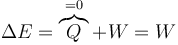
$\Delta E = \overbrace{Q}^{=0}+W = W$

Puesto que la energía total es una función de estado, esto implica que el trabajo en este proceso no depende del camino.

La entropía no permanece constante porque el proceso puede ser irreversible.

Tampoco es constante la temperatura, ya que el proceso en general no será isotermo. Por tanto, tampoco será constante la energía interna, que depende principalmente de la temperatura.

10 Trabajo perdido

Una máquina térmica que toma un calor $Q in$ de un foco caliente a $T C$ y expulsa $Q out$ a un foco frío a $T F$ siempre pierde una cierta cantidad de trabajo respecto al máximo posible. ¿Cuánto vale éste trabajo perdido?

A $Q out$
B $Q in - Q out$
C $Q out - (T F / T C) Q in$
D $Q in - (T F / T C) Q out$

Solución

La respuesta correcta es la C.

Véase el apartado correspondiente en la teoría.

11 Dilatación de esfera

Se tiene una esfera hueca de cobre, cuyo radio interior es de 5.0cm, el exterior de 6.0cm y que se encuentra a 20 °C. Se calienta el metal hasta 80 °C, siendo el coeficiente de dilatación lineal del cobre $\alpha =16.6\times 10^{-6} \mathrm{K}^{-1}$ . ¿En qué proporción varía el volumen del hueco esférico?

A Aumenta un 0.3%.
B Disminuye un 0.1%.
C Aumenta un 0.1%.
D Disminuye un 0.3%.

Solución

La respuesta correcta es la A.

Cuando un material se dilata sus átomos se separan, lo cual implica que el tamaño del hueco aumentará.

El coeficiente de dilatación volumétrico es igual al triple del lineal

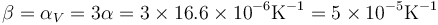
$\beta = \alpha_V = 3\alpha = 3\times 16.6\times 10^{-6}\mathrm{K}^{-1}=5\times 10^{-5}\mathrm{K}^{-1}\,$

Esto da un aumento relativo del volumen

$\frac{\Delta V}{V}=\beta\,\Delta T = 5\times 10^{-5}\times 60 =3\times 10^{-3}=0.3\%$

Test de la Segunda Convocatoria 2015-2016

De Laplace

Contenido

1 Dipolo en campo eléctrico

2 Propiedades del equilibrio electrostático

3 Efecto de un campo magnético variable

4 Campo de dos superficies esféricas

5 Circuito triangular

5.1 Pregunta 1

5.2 Pregunta 2

5.3 Pregunta 3

6 Calentamiento de agua

6.1 Pregunta 1

6.2 Pregunta 2

6.3 Pregunta 3

7 Condensador con dos capas

8 Espira que entra en campo magnético

8.1 Pregunta 1

8.2 Pregunta 2

9 Proceso adiabático

10 Trabajo perdido

11 Dilatación de esfera

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES