Sistemas de partículas
De Laplace
Contenido |
1 Definición de sistema de partículas
En mecánica consideramos un sistema de partículas como un conjunto de N puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas.
Cada una de las partículas del sistema posee una masa propia, mi, siendo 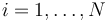 un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición
un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición 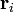 y una velocidad
y una velocidad 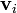 . Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica
. Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica
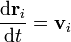
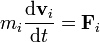
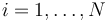
siendo 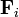 la resultante de las fuerzas que actúan sobre la partícula i. Esta resultante se compone de las fuerzas que cada una de las demás partículas del sistema ejerce sobre i, más la resultante de las fuerzas externas aplicadas sobre ella
la resultante de las fuerzas que actúan sobre la partícula i. Esta resultante se compone de las fuerzas que cada una de las demás partículas del sistema ejerce sobre i, más la resultante de las fuerzas externas aplicadas sobre ella
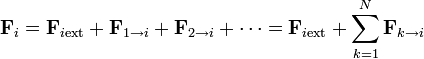
Este sumatorio representa la suma sobre las partículas restantes, esto es k va de 1 hasta N, excluyendo el caso k = i, ya que admitimos que una partícula no produce fuerza sobre sí misma (equivalentemente, 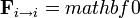 ).
).
Suponemos que las interacciones entre las partículas obdecen la 3ª ley de Newton
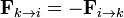
o, lo que es lo mismo
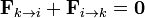
En la mayoría de los casos se cumplirá además que la fuerza que la partícula k ejerce sobre la i (y por tanto la que la i ejerce sobre la k) va en la dirección de la recta que une ambas partículas. Matemáticamente, esto se expresa imponiendo que el vector 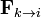 es paralelo a la posición relativa
es paralelo a la posición relativa 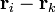 , esto es, si
, esto es, si
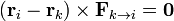
Eliminando paréntesis y aplicando la tercera ley de Newton esto equivale a la condición
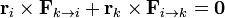
2 Propiedades de un sistema de partículas
Un sistema de partículas puede contener 2 o 3 partículas, pero también muchos miles de millones de ellas (por ejemplo 1 cm³ de agua contiene 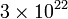 moléculas, cada una de las cuales contiene 26 partículas, entre protones, neutrones y electrones). Por ello, en la mayoría de los casos no es posible estudiar un sistema de partículas a partir de la evolución de cada uno de las partículas que lo forman (entre otras cosas, porque desconocemos la posición y la velocidad exacta de cada una).
moléculas, cada una de las cuales contiene 26 partículas, entre protones, neutrones y electrones). Por ello, en la mayoría de los casos no es posible estudiar un sistema de partículas a partir de la evolución de cada uno de las partículas que lo forman (entre otras cosas, porque desconocemos la posición y la velocidad exacta de cada una).
En su lugar, nos restringimos a considerarlas colectivamente, definiendo propiedades del conjunto, que cumplen sus propias leyes de evolución. Esta reducción es particularmente útil en el caso del sólido rígido, para el cual las magnitudes que vamos a definir a continuación son suficientes para determinar la evolución del sistema completo.
2.1 Masa total
La masa total del sistema es la suma de las masas de los partículas que lo componen
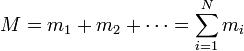
2.1.1 Densidad de masa
Cuando tenemos un sistema de muchos millones de partículas (como en un sólido, o un fluido), no es práctico hacer el sumatorio de las masas individuales. En su lugar se divide el sistema en elementos de volumen, Δτ, que son regiones del espacio lo suficientemente pequeñas para tratarlas como diferenciales, pero lo suficientemente grandes como para que contengan miles de partículas. El sistema se considera entonces como continuo, esto es, en lugar de describirse como formado por partículas separadas, se considera constituido por elementos de volumen adyacentes.
Se define entonces la densidad de masa, ρ de un elemento de volumen, como la masa de las partículas que lo forman, dividida por el volumen del elemento
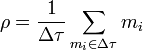
Dicho de otra forma, la masa de un elemento de volumen es el producto de la densidad de masa por el volumen del elemento
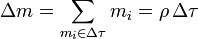
La masa total del sistema será la suma de la masa de todos sus elementos

Una suma de muchas cantidades muy pequeñas no es otra cosa que una integral
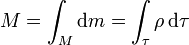
Aquí la densidad es una función de la posición porque en un sistema no homogéneo (por ejemplo, el cuerpo humano) la densidad varía de un punto a otro.
2.2 Centro de masas
El centro de masas (CM) de un sistema de partículas es una media ponderada, según la masa individual, de las posiciones de todas las partículas que lo componen
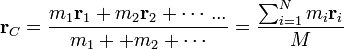
Equivalentemente se cumple
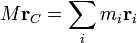
En el caso de un sistema continuo, habrá que sumar para todos los elementos que lo componen
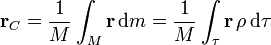
2.2.1 Velocidad del centro de masas
El centro de masas no es un punto fijo, sino que puede desplazarse cuando lo hacen las partículas del sistema. Obtenemos su velocidad derivando la definición respecto al tiempo
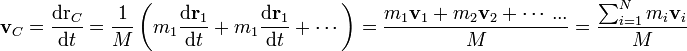
2.2.2 Posición relativa al centro de masas
Una vez definida la posición del centro de masas, interesa indicar dónde están situadas las partículas respecto al CM. Esto se consigue definiendo la posición relativa
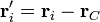
De manera análoga se define la velocidad relativa al CM
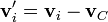
2.3 Cantidad de movimiento
La cantidad de movimiento (o momento lineal) del sistema es la suma de las cantidades de movimiento de cada una de las partículas
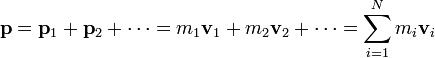
La cantidad de movimiento se relaciona directamente con el centro de masas del sistema. Derivando respecto al tiempo la relación
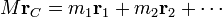
obtenemos
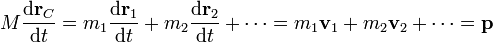
esto es
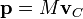
En palabras: la cantidad de movimiento del sistema equivale a la que tendría una sola partícula material que concentrara toda la masa del sistema y que se moviera como el centro de masas de éste.
De la relación entre cantidad de movimiento y centro de masas se llega a que la cantidad de movimiento del sistema respecto al centro de masas es siempre nula
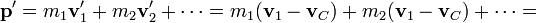
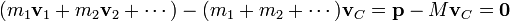
Esto permite redefinir el centro de masas como aquel punto (variable) desde el cual la cantidad de movimiento del sistema es nula en todo momento. Cuando un sistema de partículas se estudia empleando este punto como origen del sistema de referencia se dice que se está estudiando desde el sistema centro de masas.
2.4 Momento angular (o cinético)
De manera análoga a la cantidad de movimiento, se define el momento cinético (o angular) de un sistema de partículas como la suma vectorial de los momentos cinéticos individuales
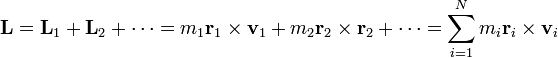
2.4.1 Descomposición del momento angular
Las ecuaciones de la dinámica de sistemas se simplificarían notablemente si el momento angular, como el lineal, equivaliera al de una partícula puntual que concentrara toda la masa. No es así.
Para relacionar el momento angular con el centro de masa, descomponemos cada posición y cada velocidad en suma de la del centrode masa más la posición o velocidad relativas
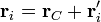
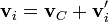
Con esta descomposición, el momento angular de cada partícula se separa en cuatro términos
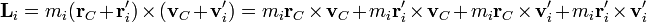
Al sumar los momentos cinéticos individuales para obtener el momento angular total nos quedan cuatro sumas, en cada una de las cuales podemos sacar factor común la posición o la velocidad del CM, que es una cantidad que no depende del índice i
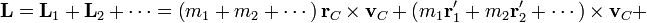
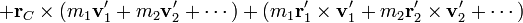
Ahora bien, de la definición de centro de masas se deduce que
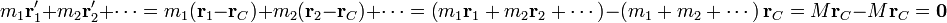
y, del mismo modo,
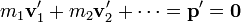
Por tanto, el segundo y el tercer término en la expresión del momento cinético total se anulan y la expresión se reduce a
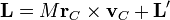
donde
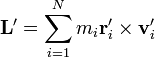
es el momento angular relativo al centro de masas.
Según esto, el momento angular o cinético de un sistema de partículas se compone de dos contribuciones: el momento angular que tendría una partícula que contuviera toda la masa y se moviera como el centro de masas del sistema, más el momento angular que tienen las partículas por moverse alrededor del centro de masas.
Un ejemplo físico sencillo de esta descomposición lo tenemos en el momento angular de la Tierra en cuanto planeta del Sistema Solar. Su momento angular se compone de una parte debida al movimiento de traslación alrededor del Sol (lo que se conoce como momento angular orbital), que sería el primer término, más otra parte debida al movimiento de rotación alrededor de su eje (el llamado momento angular intrínseco), que sería 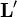 .
.
2.5 Energía cinética
La energía cinética del sistema es la suma escalar de las energías cinéticas individuales
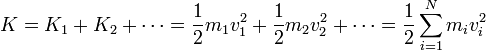
2.5.1 Descomposición de la energía cinética
Para la energía cinética podemos efectuar una descomposición análoga a la del momento cinético. Escribiendo cada velocidad como suma de la del CM más la relativa
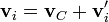
queda, para la energía cinética individual,
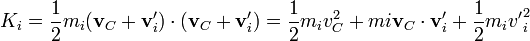
y para la energía cinética total
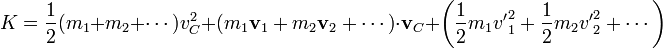
El segundo término se anula por aparecer en él 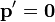 , lo que reduce la energía cinética a
, lo que reduce la energía cinética a
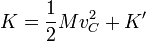
con
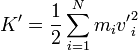
la energía cinética del sistema relativa al centro de masas.
Esta descomposición se interpreta como que el sistema posee una energía cinética por el movimiento de traslación colectivo, más un término debido al movimiento sobre sí mismo. Esta energía cinética intrínseca, K' es parte de la energía interna del sistema. Puede estar asociada a:
- un movimiento organizado. Por ejemplo, en la rotación de la Tierra alrededor de su eje.
- un movimiento desorganizado. Por ejemplo, en un gas que se encuentra a una cierta temperatura, el centro de masas puede estar estacionario y sin embargo el gas posee una energía cinética debido al movimiento de las moléculas que lo componen. Esta energía cinética es lo que llamamos agitación térmica.
- una combinación de ambos. Este es el caso general. La energía cinética del sistema parte se encuentra en movimientos macroscópicos (rotación o traslación de partes del sistema) y parte en movimientos microscópicos caóticos.
Por la presencia de estos términos microscópicos caóticos la energía cinética total del sistema es normalmente desconocida. En su lugar nos limitamos a la suma del término 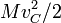 con la suma de las energías cinéticas debidas a los movimientos macroscópicos.
con la suma de las energías cinéticas debidas a los movimientos macroscópicos.
3 Leyes de conservación
La utilidad de las definiciones del centro de masa y las propiedades colectivas del sistema se pone de manifiesto cuando se estudia cómo varían en el tiempo y en qué casos son constantes de movimiento.
3.1 De la cantidad de movimiento
Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es
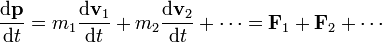
esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas
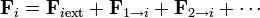
y la derivada de la cantidad de movimiento queda
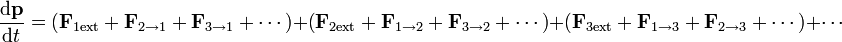
Pero, de acuerdo con la tercera ley de Newton
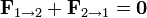
y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil
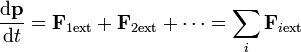
esto es:
- la derivada de la cantidad de movimiento es igual a la resultante de las fuerzas externas aplicadas sobre el sistema.
- En particular: En ausencia de fuerzas externas, la cantidad de movimiento de un sistema de partículas permanece constante.
En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe
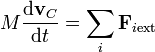
es decir:
- El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se ecnontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema.
- En particular, el centro de masas de un sistema de partículas sometidas exclusivamente a fuerzas internas permanece en reposo o en un estado de movimiento uniforme.
Consideremos el ejemplo siguiente: un proyectil se lanza desde un mortero. El proyectil describe (despreciando la resistencia del aire) una trayectoria parabólica. En cierto punto del vuelo el proyectil explota en multitud de fragmentos. El centro de masas de estos fragmentos continúa el movimiento parabólico inicial.
Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide.
3.2 Del momento angular
Derivando igualmente en la expresión del momento cinético de un sistema de partículas obtenemos
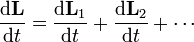
Para cada partícula la derivada del momento angular es el momento de las fuerzas aplicadas sobre ella:
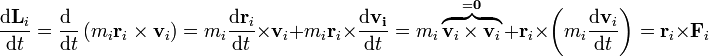
y, para el momento cinético total
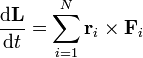
De nuevo, esta expresión requiere conocer las fuerzas internas del sistema, que son usualmente desconocidas. Por ello, descomponemos de nuevo en sumas de fuerzas externas e internas
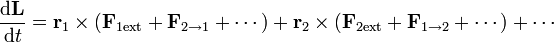
Pero, según dijimos al principio del artículo, si las fuerzas internas entre dos partículas no solo cumplen la tercera ley de Newton, sino que además son centrales, esto es, van en la dirección de la recta que une las dos partículas se verifica
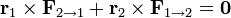
Esta condición se cumple en la mayoría de los casos prácticos (fuerzas eléctricas o gravitatorias). En este caso, los momentos de las fuerzas internas se anulan dos a dos y queda
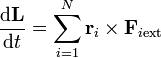
En palabras:
- La derivada del momento angular o cinético de un sistema de partículas es igual a la suma de los momentos de las fuerzas externas aplicadas sobre el sistema.
- En particular, en un sistema de partículas sometido exclusivamente a fuerzas internas, el momento angular permanece constante.
3.3 El caso de la energía cinética
Para la energía cinética no existe un teorema tan simple como para la cantidad de movimiento o el momento cinético. Operando del mismo modo que para estas dos cantidades, en sencillo probar que
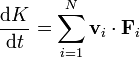
esto es, la derivada de la energía cinética es la potencia desarrollada por todas las fuerzas ejercidas en el sistema. Sin embargo, en este caso, no podemos eliminar las fuerzas internas de la ecuación. La razón es que las fuerzas internas sí pueden variar la energía cinética total.
Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total.
4 Aplicaciones
4.1 Sistema de dos partículas
4.1.1 Explosión de un proyectil
Supongamos un proyectil de masa M que es disparado con un mortero desde el suelo. Cuando el proyectil lleva recorrida horizontalmente una distancia a y se encuentra en el punto más alto de la parábola, se parte en dos pedazos desiguales. Uno de ellos, de masa M / 3 cae justo en la vertical del punto de explosión. El segundo fragmento impacta en el suelo al mismo tiempo que el primero. ¿A qué distancia del primero?
Una forma de resolver esto sería determinar la velocidad del segundo fragmento inmediatamente tras la explosión y estudiar su movimiento parabólíco siguiente, para hallar su alcance, pero no se nos dice ni la velocidad inicial, ni el ángulo con que fue disparado el proyectil.
Lo más sencillo es utilizar que el centro de masas se mueve como una partícula sometida a la resultante de las fuerzas externas, en este caso, el peso total. Por tanto, describe el arco de parábola completo, hasta impactar en el suelo, a una distancia 2a del punto del disparo.
Si el fragmento de masa M / 3 se encuentra en x1 = a y el centro de masas en xC = 2a, ambos a la altura y = 0, la posición del segundo fragmento la obtenemos de
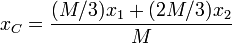
 3xC = x1 + 2x2
3xC = x1 + 2x2  6a = a + 2x2
6a = a + 2x2 
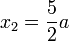
4.1.2 Dos partículas unidas por un oscilador armónico
Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad v0 alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?
4.1.3 Dos partículas unidas por una barra
Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que puden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v0 perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?





