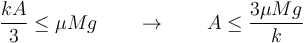Rodillo unido a un resorte
De Laplace
Contenido |
1 Enunciado
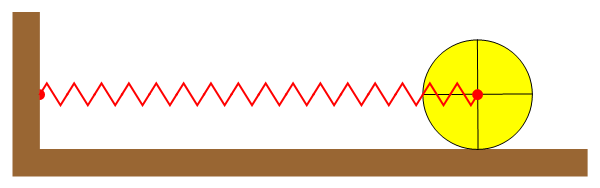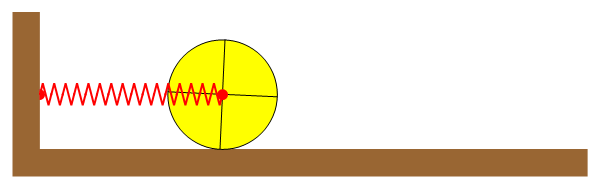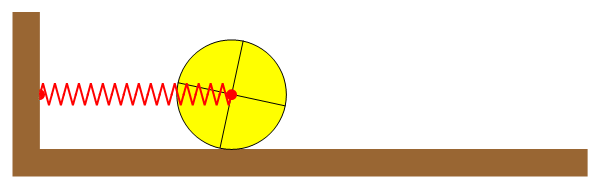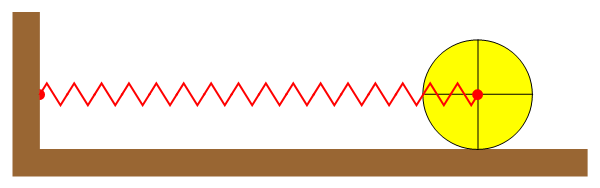
Un rodillo cilíndrico macizo de radio R y masa M se encuentra apoyado sobre una superficie horizontal, siendo el coeficiente de rozamiento (estático y dinámico) μ. El eje del rodillo está atado a la pared mediante un resorte de constante k y longitud natural l0.
Se separa el rodillo de la posición de equilibrio una distancia A y se suelta desde el reposo. El rodillo rueda sin deslizar.
- Halle la velocidad del centro del rodillo y la velocidad angular para el instante en que su centro pasa por la posición de equilibrio.
- ¿Cuánto vale el periodo de las oscilaciones que describe?
- Calcule la fuerza de rozamiento estático que ejerce el suelo sobre el rodillo (a) en la posición inicial y (b) al pasar por la posición de equilibrio.
- ¿Cuál es el máximo valor de A que se puede alejar el rodillo si no se quiere que este empiece a deslizar sobre el suelo?
2 Introducción
Este problema es muy similar al de una bola que rueda por una pendiente, con la diferencia de que allí la fuerza que hace rodar la bola es el peso y aquí el rodillo rueda por la fuerza elástica.
3 Velocidades
Este apartado se puede hacer de forma sencilla tanto empleando el balance energético como el de las fuerzas aplicadas.
3.1 Mediante el balance de energía
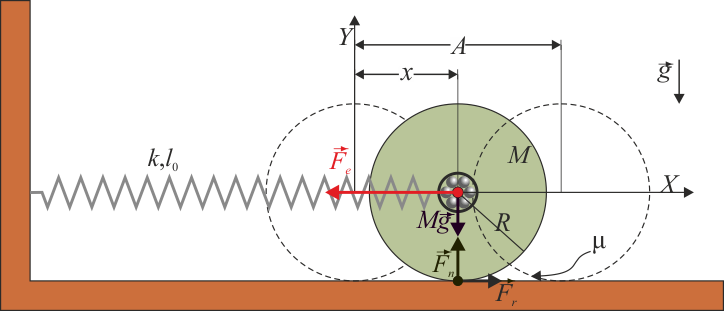
Sobre el rodillo actúan cuatro fuerzas:
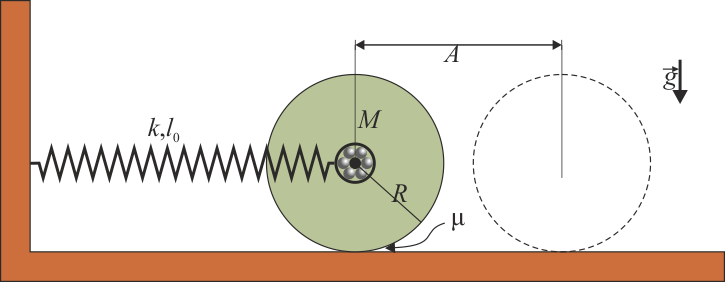
- Su peso, que es vertical y constante.
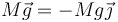
- La reacción normal del suelo, que dado que no hay desplazamiento vertical, va a ser siempre opuesta al peso.
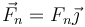
- La fuerza elástica, que verifica la ley de Hooke
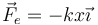
- La fuerza de rozamiento estático, que es la que consigue que el cilindro ruede sin deslizar
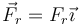
De estas cuatro fuerzas, las dos aplicadas en el punto de contacto, 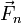 y
y  , no desarrollan potencia alguna, por ser nula la velocidad de este punto. Las otras dos, el peso y la fuerza elástica, son fuerzas conservativas.
, no desarrollan potencia alguna, por ser nula la velocidad de este punto. Las otras dos, el peso y la fuerza elástica, son fuerzas conservativas.
Por tanto, se conserva la energía mecánica en este sistema.
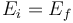
La energía mecánica inicial es solo potencial, ya que el cilindro parte del reposo
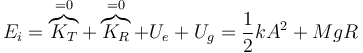
La energía, cuando pasa por la posición de equilibrio contiene energía cinética de rotación, de traslación y mantiene potencial gravitatoria, ya que no ha subido ni bajado.
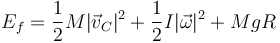
Igualando las dos cantidades queda
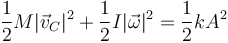
Queda relacionar las energías cinéticas de rotación y traslación. Por ser un cilindro macizo
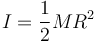
y, por estar rodando sin deslizar, las velocidades tienen las direcciones y sentidos

(en realidad la velocidad va a ir en sentido de x decreciente, pero esto no afecta a esta expresión, simplemente vC < 0) cumpliéndose
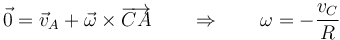
Por tanto, la energía cinética de rotación es igual a
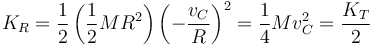
Sustituyendo en la ley de conservación de la energía mecánica queda
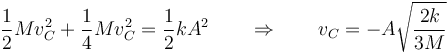
y para la velocidad angular
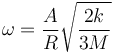
En forma vectorial

3.2 Mediante el análisis de fuerzas
El análisis es idéntico al caso general de rodadura con fuerza aplicada, siendo en esta caso la fuerza aplicada la elástica
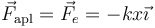
de forma que las ecuaciones de movimiento para el sólido son
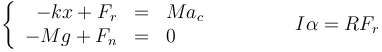
donde
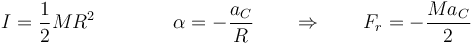
lo que permite eliminar la fuerza de rozamiento estático

Esta es la ecuación de un oscilador armónico de frecuencia

Puesto que el estado inicial es en reposo en x = A, la solución de esta ecuación de movimiento es
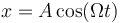
siendo la velocidad
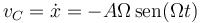
En la posición de equilibrio el seno vale la unidad y la velocidad se reduce a
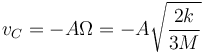
con la velocidad angular
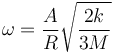
En forma vectorial

4 Periodo de oscilación
Este apartado se puede hacer también por balance energético y por análisis de fuerzas, aunque es mucho más sencillo por el segundo método.
Puesto que hemos deducido que el centro de masas cumple la ecuación del oscilador armónico

entonces el periodo de oscilación es
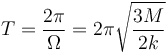
Nótese que el periodo de oscilación no se relaciona directamente con la velocidad angular con que gira el rodillo. Una cosa es el periodo de oscilación de un m.a.s. y otra el periodo de revolución en un movimiento de rotación.
5 Fuerza de rozamiento estático
Tal como vimos antes, para cualquier posición del rodillo
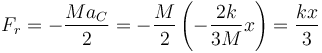
En la posición inicial
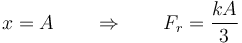
y en la de equilibrio, en la que el resorte no hace fuerza
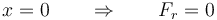
En forma vectorial
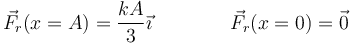
6 Amplitud máxima
La condición para que no se produzca deslizamiento es que la fuerza de rozamieno estático no supere su valor límite

lo que nos da la condición