Bola que rueda por una pendiente

De Laplace

Contenido

1 Enunciado
2 Introducción
3 Relación entre aceleraciones
4 Energías
5 Aceleración
- 5.1 A partir de las fuerzas
- 5.2 A partir de la energía
6 Coeficiente de rozamiento mínimo

1 Enunciado

Una esfera metálica de acero con radio 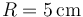$R=5\,\mathrm{cm}$ ) se encuentra inicialmente en reposo a una altura 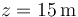$z=15\,\mathrm{m}$ y desciende rodando sin deslizar por el plano inclinado con un ángulo 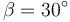$\beta=30^\circ$ . El coeficiente de rozamiento estático entre el plano y el cilindro es $μ$ . El rozamiento por rodadura es despreciable.

¿Qué relación existe entre la aceleración angular de la esfera y la lineal de su centro de masas?
¿Cuánto valen la energía cinética de rotación, la cinética de traslación, la potencial (tomando $z = 0$ como referencia) y la mecánica cuando se halla en $z=5\,\mathrm{m}$ ?
¿Cuánto vale, en módulo, la aceleración lineal del centro de masas de la esfera?
¿Cuál es el valor mínimo que debe tener el coeficiente de rozamiento $μ$ si la esfera rueda sin deslizar?

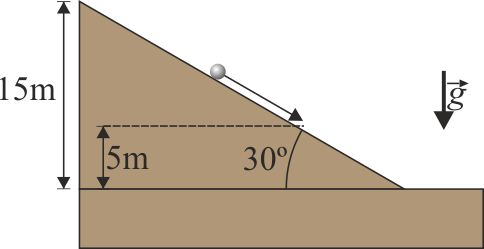
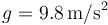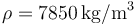Dato: Momento de inercia de una esfera de masa $M$ y radio $R$ respecto a un eje que pasa por su centro: $I = (2 / 5) M R 2$ . Aceleración de la gravedad $g = 9.8\,\mathrm{m}/\mathrm{s}^2$ . Densidad de masa del acero: $\rho = 7850\,\mathrm{kg}/\mathrm{m}^3$ .

2 Introducción

Este problema es una consecuencia inmediata de lo que se discute en teoría sobre rodadura, siendo en este caso la fuerza aplicada la componente útil del peso (la tangencial al plano).

3 Relación entre aceleraciones

Elegimos un sistema de ejes en el que el eje OX es el tangencial al plano en la dirección de descenso (contando x desde el punto de partida), OY el normal al plano hacia fuera de él y OZ el perpendicular a la figura y en el sentido hacia afuera de ésta (o de la pantalla).

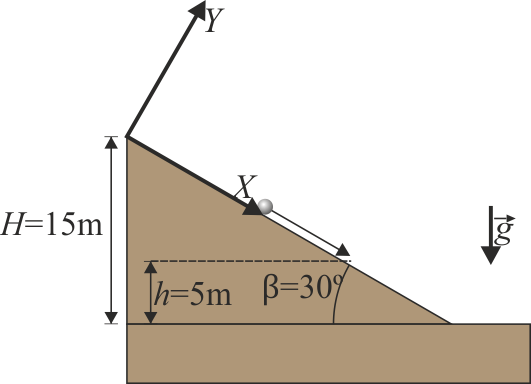
En este sistema, la velocidad y la aceleración del CM es en la dirección de movimiento, es decir

$\vec{v}_C=v_C\vec{\imath}\qquad\qquad \vec{a}_C = a_C\vec{\imath}$

mientras que la velocidad y la aceleración angular son perpendiculares al plano de la figura

$\vec{\omega}=\omega\vec{k}\qquad \vec{\alpha}=\alpha\vec{k}$

Por estar rodando sin deslizar, se anula la velocidad del punto A de contacto entre la bola y el suelo.

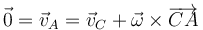
$\vec{0}=\vec{v}_A=\vec{v}_C+\vec{\omega}\times\overrightarrow{CA}$

siendo

$\overrightarrow{CA}=-R\vec{\jmath}$

sustituyendo en la expresión anterior llegamos a la relación escalar

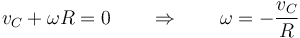
$v_C+\omega R = 0\qquad\Rightarrow\qquad \omega = -\frac{v_C}{R}$

y derivando en esta expresión

$\alpha = -\frac{a_C}{R}$

Esta es una relación escalar entre componentes. Los vectores tienen direcciones diferentes

$\vec{a}_C=a_C\vec{\imath}\qquad\qquad \vec{\alpha}=-\frac{a_C}{R}\vec{k}$

Para nuestro caso concreto, empleando el SI, queda la relación

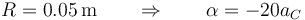
$R = 0.05\,\mathrm{m}\qquad\Rightarrow\qquad \alpha = -20a_C$

4 Energías

Las únicas fuerzas que actúan sobre la esfera son su peso (que es una fuerza conservativa) y la de rozamiento estático, que no realiza trabajo por ser nula la velocidad del punto de contacto.

Esto quiere decir que en este sistema se conserva la energía mecánica

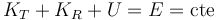
$K_T+K_R+U = E=\mathrm{cte}\,$

Inicialmente, la esfera está en reposo a una altura H = 15 m, por lo que el valor de la energía mecánica es en todo momento

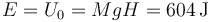
$E = U_0 = MgH = 604\,\mathrm{J}$

siendo la masa

$M = \rho V = \frac{4\pi}{3}R^3=4.11\,\mathrm{kg}$

Cuando está a una altura h = 5 m, la energía potencial se ha reducido a

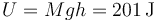
$U = M g h = 201\,\mathrm{J}$

y el resto de la energía mecánica se ha ido en energía cinética. Para ver cómo se reparte entre energía de rotación y de traslación observamos que

$K_T = \frac{1}{2}M|\vec{v}_C|^2\qquad\qquad K_R = \frac{1}{2}I|\vec{\omega}^2$

Estas dos cantidades se relacionan observando que para una esfera que rueda

$I = \frac{2}{5}MR^2\qquad\qquad |\vec{\omega}|=\frac{|\vec{v}_C|}{R}$

y por tanto

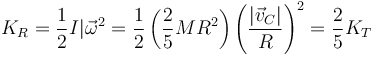
$K_R = \frac{1}{2}I|\vec{\omega}^2= \frac{1}{2}\left(\frac{2}{5}MR^2\right)\left(\frac{|\vec{v}_C|}{R}\right)^2 = \frac{2}{5}K_T$

Llevando esto a la ley de conservación de la energía mecánica

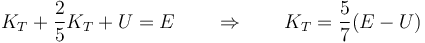
$K_T + \frac{2}{5}K_T + U = E\qquad\Rightarrow\qquad K_T = \frac{5}{7}(E-U)$

siendo su valor numérico

$K_T = \frac{5}{7}(604-201)\,\mathrm{J}= 288\,\mathrm{J}$

La energía cinética de rotación es proporcional a ésta, según acabamos de ver

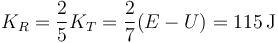
$K_R = \frac{2}{5}K_T = \frac{2}{7}(E-U) = 115\,\mathrm{J}$

5 Aceleración

Las aceleraciones (la del CM y la angular) las podemos hallar por el análisis de las fuerzas o por el de la energía.

5.1 A partir de las fuerzas

El análisis es idéntico al discutido en teoría para la rodadura con fuerza aplicada.

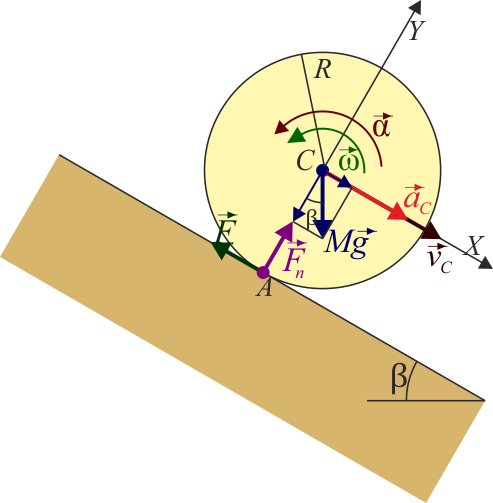
Sobre la bola actúan dos fuerzas:

El peso

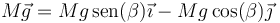
$M\vec{g}=Mg\,\mathrm{sen}(\beta)\vec{\imath}-Mg\cos(\beta)\vec{\jmath}$

La fuerza en el punto de contacto; la cual se compone a su vez de una fuerza de reacción normal y de una fuerza de rozamiento estático

$\vec{F}=\vec{F}_r + \vec{F}_n = -F_r\vec{\imath}+F_n\vec{\jmath}$

Vemos que, en este caso, la fuerza aplicada es la componente del peso en la dirección tangencial al plano

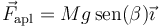
$\vec{F}_\mathrm{apl}=Mg\,\mathrm{sen}(\beta)\vec{\imath}$

Las leyes de la dinámica para el sólido nos dan para las fuerzas, separando por componentes

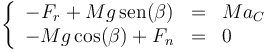
$\left\{\begin{array}{rcl} -F_r +Mg\,\mathrm{sen}(\beta)& = & Ma_C \\ -Mg\cos(\beta)+F_n & = & 0 \end{array}\right.$

y para los momentos

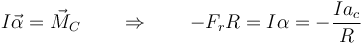
$I\vec{\alpha}=\vec{M}_C\qquad\Rightarrow\qquad -F_rR=I\alpha=-\frac{Ia_c}{R}$

La solución de este sistema es, para la aceleración lineal

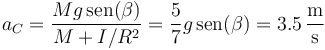
$a_C=\frac{Mg\,\mathrm{sen}(\beta)}{M+I/R^2}=\frac{5}{7}g\,\mathrm{sen}(\beta)=3.5\,\frac{\mathrm{m}}{\mathrm{s}}$

Para la angular

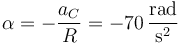
$\alpha = -\frac{a_C}{R}=-70\,\frac{\mathrm{rad}}{\mathrm{s}^2}$

y para la fuerza de rozamiento estático

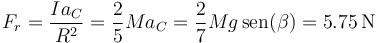
$F_r = \frac{Ia_C}{R^2}=\frac{2}{5}Ma_C = \frac{2}{7}Mg\,\mathrm{sen}(\beta) = 5.75\,\mathrm{N}$

En forma vectorial, cada una de estas tres cantidades tienen las direcciones indicandas anteriormente

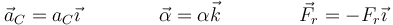
$\vec{a}_C = a_C\vec{\imath}\qquad\qquad \vec{\alpha}=\alpha\vec{k}\qquad\qquad \vec{F}_r=-F_r\vec{\imath}$

5.2 A partir de la energía

Antes dedujimos que, para cualquier instante se cumple

$K_T + K_R + U = E\qquad\qquad K_R = \frac{2}{5}K_T$

Sustituyendo aquí las diferentes expresiones queda

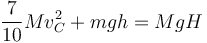
$\frac{7}{10}Mv_C^2 + mgh = MgH$

Si aquí derivamos respecto al tiempo, obtenemos

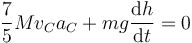
$\frac{7}{5}Mv_Ca_C + mg\frac{\mathrm{d}h}{\mathrm{d}t}=0$

La cantidad dh/dt mide como aumenta h con el tiempo. Aplicando que

$h = H - x\,\mathrm{sen}(\beta)\qquad\Rightarrow\qquad \frac{\mathrm{d}h}{\mathrm{d}t}=-v_C\,\mathrm{sen}(\beta)$

obtenemos

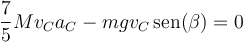
$\frac{7}{5}Mv_Ca_C - mgv_C\,\mathrm{sen}(\beta)=0$

y despejamos

$a_C = \frac{5}{7}g\,\mathrm{sen}(\beta)$

De aquí podemos calcular ahora la aceleración angular. Desgraciadamente, este método no nos da de forma inmediata la fuerza de rozamiento.

6 Coeficiente de rozamiento mínimo

Antes hemos visto que, de las leyes de la dinámica obteníamos los valores de las fuerzas en el punto de contacto

$F_r = \frac{2}{7}Mg\,\mathrm{sen}(\beta)\qquad \qquad F_n = Mg\cos(\beta)$

Para que no haya deslizamiento debe cumplirse que la fuerza de rozamiento esté por debajo de su valor límite

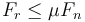
$F_r\leq \mu F_n\,$

lo que nos da

$\frac{2}{7}Mg\,\mathrm{sen}(\beta) \leq \mu Mg\cos(\beta)\qquad\Rightarrow\qquad \mu > \frac{2}{7}\mathrm{tg}(\beta) = 0.165$

Por debajo de este coeficiente de fricción, la bola empezaría a patinar.

Bola que rueda por una pendiente

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Relación entre aceleraciones

4 Energías

5 Aceleración

5.1 A partir de las fuerzas

5.2 A partir de la energía

6 Coeficiente de rozamiento mínimo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES